前言

什么是斐波那契数列？

斐波那契数列的提出者，是意大利数学家列昂纳多·斐波那契（Leonardo Fibonacci），生于公元1170年，卒于1250年，籍贯是比萨。他被人称作“比萨的列昂纳多”。当年斐波纳契数列是斐波那契以兔子繁殖的案例引入，所以也称为兔子数列，指的是这样一个数组：0,1,1,2,3,5,8,13,21,34,55,89,144,233,377......

斐波那契数列又称黄金分割数列，是不是听到黄金分割就觉的很高大上，的确斐波那契数列应用领域很广泛很高大上，特别是在现代物理，准晶体结构、化学等领域，斐波那契数列都有直接的应用。为此，美国数学会从1963起出版了以《斐波那契数列季刊》为名的一份数学杂志，用于专门刊载这方面的研究成果。由此可见斐波那契数列的重要性

在数学上,斐波纳契数列被以递归的方法定义：F（0）=0，F（1）=1，F（n）=F(n-1)+F(n-2)（n≥2，n∈N*），在编程实现中，递归也是常用于实现斐波那契数列的求解。下图仅为fibo(3)一项的计算:

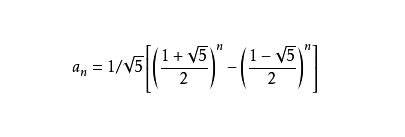
上图为通项公式，又称为“比内公式”，是用无理数表示有理数的一个范例。

注：此时a1=1，a2=1，an=a(n-1)+a(n-2)（n>=3,n∈N*）

下图为通项公式的推导式：利用特征方程（线性代数解法）

线性递推数列的特征方程为：

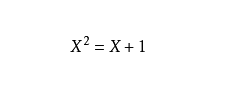
下面为推导过程，解得

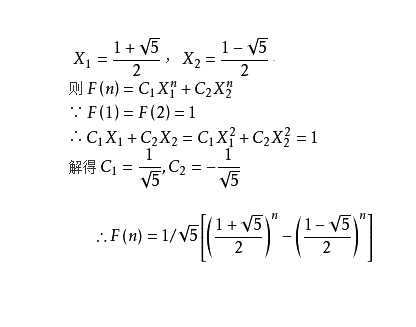
涉及到的Python知识点

序列

在数学中，序列称为数列。是指按照一定顺序排列的一列数字，比如斐波那契数列。在Python编程中，序列是最基本的数据结构，是用于存放多个连续内存空间，并且按一定顺序排列，每一个值都分配一个数字，这个数字被称为索引，我们可以通过该索引取出相应的值。Python存在5个常用的序列结构，分别为：列表，元组，集合，字典和字符串。像列表和字典在其他编程语言中可能称为数组，比如在PHP中，类似于列表格式的数组是最基本的，字典更像是关联数组，键唯一，且值可重复，最大的区别是，字典是无序的。所以无法通过索引去访问数据，但是php中的关联数组是有索引的，可以通过键去去访问，又可以通过索引去访问。

序列的索引可以是整数索引，也可以是负数索引，正数索引是从0开始，即下标为0表示第一个元素，下标为1表示第二个元素，·····以此类推

如果是负数索引，-1代表倒数第一个元素，-2代表倒数第二个元素，以此类推，如果序列中有n个元素，那-n就是第一元素，对应正数索引的下标为0的元素

除了可以使用索引来访问序列中的数据，还可以通过切片的方式来访问列表中的元素，他可以访问一定范围内的元素，使用切片操作还可以操作生成一个新的序列。语法如下：

sname[start: end: step]

• sname:序列的名称或者说是变量名

• start:切片开始的位置,如果不指定,则默认是0

• end:切片的截止位置,如果不指定,默认是序列的长度

• step:切片的步长,如果省略,默认为1,当省略该步长时,最后一个冒号也可以省略

序列的几种数据类型的用法基本类似,有关于序列的基本用法,这里就不再一一赘述,感兴趣的同学可以参考之前写过的相关文章:

《Python3 详细的数组基础操作 - 入门必备 [列表的操作]》

《五分钟拿捏 Python 字典 -Python3 入门必备 [字典详细操作]》

《Python 已有列表和字典, 为什么还需要元组?》

《唠唠 python 的作用域, 看看每个变量都为自己打下了多少江山》

接下来，咱们直接进入正题--利用Python实现斐波那契数列

斐波那契数列的实现流程

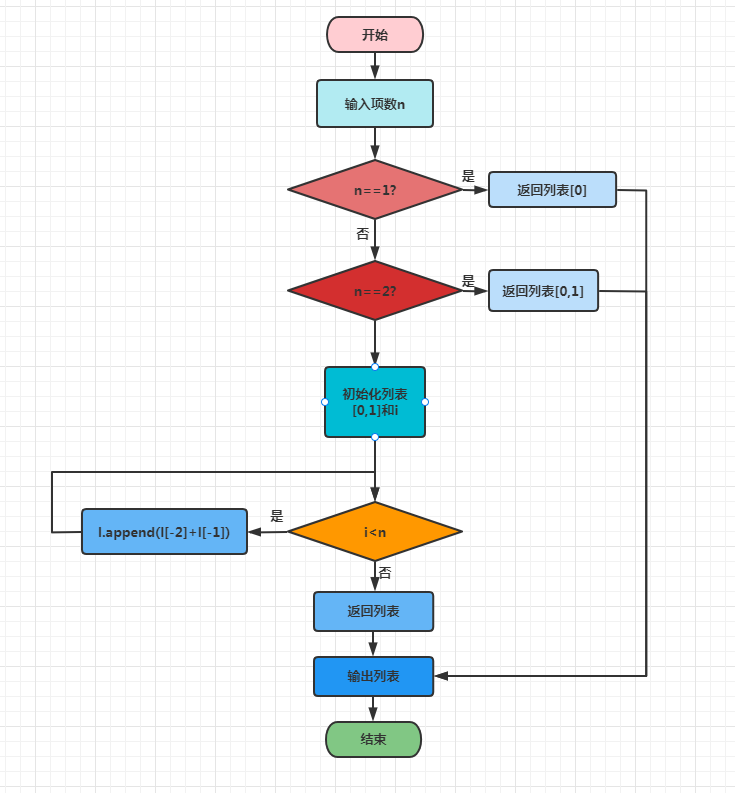
实现流程如下:

1. 输入要打印的斐波那契数列项数n

2. 判断需要输出的项数n是否等于1，若是，则返回列表[0],并输出返回列表,否则,则继续判断需要输出的项数n是否等于2,若是,则返回列表[0,1]并且输出返回的列表.否则初始化列表[0,1]和位置参数i

3. 判断i是否小于需要输出的项数n.若是,则执行l.append()方法,将列表中的最后一项和倒数第二项添加到列表中;否则返回列表

4. 输出返回的列表

5. 
   

代码实现:

定义fibo()函数,实现斐波那契数列的计算,并返回数列

def fibo(n):
    a = 0
    b = 1
    i = 0
    l = []
    while i < n :
        l.append(a)
        a,b = a+b,a
        i += 1
    return l

验证函数:

n = int(input("请输入斐波那契数列的项数:"))
print(fibo(n))

执行结果:

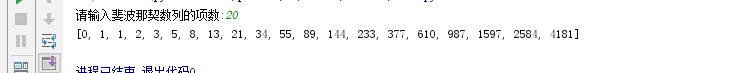
使用递归的方式实现斐波那契数列:

def fibo(n):
    if n<=1:
        return n
    else:
        return(fibo(n-1)+fibo(n-2))

n = int(input("请输入斐波那契数列的项数:"))

if n <=0:
    print("请输入大于0的整数！")
else:
    print("斐波那契数列：")
    l=[]
    for i in range(n):
        l.append(fibo(i))

    print(l)

执行结果如下: