✨力扣每日一题，797. 所有可能的路径！！！

✨题目

链接

给你一个有 n 个节点的 有向无环图（DAG） ，请你找出所有从节点 0 到节点 n-1 的路径并输出（不要求按特定顺序）

二维数组的第 i 个数组中的单元都表示有向图中 i 号节点所能到达的下一些节点，空就是没有下一个结点了。

译者注：有向图是有方向的，即规定了 a→b 你就不能从 b→a 。

示例 1：

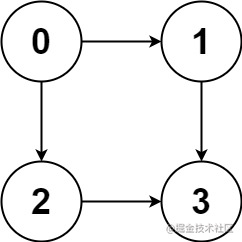
输入：graph = [[1,2],[3],[3],[]]

输出：[[0,1,3],[0,2,3]]

解释：有两条路径 0 -> 1 -> 3 和 0 -> 2 -> 3

示例 2：

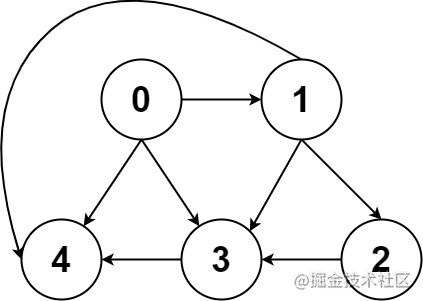
输入：graph = [[4,3,1],[3,2,4],[3],[4],[]]

输出：[[0,4],[0,3,4],[0,1,3,4],[0,1,2,3,4],[0,1,4]]

示例 3：

输入：graph = [[1],[]]
输出：[[0,1]]

示例 4：

输入：graph = [[1,2,3],[2],[3],[]]

输出：[[0,1,2,3],[0,2,3],[0,3]]

示例 5：

输入：graph = [[1,3],[2],[3],[]]

输出：[[0,1,2,3],[0,3]]

提示：

n == graph.length

2 <= n <= 15

0 <= graph[i][j] < n

graph[i][j] != i（即，不存在自环）

graph[i] 中的所有元素 互不相同

保证输入为 有向无环图（DAG）

🌈解题思路

其实这是比较经典的一个DFS题目

而且是有向图，也就是说可以按照他的路线走，不会重复，那么也不用去判断时候重复走过

😁案例讲解

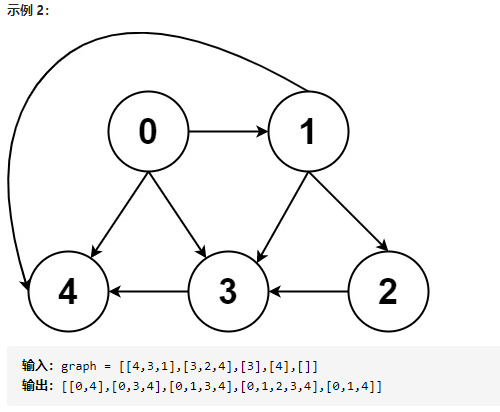
🔥以案例2为例

从0开始走，也就是起始点为索引0，索引为0的数组包含元素为：[4,3,1]

也就是说，从索引0可以到索引4或3或1，此时，list可以为0,4 或者 0,3或者0,1

以0,4为例，此时走到索引为4的数组，而索引为4的数组是空数组且是最后一个数组，那么0,4可作为一个答案

以0,3为例，此时走到索引为3的数组，而索引为3的数组为[4]，那么此时就应该是0,3,4了，在走到索引为4即最后一个数组，则0,3,4可做为一个答案

以0,1为例，此时走到索引为1的数组，而索引为1的数组为[3,2,4],那么此时，又有三条路线，即0,1,3,0,1,2,0,1,4，也就是又可以走到索引为3、2、4的位置

我就不继续往下推了，相信小伙伴看见上面的已经懂了！！！

🔥代码实现

class Solution {
    private List<List<Integer>> res = new ArrayList<>();

    public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
        dfs(0, graph, new ArrayList<Integer>());
        return res;
    }

    private void dfs(int index, int[][] graph, List<Integer> list){
        
        list.add(index);

        if (index == graph.length - 1) {         
            res.add(new ArrayList<>(list));
            return;
        }
        for (int i : graph[index]) {
            dfs(i, graph, list);
            list.remove(list.size() - 1);
        }
    }
}

💖最后

我是 Code皮皮虾，一个热爱分享知识的 皮皮虾爱好者，未来的日子里会不断更新出对大家有益的博文，期待大家的关注！！！

创作不易，如果这篇博文对各位有帮助，希望各位小伙伴可以==一键三连哦！==，感谢支持，我们下次再见~~~