软考中级(软件设计)——十进制转二进制的浮点数运算

​

原题：

把十进制数105.5转换成二进制数为___(2)__，转换成八进制数为____(3)___，转换成十六进制数为       (4)       。

解析文章：

二进制：软考中级(软件设计)——十进制转二进制的浮点数运算_红目香薰的博客-CSDN博客

八进制：软考中级(软件设计)——十进制转八进制的浮点数运算_红目香薰的博客-CSDN博客

十六进制：软考中级(软件设计)——十进制转十六进制的浮点数运算_红目香薰的博客-CSDN博客

二进制计算：1101001.1

前面的105，用二进制表示我们可以直接写出来：

105/2=52余1

52/2=26余0

26/2=13余0

13/2=6余1

6/2=3余0

3/2=1余1

1/2=0余1

余数自下而上拼接，故而有：

1101001这个二进制数是代表着105的十进制。

这里我们主要针对二进制浮点数进行说明：

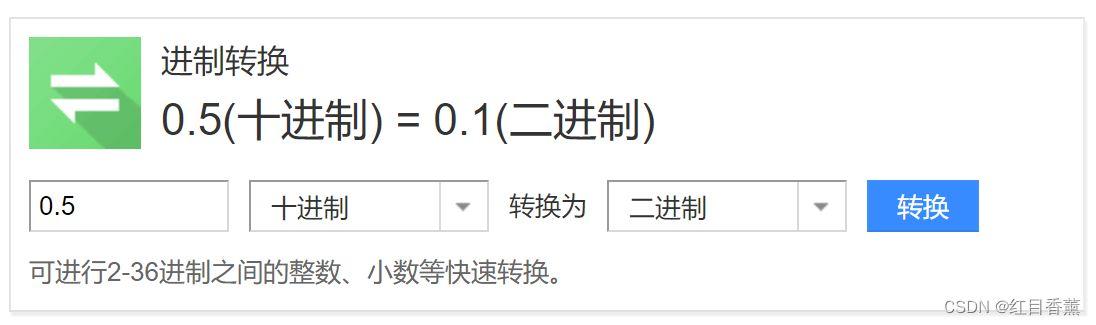
 浮点数的二进制我们需要单独理解一下，我们十进制是逢十进一，二进制是逢二进一，上图我是在百度上进行运算截取的图片，我在下文做了解释：

二进制中0.1+0.1=1。

二进制的1跟十进制的1是相等的，所以很明显二进制的0.1=十进制的1/2，也就是0.5。

这样就比较好理解了，所以我们105.5对应的二进制应该是：

1101001.1

拓展示例：

0.5是十进制数，因为小数点后面第1位对应十进制的基数（位权）是0.1，因此这位上的数5说明，有5个0.1。

二进制位权：个位=1，高位=低位*2，小数点后面也是如此，因此写出几位来看：

8 4 2 1. 1/2 1/4 1/8 也可以写成：8 4 2 1。0.5 0.25 0.125。

要表示0.5，只需要标记小数点后面第1位是1即可。

所以：0.5D=0.1B。

假设要表示0.625，那么0.625=0.5+0.125，因此表示成0.101B。

换句话说：0.101B表明，这个数包含1个0.5和1个0.125，需要对应位权来计数。

​