前言

在学习任何一个东西前，我们的必经之路依然是不落俗套地去了解它是什么。只有先了解他是什么，才知道他能做什么？之前的文章《【数据结构实践】手把手带你快速实现自定义二叉树》中我们详细介绍和实现了自定义二叉树，对二叉树有了基本的了解，那哈夫曼编码是什么呢，又能解决什么问题呢。接下来我们一起进入哈夫曼编码的探索之旅。

我们在计算机上看到的所有文字、图像、音频、视频等等,底层都是用二进制来存储和传输的。从狭义上来讲，把人类能看懂的各种信息，转换成计算机能够识别的二进制形式，被称为编码。编码的方式可以有很多种，比如:我们大家最熟悉的编码方式就属ASCII码了。在ASCII码当中，把每一个字符表示成特定的8位二进制数

何为哈夫曼编码？

哈夫曼编码(Huffman Coding)，又称霍夫曼编码，他是一种编码方式，哈夫曼编码是可变字长编码(VLC)的一种。Huffman于1952年提出一种编码方法，该方法完全依据字符出现概率来构造异字头的平均长度最短的码字，有时称之为最佳编码，一般就叫做Huffman编码(有时也称为霍夫曼编码)。

基本介绍：

在计算机数据处理中，哈夫曼编码使用变长编码表对源符号（如文件中的一个字母）进行编码，其中变长编码表是通过一种评估来源符号出现机率的方法得到的，出现机率高的字母使用较短的编码，否则出现机率低的则使用较长的编码，这便使编码之后的字符串的平均长度、期望值降低，从而达到无损压缩数据的目的。

例如：在英文中，e的出现机率最高，而z的出现概率则最低。当利用霍夫曼编码对一篇英文进行压缩时，e极有可能用一个比特来表示，而z则可能花去25个比特（不是26）。用普通的表示方法时，每个英文字母均占用一个字节（byte），即8个比特。二者相比，e使用了一般编码的1/8的长度，z则使用了3倍多。倘若我们能实现对于英文中各个字母出现概率的较准确的估算，就可以大幅度提高无损压缩的比例。

什么是哈夫曼树？

哈夫曼树【Huffman Tree】是指给定n个权值作为n个叶子节点，构造一棵二叉树，如果二叉树的带权路径长度达到最小,则这棵树被称为哈夫曼树

哈夫曼树又称最优二叉树，是一种带权路径长度最短的二叉树。所谓树的带权路径长度，就是树中所有的叶结点的权值乘上其到根结点的路径长度（若根结点为0层，叶结点到根结点的路径长度为叶结点的层数）。树的路径长度是从树根到每一结点的路径长度之和，记为WPL=（W1*L1+W2*L2+W3*L3+...+Wn*Ln），N个权值Wi（i=1,2,...n）构成一棵有N个叶结点的二叉树，相应的叶结点的路径长度为Li（i=1,2,...n）。可以证明霍夫曼树的WPL是最小的。

如何实现哈夫曼编码?

哈夫曼编码实现了两个重要目标：

1.任何一个字符编码，都不是其他字符编码的前缀。

2.信息编码的总长度最小。即所有叶子结点的（权重 X 路径长度）之和最小

过程演示

可利用二叉树进行二进制编码,具体流程如下:

比如现有一段信息里只有A，B，C，D，E这5个字符，他们出现的次数依次是3次，5次，9次，16次，20次，编码演示如下:

编码方式:

1.霍夫曼树的所有左链节点为0,右链节点为1

2.从树根至树叶依序记录所有字母的编码

步骤如下:

1.每个字母都代表一个终端节点（叶子节点），比较A，B，C，D，E五个字母中每个字母的出现频率，将最小的两个字母频率相加合成一个新的节点。发现A与B的频率最小，故3+5=8

2.比较8,C,D,E,其中8和C(9)的频率最小,所以8+9=17

⒊比较17,D,E,其中17和D(16)的频率最小,所以17+16=33

⒋剩下33,E,两者相加33+20=53

综上所述可得出下图:

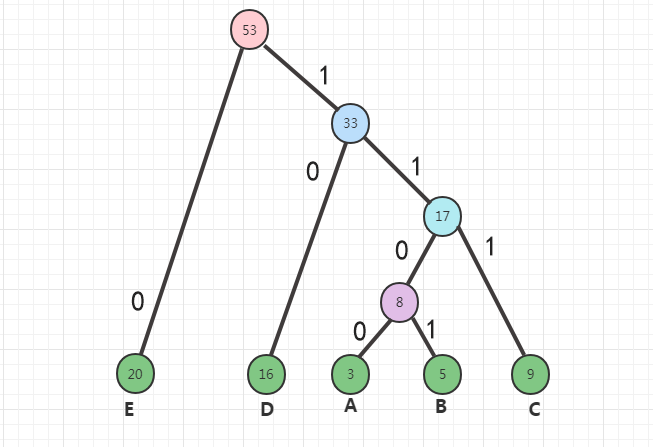
根据上图可得到如下数据:

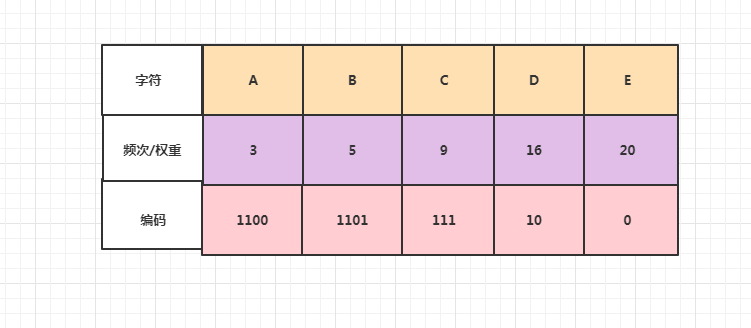
从上图可看出哈夫曼编码为可变字长编码.如果使用使用定长编码方式对以上字符进行编码,假如每个字符占3位,得到的总长度长度为:3*(3+5+9+16+20)=159

如果按照以上方式进行编码则得到的总长度为:4*3+4*5+3*9+2*16+1*20 = 111. 比定长编码短了30%左右

接下来进入实践阶段~~

代码实现

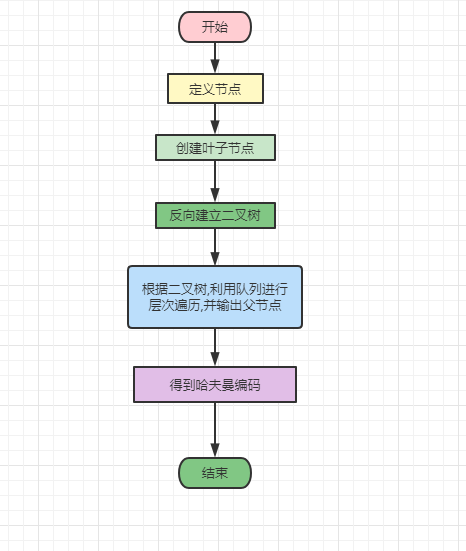
流程设计

1. 创建一个生成节点的函数.并将左右节点和父节点的初始值设置为None,从而定义节点

2. 创建叶子节点

3. 反向建立二叉树,并使用队列进行层次遍历各个节点,将各个节点的值作为数组,当该数组长度大于1时,构建新的哈夫曼树,最后返回队列

4. 将已建立的哈夫曼树的节点值输出的数组作为编码,通过循环最终得出哈夫曼编码

具体代码

定义创建节点的函数,并初始化

class generateNode:
    def __init__(self,frequency):
        self.left = None
        self.right = None
        self.father = None
        self.frequency = frequency
    def isLeft(self):
        return self.father.left == self

创建节点

def createNodes(frequency):
    return [generateNode(freq) for freq in frequency]

定义哈夫曼树函数,生成叶子节点,升序排序后,将最小值从队列中取出.赋值给左叶子节点,然后将次小值从队列中取出,赋值给右叶子节点,将两个值相加作为父节点,再将这个节点值放入队列中

def HuffmanTrees(nodes):
    queue = nodes[:]
    while len(queue) > 1:
        queue.sort(key=lambda item:item.frequency)
        node_left = queue.pop(0)
        node_right = queue.pop(0)
        node_father = generateNode(node_left.frequency + node_right.frequency)
        node_father.left = node_left
        node_left.father = node_father
        node_right.father = node_father
        queue.append(node_father)
    queue[0].father = None
    return queue[0]

定义输出哈夫曼编码函数.设定左子叶路径编码为0,右子叶路径编码为1

def getHuffmanEncodings(nodes,root):
    codes = [''] * len(nodes)
    for a in range(len(nodes)):
        node_tmp = nodes[a]
        while node_tmp != root:
            if node_tmp.isLeft():
                codes[a] = '0' + codes[a]
            else:
                codes[a] = '1' + codes[a]
            node_tmp = node_tmp.father
    return codes

验证结果

if __name__ == '__main__':
    chars_freqs = [('A', 3), ('B', 5), ('C', 9), ('D', 16), ('E', 20)]
    nodes = createNodes([item[1] for item in chars_freqs])
    root = HuffmanTrees(nodes)
    codes = getHuffmanEncodings(nodes,root)
    for item in zip(chars_freqs,codes):
        print ('字符:%s 出现频次:%-2d   编码: %s' % (item[0][0],item[0][1],item[1]))

执行结果如下:

总结

实现霍夫曼树的方式有很多种，可以使用优先队列简单达成这个过程，给与权重较低的符号较高的优先级。此算法的时间复杂度为O（n log n），因为有n个终端节点，所以树总共有2n-1个节点，使用优先队列每个循环须O（log n）。

此外，还有一个更快的方式使时间复杂度降至线性时间O(n)，即是使用两个队列（Queue）创建哈夫曼树。第一个队列用来存储n个符号（即n个终端节点）的权重，第二个队列用来存储两两权重的和（即非终端节点）。此法可保证第二个队列的前端（Front）权重永远都是最小值。虽然使用此方法比使用优先队列的时间复杂度还低，但是值得注意的是：此方法中节点必须依照权重大小加入队列中，如果节点加入顺序不按大小，则需要先经过排序，那么时间复杂度同样至少为O（n logn）

但是在不同的状况考量下，时间复杂度并非是最重要的，如我们本文中考虑英文字母的出现频率，变量n就是英文字母的26个字母，则使用哪一种算法时间复杂度都不会影响很大，因为n不是一笔庞大的数字。