前言

什么是堆

堆是一种数据结构，它是完全二叉树或者是近似完全二叉树的一种数据结构，树中每个结点的值都不小于(或不大于)其左右孩子结点的值。

何为完全二叉树

完全二叉树是一种特殊的二叉树，完全二叉树是除了最后一层之外的其他每一场层都被完全填充，叶子节点只能出现在最下层和次下层，并且最下面一层的结点都集中在该层最左边的若干位置的二叉树，也就是说所有节点都保持向左对齐。如果想了解更多关于二叉树的介绍，可参考之前写的一篇文章《【数据结构实践】手把手带你快速实现自定义二叉树》

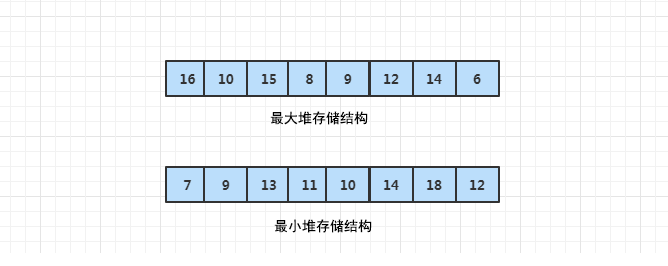
对完全二叉树来说，较为简洁的实现方法就是使用数组来存储完全二叉树。这样结点就按层序存储于数组中，其中第一个结点将存储于数组中的1号位，并且数组i号位表示的结点的左孩子就是2i号位，而右孩子则是(2i+1)号位。

什么是堆排序

堆排序与快速排序，归并排序一样都是时间复杂度为O(N*logN)的几种常见排序方法，堆排序是将数据看成完全二叉树，然后根据完全二叉树的特性来进行排序的一种排序算法，这有点草船借箭的妙用。正所谓他山之，石可以攻玉。在堆排序中，堆具体可分为最大堆和最小堆，也有人称他们为大顶堆和小顶堆，如果父节点的值大于或等于孩子结点的值，那么称这样的堆为最大堆，这时每个节点的值都是以其为根结点的子树的最大值，即最大堆要求节点的元素都大于其对应的叶子节点，通常被用来进行升序排序，如果父节点的值小于或等于孩子结点的值，那么称这样的堆为最小堆，这时每个节点的值都是以其为根结点的子树的最小值，即最小堆要求节点的元素都小于其对应的叶子节点，通常被用于降序排序。堆一般用于优先队列的实现，而优先队列默认情况下使用的是最大堆。

小结：

最大堆：每个节点的值都大于或者等于它的左右子节点的值。

最小堆：每个节点的值都小于或者等于它的左右子节点的值。

如下图：

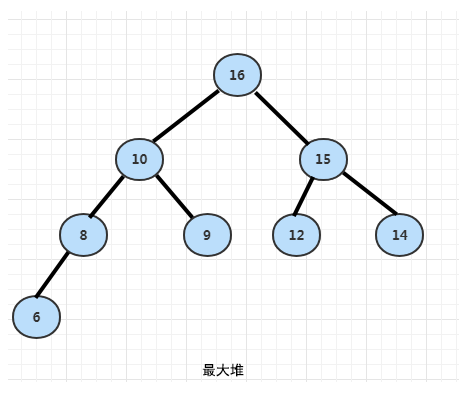
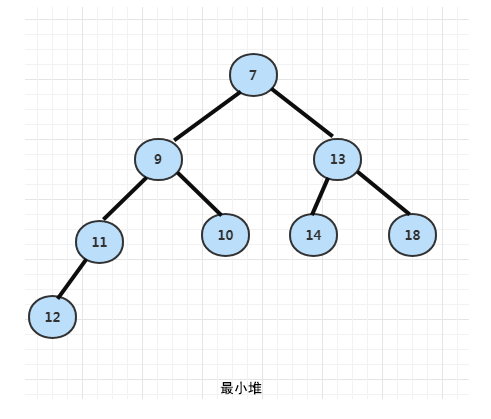
以最大堆为例，利用最大堆的结构特点，每个最大堆的根节点必然会是数组中最大的元素，构建一次最大堆，就可以获取数组中最大的元素。剔除最大元素后，反复构建剩下的数字为最大堆，获取根元素，最终保证数组有序。最大堆和最小堆是对称关系，学会其中一种即可

综上所述我们可以得出以下性质：

对于最大堆：arr[i] >= arr[2i + 1] && arr[i] >= arr[2i + 2]

对于最小堆：arr[i] <= arr[2i + 1] && arr[i] <= arr[2i + 2]

堆排序的算法设计

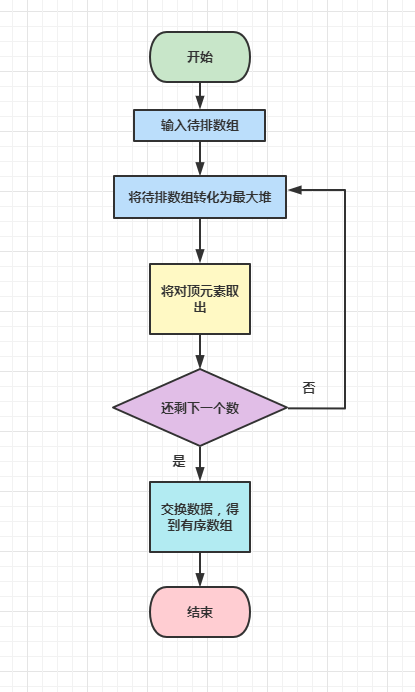
具体步骤如下：

1. 将待排序的数组构造成一个最大堆，根据最大堆的性质，当前堆的根节点（堆顶）就是序列中最大的元素

2. 数组转换成最大堆之后，将堆顶元素取出，然后将剩下的节点重新构建为最大堆

3. 重复步骤2，如此反复，直到剩余数只有一个时结束，从第一次构建大顶堆开始，每一次构建，我们都能获得一个序列的最大值

4. 交换数据，最后，就得到一个有序的数组了

代码实现

1.定义最大堆函数，传入当前节点的位置，左孩子位置是2*root+1.调整位置使堆顶元素最大

def siftdown(arr, node, end): #arr[i] >= arr[2i + 1] && arr[i] >= arr[2i + 2]
    root = node   # 当前节点的位置
    while True:
        # 从root开始对最大堆调整
        child = 2 * root +1  #左(left)孩子的位置
        if child  > end:
            break
        # 找出两个child中较大的一个
        if child + 1 <= end and arr[child] < arr[child + 1]: #如果左边小于右边
            child += 1 #左右两孩子中选择较大者
        if arr[root] < arr[child]:
            # 最大堆小于较大的child, 交换顺序
            tmp = arr[root]
            arr[root] = arr[child]
            arr[child]= tmp
            root = child #
        else:
            # 无需调整的时候, 跳出循环
            break

2.定义堆排序函数，传递待排数组，逐次遍历，

def heap_sort(arr):
    # 从最后一个有子节点的孩子开始调整最大堆，不断的缩小调整的范围直到第一个元素
    first = len(arr) // 2 -1
    for i in range(first, -1, -1):
        siftdown(arr, i, len(arr) - 1)
    # 将最大的放到堆的最后一个, 堆-1, 继续调整排序
    for end in range(len(arr) -1, 0, -1):
        arr[0], arr[end] = arr[end], arr[0]
        siftdown(arr, 0, end - 1)

验证堆排序算法：

def main():
    array = [16,10,15,8,9,12,14,6]
    print("原数组: ",array)
    heap_sort(array)
    print("排序后数组: ",array)
if __name__ == "__main__":
    main()

执行结果：

总结

一般需要排序的数据都存放于数组中，而堆排序使用了堆这个数据结构，相当于将堆嵌入到包含了序列的数组中，然后通过交换数组中的数据来进行排序，可以说是强行在数组中使用了堆结构。堆排序一开始需要将n个数据存进堆里，所需要时间为O（nlogn）。排序过程中，堆从空堆的状态开始，逐渐被数据填满，由于堆的高度小于log2n，所以插入1个数据所需要的时间是O（logn）。每轮取出最大的数据并重构堆需要的时间为O（logn），由于总共n轮，因此重构后排序的时间也是O（nlogn）。故整体看来堆排序的时间复杂度为O（nlogn），虽然堆排序整体运行效率不错，但是堆这个结构相对复杂，所以实现起来也较为困难。