【数据结构实践】手把手带你简单实现Python自定义栈

前言

何为栈?

栈又叫堆栈,它是一个有序集合.栈跟队列一样,也是一种呈线性排列的数据结构,而且两者极其相似,队列是先进先出(FIFO),而栈是后进先出(LILO).即像栈这种结构是最后添加的数据最先被取出,而且在这种结构中,我们只能访问最新添加的数据.栈就像一摞书,拿到新书时,我们就会把新书放在书堆上,取书的时候也只能从最上面的新书开始取.可看出它是是一种操作受限的线性表,所以往栈中添加和删除元素都是发生在同一端，通常称作发生操作的这一端为顶部，对应的端为底部.其实栈更像一个桶,你把东西放进桶里,你每次只能从最上面去拿,因为底下是封闭的,如果你想取下面的东西,就必须得先把上面的东西拿走.将目标物体暴露在最上面(栈顶)才行

栈有两种存储方式，即线性存储和链接存储（链表）。栈的一个最重要的特征就是栈的插入和删除只能在栈顶进行，所以每次删除的元素都是最后进栈的元素，故栈也被称为后进先出（LIFO）表。每个栈都有一个栈顶指针，它初始值为-1，且总是指向最后一个入栈的元素，栈有两种处理方式，即进栈（push）和出栈（pop），因为在进栈只需要移动一个变量存储空间，所以它的时间复杂度为O(1)，但是对于出栈分两种情况，栈未满时，时间复杂度也为O(1)，但是当栈满时，需要重新分配内存，并移动栈内所有数据，所以此时的时间复杂度为O(n)。以下举例栈结构的两种实现方式，线性存储和链接存储。

1.下图是线性存储的栈.这也是我们最常见的栈的存储方式,这也是本文的重点

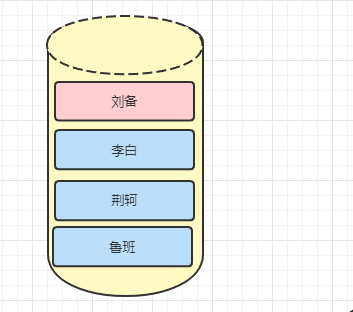
2.下图是是链链式存储的栈

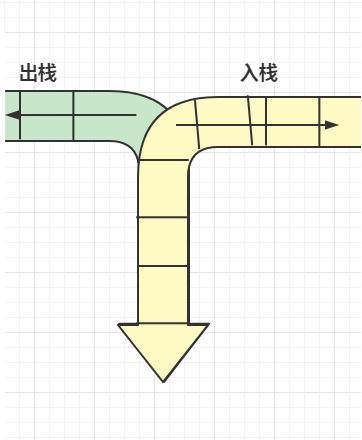
栈的操作演示

入栈操作

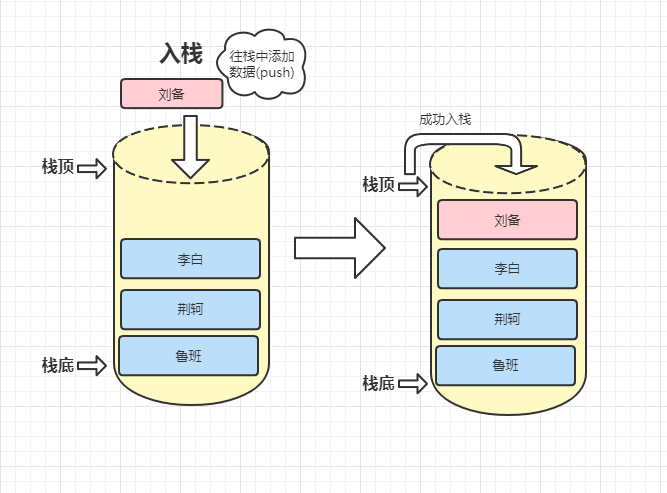
出栈操作

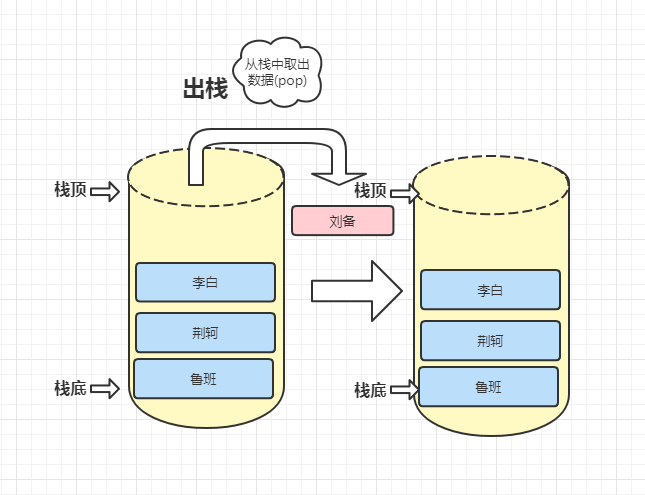
整个流程

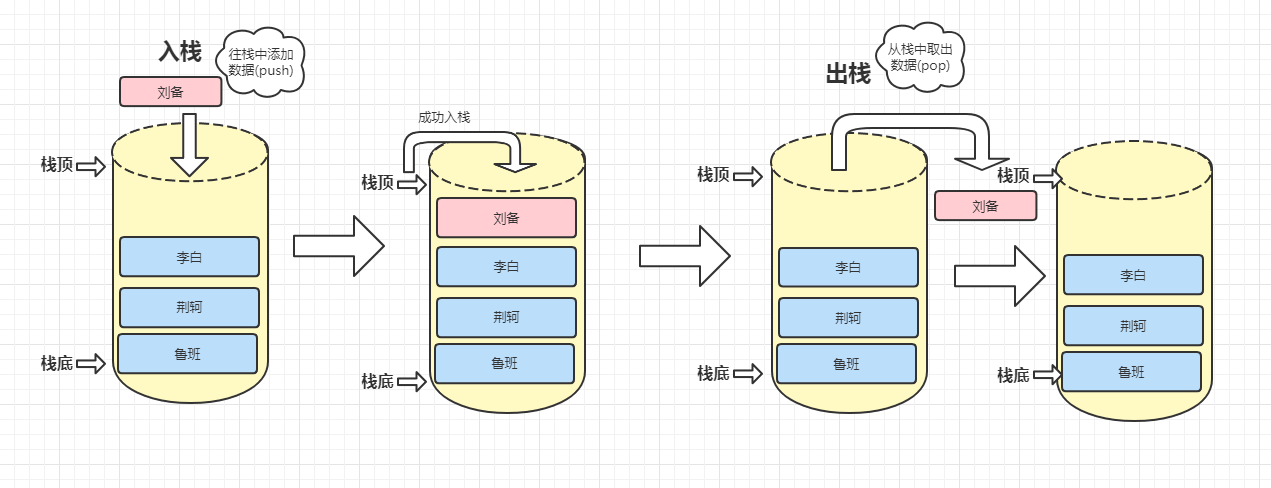
入栈:也叫压栈.就是向一个栈插入新元素.它是把新元素放到栈顶元素上面,使其成为新的栈顶元素

1. 若Top>=n,则给出溢出信息,作为出错处理(入栈前检查栈是否已满,满则溢出;就像桶装满水后,继续加水就会溢出,不满则入栈)

2. 设置Top=Top+1,栈指针加1.指向入栈地址

3. S(Top) =X,结束(X为新入栈的元素)

出栈:也加退栈,其实就是删除栈顶元素.是其相邻的元素成为栈顶元素

1. 若Top<=0,则给出溢出信息,作为出错处理(出栈前先检查栈是否已空,空则下溢,不空则出栈)

2. X=S(Top),出栈后的元素赋给X

3. Top=Top-1,结束.栈指针减1,指向栈顶

栈的设计流程

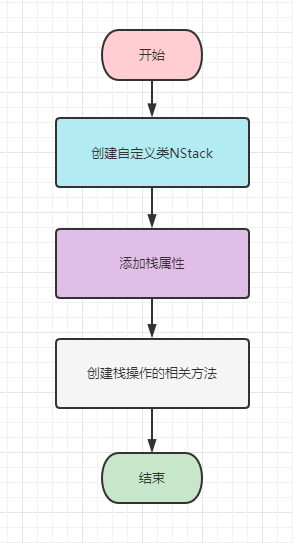
1. 创建自定义类NStack

2. 添加栈属性

3. 创建入栈,出栈,显示栈当前(栈顶)元素等方法

代码实现

1.创建NStack类,并设置其元素

class Stack:
    def __init__(self,size=5):
        self._content=[]
        self._size=size
        self._current=0

2.设置栈大小

    def setSize(self,size):  
       #如果缩小栈空间，则删除指定大小之后的已有元素  
        if size < self._current:  
            for i in range(size,self._current)[::-1]:  
                del self._current[i]  
            self._current = size  
        self._size = size 

3.实现出入栈相关操作方法

    def push(self,v):
        if self._current < self._size:
            self._content.append(v)  
            self._current = self._current + 1   #栈中元素个数加1 
        else:
            print('栈已满!')
    def pop(self):  
         if self._content:  
            self._current = self._current - 1 #栈中元素个数减1  
            return self._content.pop()  
         else:  
            print('栈为空!')

4.设置当前元素展示方法show()

    def show(self):  
        print(self._content)

5.其他方法:清空栈,判断栈是否已空或已满

    def isEmpty(self):  
        return not self._content  
    
    def isFull(self):  
        return self._current == self._size

6.验证NStack类:实例化并调用类的相关方法操作栈

s = NStack()
print('测试栈是否为空：',str(s.isEmpty()))
print('测试栈是否已满：',str(s.isFull()))
s.push(11)
s.push(21)
s.push('a')
print('添加元素后，显示栈当前元素：')
s.show()
s.setSize(3)
print('设置栈大小为3,并继续添加元素:')
s.push('b')
print('弹出元素:',str(s.pop()))

执行结果如下:

总结

栈只能在一端操作这一点看起来似乎非常不方便.但是在只需要访问最新数据时,使用栈就方便多了.比如,规定(A B ( C (D E) F ) (G ((H) I J) K))这一串字符中括号的处理方式如下:首先从左边开始读取字符,读到左括号就将其入栈,读到右括号就将栈顶的左括号出栈,此时,出栈的括号便与当前读取的右括号相匹配.通过这种处理方式,我们就能得知配对括号的具体位置