2023-05-14：你的赛车可以从位置 0 开始，并且速度为 +1 ，在一条无限长的数轴上行驶，

赛车也可以向负方向行驶，

赛车可以按照由加速指令 ‘A’ 和倒车指令 ‘R’ 组成的指令序列自动行驶。

当收到指令 ‘A’ 时，赛车这样行驶：

position += speed，

speed *= 2。

当收到指令 ‘R’ 时，赛车这样行驶：

如果速度为正数，那么speed = -1，

否则 speed = 1，

当前所处位置不变。

例如，在执行指令 “AAR” 后，赛车位置变化为 0 --> 1 --> 3 --> 3，

速度变化为 1 --> 2 --> 4 --> -1，

给你一个目标位置 target ，返回能到达目标位置的最短指令序列的长度。

输入：target = 3。

输出：2。

答案2023-05-14：

算法1 - Dijkstra 算法

1.初始化

1.1.设置变量 maxp，表示当前速度下能达到的最大位置，同时计算最大速度 maxs；

1.2.初始化一个优先队列（堆），保存状态 state{speed, cost, position}，其中 speed 表示当前速度，cost 表示到达该状态所需的步数，position 表示当前位置；

1.3.根据最初的位置和速度创建初始状态，将其压入优先队列中。

2.Dijkstra 算法遍历状态空间

2.1.从优先队列中取出当前代价最小/速度绝对值最大的状态 state0；

2.2.若该状态满足目标条件，则返回其代价 cost；

2.3.否则，考虑在该状态基础上执行 A 或 R 操作后能够到达的状态：

2.3.1.若执行 A 操作，则新状态为 {speed+1, cost+1, position+(1<<(speed-1))}，必须满足新位置不超过 maxp、未访问过；

2.3.2.若执行 R 操作，则新状态为 {speed>0?-1:1, cost+1, position}，无需判断是否超过边界、未访问。

2.4.将所有可行的新状态加入优先队列，并继续进行 Dijkstra 遍历。

3.返回 -1，如果无法到达目标位置。

时间复杂度：O(T log T)，其中 T 是目标位置 target。每个状态最多被扩展一次，因此总共扩展的状态数不会超过 O(T)。在优先队列中插入和弹出元素的时间复杂度为 O(log T)，因此总时间复杂度为 O(T log T)。

空间复杂度：O(T log T)。需要开辟一个大小为 O(T log T) 的优先队列、两个大小为 O(T log T) 的二维数组 visitedPositive 和 visitedNegative，以及一个大小为 O(T) 的判断是否访问过的数组。

算法2 - 动态规划

1.初始化

1.1.创建长度为 target+1 的数组 dp，用于保存到达每个位置的最短步数；

1.2.调用 process(target, dp) 函数进行递归求解。

2.递归求解

2.1.若 dp[target] > 0，说明已经计算过到达该位置的最短步数，直接返回 dp[target]；

2.2.计算当前速度下能够到达的最远位置 maxp 和最大速度 maxs；

2.3.如果目标位置就在当前速度达不到的位置之前，则必须先倒车，再加速到目标位置；

若目标位置恰好与当前速度所达到的最远位置相同，则无需倒车。

2.4.对于以上情况，分别计算：

2.4.1.倒车后可以到达的位置 beyond = speed-1-target；

2.4.2.从新的位置开始加速到目标位置，需要的最短步数为 process(beyond, dp)，

在此基础上需要增加 1 次倒车操作和 1 次加速操作，因此总步数为 steps+1+process(beyond, dp)。

2.5.如果目标位置在当前速度达到的范围内，则直接加速即可。计算需要的最短步数，以及在此基础上还需要多少次加速操作（steps），

然后遍历所有加速操作的次数 back，计算倒车后可以到达的位置 lack 和需要的步数 steps+1+back+1+process(lack, dp)，

取其中的最小值即为当前情况下的最短步数。

2.6.将结果保存到数组 dp 中，并返回。

3.返回 dp[target]。

时间复杂度：O(T log T)。虽然是递归求解，但是可以使用记忆化优化，避免重复计算。每个位置最多只会被计算一次，因此总时间复杂度为 O(T)。

空间复杂度：O(T)。需要创建一个大小为 O(T) 的数组 dp 保存中间结果。

go完整代码如下：

package main

import (
	"container/heap"
	"fmt"
)

type state struct {
	speed, cost, position int
}

type priorityQueue []state

func (pq priorityQueue) Len() int { return len(pq) }
func (pq priorityQueue) Less(i, j int) bool {
	return pq[i].cost > pq[j].cost
}
func (pq priorityQueue) Swap(i, j int) { pq[i], pq[j] = pq[j], pq[i] }

func (pq *priorityQueue) Push(x interface{}) {
	item := x.(state)
	*pq = append(*pq, item)
}

func (pq *priorityQueue) Pop() interface{} {
	old := *pq
	n := len(old)
	item := old[n-1]
	*pq = old[0 : n-1]
	return item
}

func abs(x int) int {
	if x < 0 {
		return -x
	}
	return x
}

func racecar1(target int) int {
	maxp := 0
	maxs := 1
	for maxp <= target {
		maxp += 1 << (maxs - 1)
		maxs += 1
	}

	heap0 := &priorityQueue{}
	visitedPositive := make([][]bool, maxs+1)
	visitedNegative := make([][]bool, maxs+1)
	for i := range visitedPositive {
		visitedPositive[i] = make([]bool, maxp+1)
		visitedNegative[i] = make([]bool, maxp+1)
	}

	heap.Push(heap0, state{
		speed:    1,
		cost:     0,
		position: 0,
	})

	for heap0.Len() > 0 {
		current := heap.Pop(heap0).(state)
		speed := current.speed
		cost := current.cost
		position := current.position
		if position == target {
			return cost
		}
		if speed > 0 {
			if visitedPositive[speed][position] {
				continue
			}
			visitedPositive[speed][position] = true
			add(
				speed+1,
				cost+1,
				position+(1<<(speed-1)),
				maxp,
				heap0,
				visitedPositive,
			)
			add(
				-1,
				cost+1,
				position,
				maxp,
				heap0,
				visitedNegative,
			)
		} else {
			speed := -speed
			if visitedNegative[speed][position] {
				continue
			}
			visitedNegative[speed][position] = true
			add(
				-(speed + 1),
				cost+1,
				position-(1<<(speed-1)),
				maxp,
				heap0,
				visitedNegative,
			)
			add(
				1,
				cost+1,
				position,
				maxp,
				heap0,
				visitedPositive,
			)
		}
	}
	return -1
}

func add(
	speed int,
	cost int,
	position int,
	limit int,
	heap0 *priorityQueue,
	visited [][]bool,
) {
	if position >= 0 && position <= limit && !visited[abs(speed)][position] {
		heap.Push(heap0, state{
			cost:     cost,
			speed:    speed,
			position: position,
		})
	}
}

// 动态规划 + 数学
func racecar2(target int) int {
	dp := make([]int, target+1)
	return process(target, dp)
}

func process(target int, dp []int) int {
	if dp[target] > 0 {
		return dp[target]
	}
	steps := 0
	speed := 1
	for speed <= target {
		speed <<= 1
		steps++
	}
	ans := 0
	beyond := speed - 1 - target
	if beyond == 0 {
		ans = steps
	} else {
		ans = steps + 1 + process(beyond, dp)
		steps--
		speed >>= 1
		lack := target - (speed - 1)
		offset := 1
		for back := 0; back < steps; back++ {
			ans = min(ans, steps+1+back+1+process(lack, dp))
			lack += offset
			offset <<= 1
		}
	}
	dp[target] = ans
	return ans
}

func min(a, b int) int {
	if a < b {
		return a
	}
	return b
}

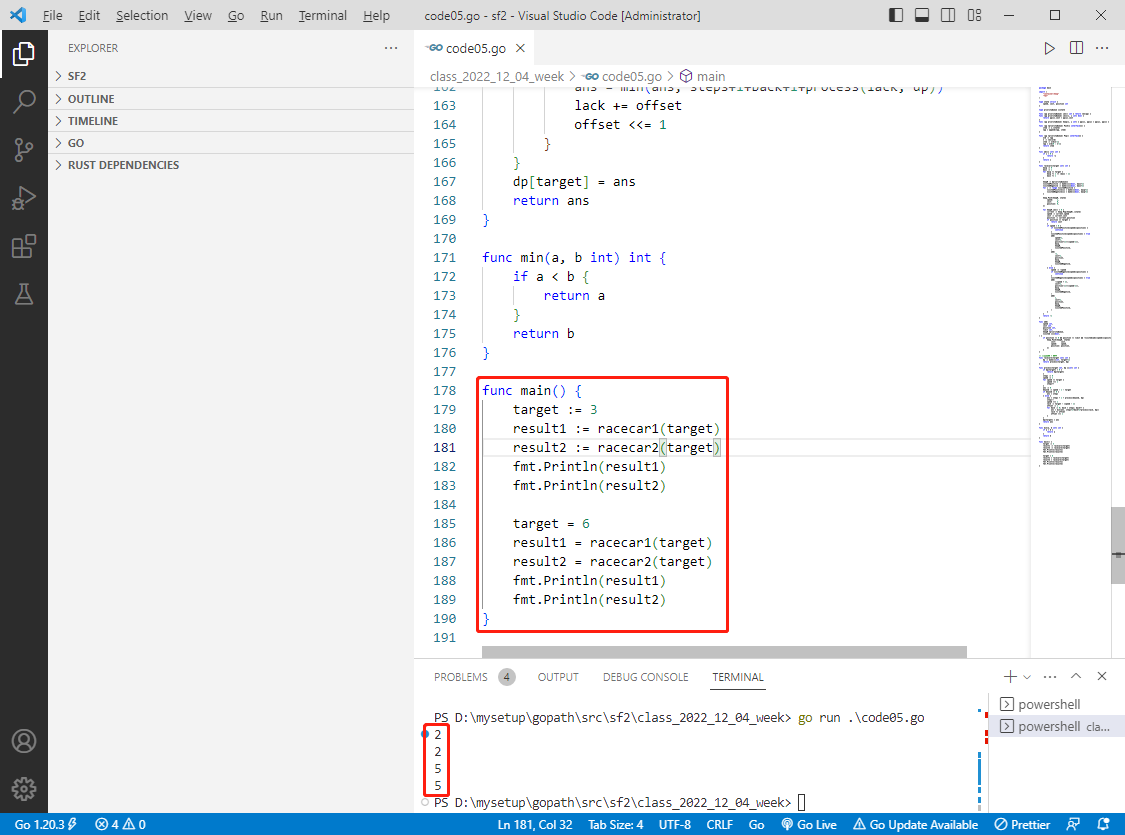
func main() {
	target := 3
	result1 := racecar1(target)
	result2 := racecar2(target)
	fmt.Println(result1)
	fmt.Println(result2)

	target = 6
	result1 = racecar1(target)
	result2 = racecar2(target)
	fmt.Println(result1)
	fmt.Println(result2)
}

rust完整代码如下：

use std::cmp::Reverse;
use std::collections::BinaryHeap;

fn racecar1(target: i32) -> i32 {
    let mut maxp = 0;
    let mut maxs = 1;
    while maxp <= target {
        maxp += 1 << (maxs - 1);
        maxs += 1;
    }
    // 0 : 几倍速
    // 1 : 花费了几步
    // 2 : 当前位置
    let mut heap = BinaryHeap::new();
    let mut positive = vec![vec![false; (maxp + 1) as usize]; (maxs + 1) as usize];
    let mut negative = vec![vec![false; (maxp + 1) as usize]; (maxs + 1) as usize];
    heap.push((Reverse(0), Reverse(1), Reverse(0)));
    while let Some((Reverse(cost), Reverse(speed), Reverse(position))) = heap.pop() {
        if position == target {
            return cost;
        }
        if speed > 0 {
            if positive[speed as usize][position as usize] {
                continue;
            }
            positive[speed as usize][position as usize] = true;
            add(
                speed + 1,
                cost + 1,
                position + (1 << (speed - 1)),
                maxp,
                &mut heap,
                &positive,
            );
            add(-1, cost + 1, position, maxp, &mut heap, &negative);
        } else {
            let speed = -speed;
            if negative[speed as usize][position as usize] {
                continue;
            }
            negative[speed as usize][position as usize] = true;
            add(
                -(speed + 1),
                cost + 1,
                position - (1 << (speed - 1)),
                maxp,
                &mut heap,
                &negative,
            );
            add(1, cost + 1, position, maxp, &mut heap, &positive);
        }
    }
    -1
}

fn add(
    speed: i32,
    cost: i32,
    position: i32,
    limit: i32,
    heap: &mut BinaryHeap<(Reverse<i32>, Reverse<i32>, Reverse<i32>)>,
    visited: &Vec<Vec<bool>>,
) {
    if position >= 0 && position <= limit && !visited[speed.abs() as usize][position as usize] {
        heap.push((Reverse(cost), Reverse(speed), Reverse(position)));
    }
}

fn racecar2(target: i32) -> i32 {
    let mut dp = vec![0; (target + 1) as usize];
    process(target, &mut dp)
}

fn process(target: i32, dp: &mut Vec<i32>) -> i32 {
    if dp[target as usize] > 0 {
        return dp[target as usize];
    }
    let mut steps = 0;
    let mut speed = 1;
    while speed <= target {
        speed <<= 1;
        steps += 1;
    }
    let mut ans = 0;
    let beyond = speed - 1 - target;
    if beyond == 0 {
        ans = steps;
    } else {
        ans = steps + 1 + process(beyond, dp);
        steps -= 1;
        speed >>= 1;
        let mut lack = target - (speed - 1);
        let mut offset = 1;
        for back in 0..steps {
            ans = ans.min(steps + 1 + back + 1 + process(lack, dp));
            lack += offset;
            offset <<= 1;
        }
    }
    dp[target as usize] = ans;
    ans
}

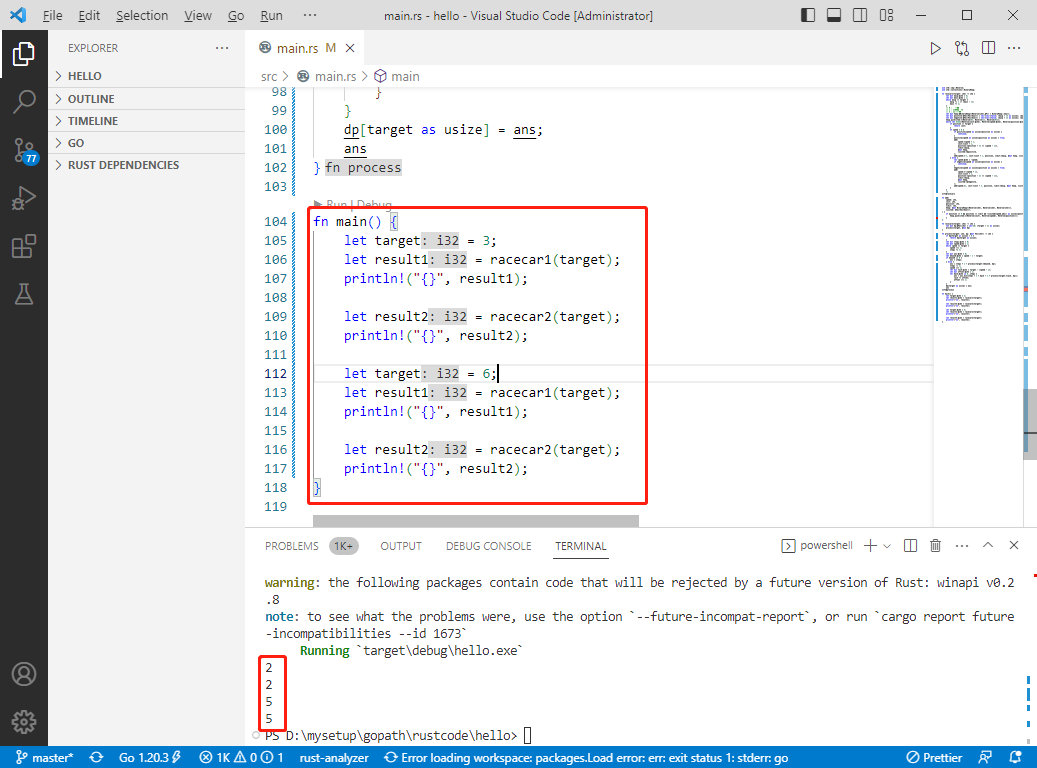
fn main() {
    let target = 3;
    let result1 = racecar1(target);
    println!("{}", result1);

    let result2 = racecar2(target);
    println!("{}", result2);

    let target = 6;
    let result1 = racecar1(target);
    println!("{}", result1);

    let result2 = racecar2(target);
    println!("{}", result2);
}

c语言第二种方法代码如下：

#include <stdio.h>
#include <stdlib.h>

int racecar2_helper(int target, int* dp) {
    if (dp[target] > 0) {
        return dp[target];
    }
    int steps = 0;
    int speed = 1;
    while (speed <= target) {
        speed <<= 1;
        steps++;
    }
    int ans = 0;
    int beyond = speed - 1 - target;
    if (beyond == 0) {
        ans = steps;
    }
    else {
        ans = steps + 1 + racecar2_helper(beyond, dp);
        steps--;
        speed >>= 1;
        int lack = target - (speed - 1);
        int offset = 1;
        for (int back = 0; back < steps; back++) {
            ans = (ans < steps + 1 + back + 1 + racecar2_helper(lack, dp)) ?
                ans : steps + 1 + back + 1 + racecar2_helper(lack, dp);
            lack += offset;
            offset <<= 1;
        }
    }
    dp[target] = ans;
    return ans;
}

int racecar2(int target) {
    int* dp = (int*)calloc((target + 1), sizeof(int));
    int result = racecar2_helper(target, dp);
    free(dp);
    return result;
}

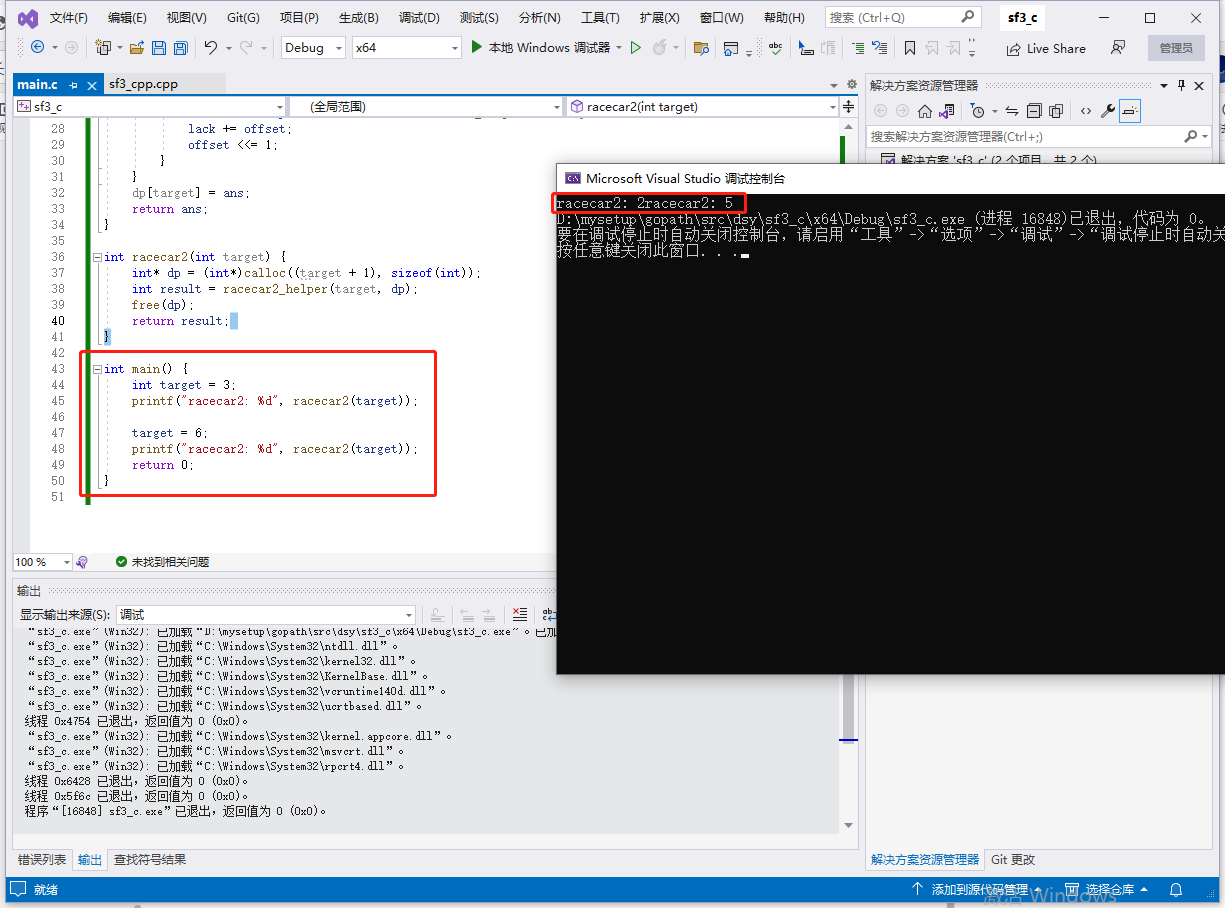
int main() {
    int target = 3;
    printf("racecar2: %d", racecar2(target));
    target = 6;
    printf("racecar2: %d", racecar2(target));
    return 0;
}

c++第二种方法代码如下：

#include <iostream>
#include <vector>

using namespace std;

int racecar2_helper(int target, vector<int>& dp) {
    if (dp[target] > 0) {
        return dp[target];
    }
    int steps = 0;
    int speed = 1;
    while (speed <= target) {
        speed <<= 1;
        steps++;
    }
    int ans = 0;
    int beyond = speed - 1 - target;
    if (beyond == 0) {
        ans = steps;
    }
    else {
        ans = steps + 1 + racecar2_helper(beyond, dp);
        steps--;
        speed >>= 1;
        int lack = target - (speed - 1);
        int offset = 1;
        for (int back = 0; back < steps; back++) {
            ans = min(ans, steps + 1 + back + 1 + racecar2_helper(lack, dp));
            lack += offset;
            offset <<= 1;
        }
    }
    dp[target] = ans;
    return ans;
}

int racecar2(int target) {
    vector<int> dp(target + 1, 0);
    return racecar2_helper(target, dp);
}

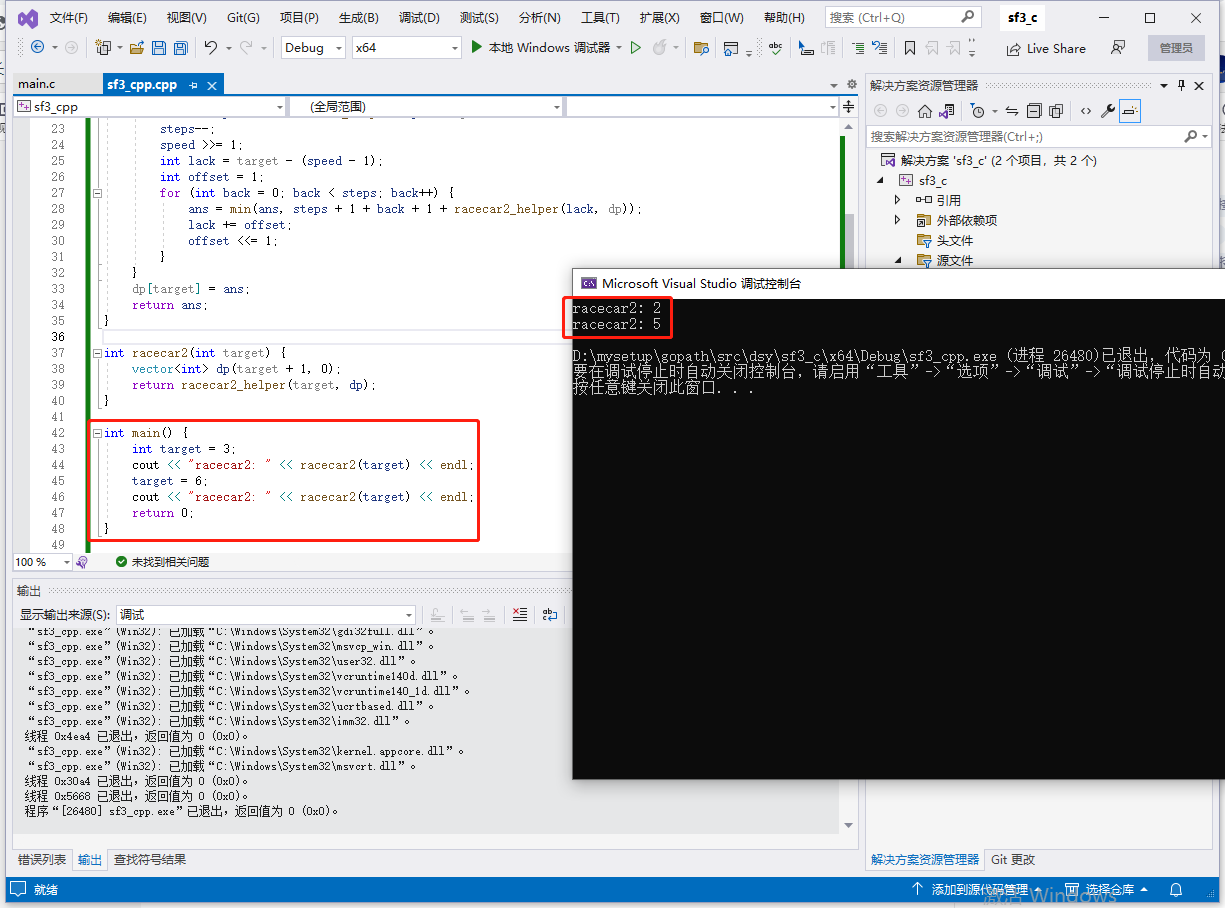
int main() {
    int target = 3;
    cout << "racecar2: " << racecar2(target) << endl;
    target = 6;
    cout << "racecar2: " << racecar2(target) << endl;
    return 0;
}