【数据结构实践】从0到1带你利用Python实现自定义集合

前言

集合(简称集)是数学中一个基本概念,我们应该都比较熟悉,不管是生活中,还是数学上,我们都频繁地接触到。集合在数学领域具有无可比拟的特殊重要性。一定范围的，确定的，可以区别的事物，当作一个整体来看待，就叫做集合，简称集，其中各事物叫做集合的元素或简称元。如(1)阿Q正传中出现的不同汉字(2)全体英文大写字母。任何集合是它自身的子集。它是集合论的研究对象，集合论的基本理论直到19世纪才被创立。集合论的基础是由德国数学家康托尔在19世纪70年代奠定的，经过一大批卓越的科学家半个世纪的努力，到20世纪20年代已确立了其在现代数学理论体系中的基础地位，可以说，现代数学各个分支的几乎所有成果都构筑在严格的集合理论上。集合具有确定性、互异性、无序性、纯粹性和完备性等性质

最简单的说法，即是在最原始的集合论--朴素集合论中的定义，集合就是"一堆东西"。集合里的"东西"，叫作元素。若x是集合A的元素，则记作x∈A。集合是把人们的直观的或思维中的某些确定的能够区分的对象汇合在一起，使之成为一个整体(或称为单体)，这一整体就是集合。组成一集合的那些对象称为这一集合的元素(或简称为元)。现代数学还用"公理"来规定集合。

不但在数学上能够频繁接触到集合的知识，学习过java的童鞋应该非常熟悉这一概念,java的集合类型中有List，Set，Map。List是有序可重复的；Set是无序，不可重复的；Map是键值对，键值唯一，值可重复。可以看出Set更符合我们今天所说的数学上的集合。在数学上，把由不同元素组成的容器叫做集合，而Python引入了这一概念，集合对象是一组无序的可哈希的值，在Python中集合有两种不同的类型，即可变集合和不可变集合，可变集合可以像列表一样删除和添加元素，对于不可变集合来说，则不允许这样做。本文将从集合的定义和常见的操作来展开介绍

集合的定义

集合的定义主要有以下几点：

• 集合是无序的，所以不支持用下标索引来查找元素。

• 集合中的每一个元素都是唯一的

• 集合是一种可变的数据类型

集合的常见操作

最常见的操作就是添加元素和删除元素：

1.向集合中添加元素

1. add():将添加的元素作为一个整体处理.

2. update():将添加的元素拆分,作为个体传入集合中.

2.删除集合的元素

1. remove():删除集合中的具体的值,如果集合中没有这个值,则程序报错.

2. pop():随机删除集合中的某个元素,如果集合为空,则程序报错.

3. discard():如果元素存在,直接删除,如果元素不存在,程序不会报错,不做任何操作

4. clear():集合清空,集合为空

集合的运算

集合的运算主要有交集、并集和差集：

• 1) 交集:含有既属于A又属于B的元素，没有其他元素的集合。使用操作符“&”执行交集操作，也可使用intersection( )方法完成。

• 2) 并集:包含一组集合的所有元素，而不包含其他元素构成的集合。使用操作符“|”执行并集操作，同样也可使用union( )方法完成。

• 3) 差集:所有属于A且不属于B的元素构成的集合。使用操作符“一”执行差集操作，同样也可使用difference( )方法完成。

主体设计

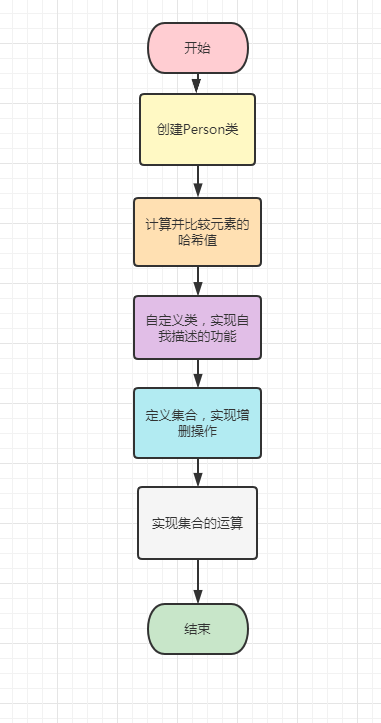
使用Python自定义可变集合，实现创建集合、添加或删除元素，以及求交集、并集、差集等一系列运算，步骤如下：

1. 创建自定义Person类。

2. 使用_ hash_ 哈希算法， 把形参转为-一个数值， 再用_ eq _把转换过来的数值进行比较。

3. 使用_ repr_ 自定 义类，实现自我描述的功能。

4. 定义两个集合，实现添加、删除数据。

5. 实现集合的运算并输出。

编程实现

创建Person类

class Person:
    def __init__(self, name, idCard):
        self.name = name
        self.idCard = idCard

    #使用__hash__算法,把形参转为一个hash值,然后使用__eq__把转换过来的哈希值进行比较
    def __hash__(self):
        return  self.name.__hash__()

    def __eq__(self, other):
        if self.idCard == other.idCard:
            return True
        return False
      
    #定义集合格式
    def __repr__(self):
        return self.name + ':' + self.idCard

调用Person自定义集合

p1 = Person('zs','1231')
p2 = Person('李四','1231')
p3 = Person('zs','1232')
p4 = Person('王五','1233')
p5 = Person('赵六','1233')
p6 = Person('赵六','1234')
p7 = Person('赵六','1234')

x1 = {p1,p2,p3,p4,p5,p6,p7}
myset = set(x1)
print("集合x为:", myset)

输出结果:

集合x为: {王五:1233, zs:1231, 赵六:1233, 赵六:1234, zs:1232, 李四:1231}

当name和idCard相同时,表示同一个元素,因为集合是唯一的只会保留一个

对集合进行增删操作

其实增删操作还可以自定义,这里使用的set自带的方法

p8 = Person('鲁班','1237')
p9 = Person('韩信','1238')
myset.add(p8)
myset.add(p9)

print('新增元素之后的集合为:', myset)

新增执行结果:

原集合为: {zs:1231, zs:1232, 王五:1233, 赵六:1233, 李四:1231, 赵六:1234}
新增元素之后的集合为: {韩信:1238, zs:1231, zs:1232, 王五:1233, 赵六:1233, 李四:1231, 鲁班:1237, 赵六:1234}

删除操作代码如下:

myset.remove(p4)

print('删除p4元素之后的集合为:', myset)

执行结果如下:这里会把'王五:1233'对应的元素删除

删除p4元素之后的集合为: {zs:1231, zs:1232, 鲁班:1237, 韩信:1238, 李四:1231, 赵六:1234, 赵六:1233}

集合的运算实现

接着上面的代码进行操作

新建集合2

# 新建一个集合
x2 = {p8,p9,p10,p11}
set2 = set(x2)
print('集合2为:', set2)

执行结果:集合1是删除元素之前的集合

集合1为: {李四:1231, 王五:1233, zs:1231, 鲁班:1237, 赵六:1233, 韩信:1238, zs:1232, 赵六:1234}
集合2为: {李白:1544, 刘备:1534, 鲁班:1237, 韩信:1238}

集合运算:

并集

print('集合1和集合2的并集为:', myset | set2)

执行结果:

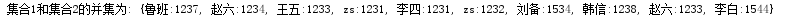
交集

print('集合1和集合2的交集为:', myset & set2)

执行结果:

集合1和集合2的交集为: {鲁班:1237, 韩信:1238}

差集

print('集合1和集合2的差集为:', myset - set2)

执行结果:

集合1和集合2的差集为: {赵六:1234, 王五:1233, zs:1231, 李四:1231, zs:1232, 赵六:1233}

集合的运算就跟四则运算一样简单.