AI人工智能逻辑回归的原理、优缺点、应用场景和实现方法

逻辑回归（Logistic Regression）是一种常见的机器学习算法，它被广泛应用于分类问题。在人工智能（Artificial Intelligence，简称AI）领域中，逻辑回归是一种简单而有效的算法，可以用于许多应用领域，如医疗、金融、电商等。本文将详细介绍AI人工智能逻辑回归的原理、优缺点、应用场景和实现方法。

原理

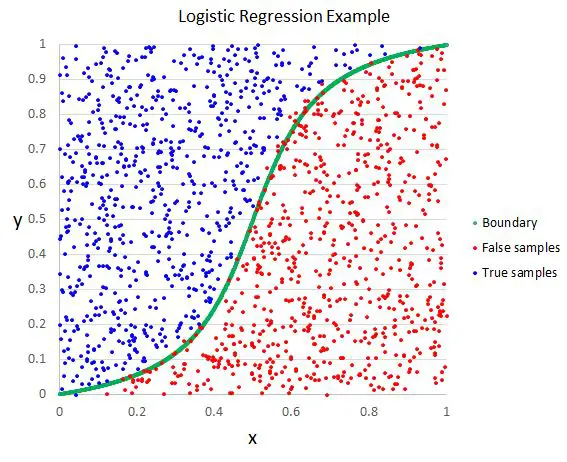
逻辑回归是一种针对二分类问题的线性模型，它可以将输入特征映射到输出类别的概率。逻辑回归的核心思想是使用sigmoid函数将线性回归的输出转化为概率值，然后根据阈值将概率值转化为类别标签。

假设有一个二分类问题，输入特征为 $x\in R^n$，输出类别为 $y\in\{0,1\}$，逻辑回归的模型可以表示为：

$$h(x)=\frac{1}{1+e^{-w^Tx}}$$

其中 $w\in R^n$是模型的权重参数， $h(x)$表示输出类别为1的概率值。sigmoid函数可以将线性回归的输出转化为0到1之间的概率值，其公式为：

$$sigmoid(z)=\frac{1}{1+e^{-z}}$$

其中 $z=w^Tx$是线性回归的输出。当 $h(x)\geq0.5$时，预测类别为1，否则预测类别为0。

逻辑回归的模型参数可以通过最大似然估计或梯度下降等方法来学习。最大似然估计是一种常用的参数估计方法，其目标是最大化训练数据的似然函数，使得模型能够更好地拟合训练数据。梯度下降是一种常用的优化算法，其目标是最小化损失函数，使得模型能够更好地泛化到未见过的数据。

优缺点

逻辑回归作为一种简单而有效的分类算法，具有以下优缺点：

优点：

1. 简单易懂：逻辑回归是一种基于线性模型的算法，易于理解和实现。

2. 计算效率高：逻辑回归的计算复杂度较低，可以快速处理大规模数据集。

3. 可解释性强：逻辑回归可以通过系数来解释变量对分类结果的影响。

4. 鲁棒性强：逻辑回归对异常数据的影响较小，具有较好的鲁棒性。

缺点：

1. 仅适用于线性分类问题：逻辑回归只适用于线性可分的二分类问题，对于非线性分类问题无法处理。

2. 容易受到噪声干扰：逻辑回归对噪声数据比较敏感，容易受到干扰。

3. 不适用于多分类问题：逻辑回归只适用于二分类问题，无法直接处理多分类问题。

应用场景

逻辑回归在人工智能领域中有广泛的应用，常见的应用场景包括以下几种：

1. 信用评估：逻辑回归可以用于信用评估，根据用户的信用信息预测其是否会违约。

2. 医疗诊断：逻辑回归可以用于医疗诊断，根据患者的临床数据预测其是否患有某种疾病。

3. 电商推荐：逻辑回归可以用于电商推荐，根据用户的购买历史和浏览行为预测其是否会购买某种商品。

4. 舆情分析：逻辑回归可以用于舆情分析，根据新闻和社交媒体的内容预测其情感倾向。

实现方法

在实现逻辑回归模型时，通常需要进行以下几个步骤：

1. 数据预处理：包括数据清洗、特征选择、特征缩放等处理过程，以提高模型的准确性和稳定性。

2. 模型训练：包括模型的初始化、参数估计、损失函数的最小化等训练过程，以学习模型的参数。

3. 模型评估：包括模型的准确率、精度、召回率等指标的计算，以评估模型的性能。

4. 模型应用：包括利用模型进行预测、推荐、分类等任务，以应用于实际问题中。

在实现逻辑回归模型时，可以使用现有的机器学习库，如scikit-learn、TensorFlow等，也可以自己编写代码实现。使用现有的机器学习库可以大大简化模型的实现过程，提高开发效率和代码质量。自己编写代码可以更好地理解逻辑回归的原理和实现方法，以便在实际问题中进行调整和优化。

总结

本文介绍了AI人工智能逻辑回归的原理、优缺点、应用场景和实现方法。逻辑回归作为一种简单而有效的分类算法，具有计算效率高、可解释性强、鲁棒性强等优点。逻辑回归在信用评估、医疗诊断、电商推荐、舆情分析等应用场景中有广泛的应用。在实现逻辑回归模型时，可以使用现有的机器学习库或自己编写代码实现。