【算法实践】| 一步步手把手带你实现寻找最小公倍数

前言

其实最小公倍数的概念和计算最小公倍数的方法.那是我们在学习小学数学的时候就已经掌握的数学知识,为了更加通俗易懂一点,本文先从一个'分元宝'的故事入手:

亡故的先父留下遗嘱，

共有遗产17个元宝，

老大得元宝的二分之一、 17/2=8.5

老二得元宝的三分之一、 17/3=5.66666

老三得元宝的九分之一、 17/9=1.8

问他们每一个人分别应该分几个元宝？

在《一代大商孟洛川》中是这样做的

孟洛川拿来一个元宝加上去

好了，现在分元宝

答案是：老大9个元宝、老二6个元宝、老三2个元宝。

还剩下一个元宝，是我们孟洛川的，拿回来

很不可思议吧

很简单的初中数学题老大分1/2,老二分1/3,老三分1/9

这三个数的最小公倍数就是18,即9/18+6/18+2/18=17/18,就是说他们老爷子给的这个比例和根本就没到1,。即1-17/18=1/18,也就是说，直接分，那是分不完17元宝的。这样这要用18这个最小公倍数就能分开，最后还剩一个

很多人说数学学会四则混合运算就够了.其他买菜又用不到,这不,如果没有数学思维,连财产都分不明白(哈哈哈~),并不是除了四则混合运算其他数学知识没有用,而是我们没有学会或者不加以思考.其实很多时候我们在不知不觉中就已经使用了很多数学方法解决生活中所遇到的问题,所以学习数学,除了数学本身,还有数学思维的培养.言归正传,从上面的故事可看出最小公倍数对我们生产生活是有很大帮助的.故事中的例子就是分数的加减法运算在生活中的实际应用

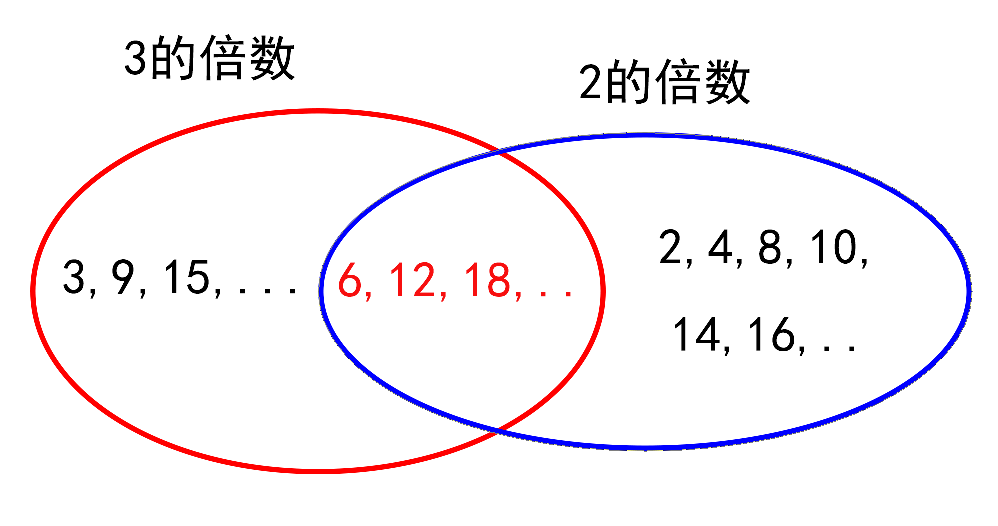
概念

在上篇文章《【算法实践】| 一步步带你实现寻找最大公约数》中我们浅尝了最大公约数的计算,那最大公约数有没有什么联系呢？

最大公约数往往是和最小公倍数成对出现的.最小公倍数（Least Common Multiple，缩写L.C.M.），如果有一个自然数a能被自然数b整除，则称a为b的倍数，b为a的约数，对于两个自然数来说，指该两数共有倍数中最小的一个。计算最小公倍数时，通常会借助最大公约数来辅助计算。

如果一个数既是a又是b的倍数，那么我们就把这个数叫着a和b的公倍数，如果这个数在a b的所有公倍数里为最小，那这个数就是最小公倍数。

通俗点说，几个数共有的倍数叫做这几个数的公倍数，其中除0以外最小的一个公倍数，叫做这几个数的最小公倍数。自然数a、b的最小公倍数可以记作[a、b],自然数a、b的最大公约数（最大公因数）可以记作(a、b)，当(a、b)=1时,[a、b]= a×b。如果两个数是倍数关系，则它们的最小公倍数就是较大的数，相邻的两个自然数的最小公倍数是它们的乘积。

简单概括如下：

最小公倍数：两个或多个整数公有的倍数叫做它们的公倍数，其中除0以外最小的一个公倍数就叫做这几个整数的最小公倍数

最大公约数和最小公倍数二者关系：两个数之积=最小公倍数*最大公约数，这也可作为我们求解最小公倍数的入手点,但是解题时要避免和最大公约数问题混淆

还有另外一个入手点:

因为，素数(质数)是不能被1和自身数以外的其它数整除的数；素数X的N次方，是只能被X的N-1以下次方，1和自身数整除．

所以，在求A，B，C，D，E，…，Z的最小公倍数时，只需要把这些数分解为素数的N次方之间的乘积后，取各素因子的最高次方的乘积，就是这些数的最小公倍数．

适用范围

最小公倍数的适用范围：分数的加减法，中国剩余定理(正确的题在最小公倍数内有解，有唯一的解)

最小公倍数的计算方法

综上所述,求解最小公倍数有以下两种方法:

1.分解质因数法

先把这几个数的质因数写出来，最小公倍数等于它们所有的质因数的乘积，如果有几个质因数相同，则比较两数中哪个数有该质因数的个数较多，乘较多的次数即可。

2.公式法

由于两个数的乘积等于这两个数的最大公约数与最小公倍数的积。即（a，b）×[a，b]=a×b。所以，求两个数的最小公倍数，就可以先求出它们的最大公约数，然后用上述公式求出它们的最小公倍数。

计算流程

1.分解质因数(穷举法)

2.公式法

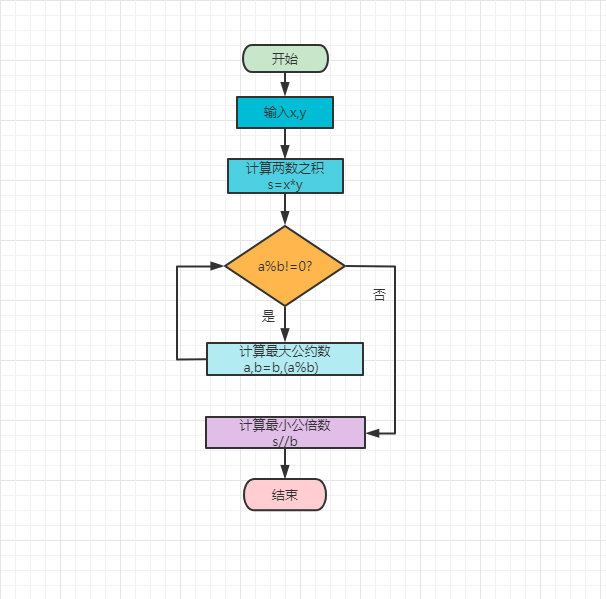
根据两者的关系,先计算最大公约数,然后使用公式计算最小公倍数

算法实现

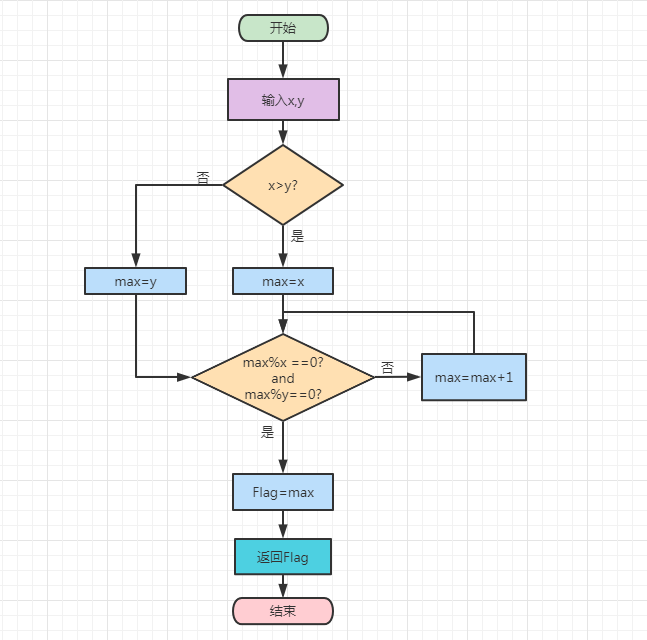
1.分解质因数的实现步骤:(穷举法)

1. 输入待求最小公倍数的两个整数x,y

2. 找出两个整数中较大的一个数字,并记录为max

3. 使用循环,判断max是否可以同时整除x和y,如果可以同时整除.退出循环,将max赋值给Flag,否则max加1,并且继续执行循环直到找到Flag

4. 返回Flag,即x与y的最小公倍数

代码如下:

方法1

def LCM(x,y):
    if x>y:
        max = x

    else:
        max = y

    while (True):
        if((max % x == 0) and (max % y == 0)):
            Flag = max
            break
        max = max + 1

    return Flag

x = int(input("请输入第一个整数:"))
y = int(input("请输入第二个整数:"))

print(x,",", y, "的最小公倍数为:", LCM(x,y))

执行结果如下:

方法2:

def lcm(x, y):
    #质因数分解
    Flag = 1
    i = 2
    while i <= min(x, y):
        if x % i == 0 and y % i == 0:
            Flag *= i
            x, y = x // i, y // i
        else:
            i += 1
    Flag = Flag * x * y
    return Flag

x = int(input("请输入第一个整数:"))
y = int(input("请输入第二个整数:"))

print(x,",", y, "的最小公倍数为:", lcm(x,y))

执行结果如下:

2.公式法具体实现步骤:

1. 输入待求最小公倍数的两个整数x,y

2. 计算两数的乘积s

3. 计算最大公约数x,y=y,(x%y)  

4. 根据公式两个数之积=最小公倍数*最大公约数,计算最小公倍数:s//y

5. 输出最小公倍数

具体实现代码如下:

x = int(input("请输入第一个整数:"))
y = int(input("请输入第二个整数:"))
s = x * y
while x % y != 0:
    x, y = y, (x % y)
else:
    print(x, ",", y, "的最大公约数为:",y)
    print(x, ",", y, "的最小公倍数为:",s // y)

执行结果如下: