【算法实践】| 一步步带你实现寻找最大公约数

前言

在实现之前我们先来了解一下什么是最大公约数，以及我们常用的计算最大公约数的方法或者说数学方法。

概念

最大公约数，也称最大公因数、最大公因子。他是一个能够被若干整数同时整除的整数，如果一个整数同时是几个整数的约数，则称这个整数为他们的公约数，公约数中最大的数成为最大公约数，1是任意若干的正整数的公约数。比如：一个数既是数A的约数，又是数B的约数，称为A,B的公约数，A,B的公约数中最大的一个（可以包括AB自身）称为AB的最大公约数，a，b的最大公约数记为（a，b），同样的，a，b，c的最大公约数记为（a，b，c），多个整数的最大公约数也有同样的记号。这么一大段可以概括为：

最大公约数：指两个或多个整数共有约数中最大的一个。

求最大公约数的方法

常见的有质因数分解法、短除法、辗转相除法、更相减损法。与最大公约数相对应的概念是最小公倍数，a，b的最小公倍数记为[a，b]。（先埋个小彩蛋：下一篇文章我们可以接着探索一下最小公倍数的计算方法）

短除法和辗转相除法是我们在数学解题中常用的两种方法。而且短除法也是我们在求二进制数时常用的方法，辗转相除法求可用来求解不定方程的一组整数解，这是它在数学中最常见的应用，辗转相除法处理大数时非常高效，它需要的步骤不会超过较小数的位数(十进制下)的五倍（加百利·拉梅(GabrielLamé)于1844年证明了这点，开创了计算复杂性理论）。辗转相除法的运算速度为 O(n)，其中 n 为输入数值的位数。

求解流程

本文通过穷举法和辗转相除法这两种个方法来寻找最大公约数。下面我们来看看两种的方法的具体流程：

穷举法流程图

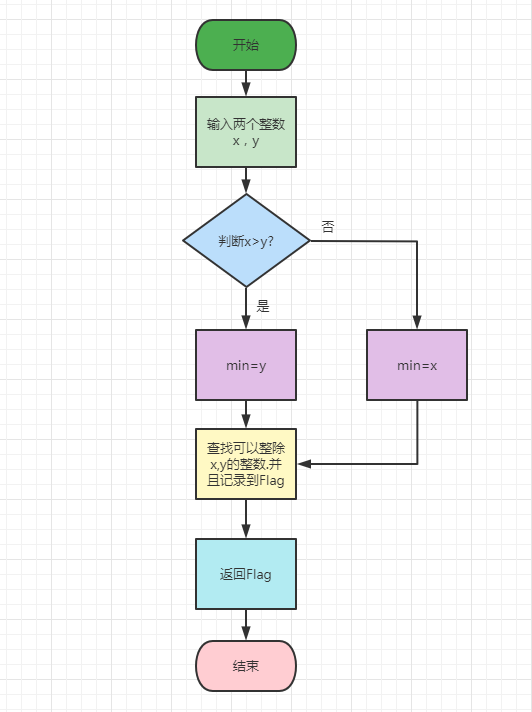
辗转相除法流程图

辗转相除法终止条件是 余数=0

除数是最小公约数

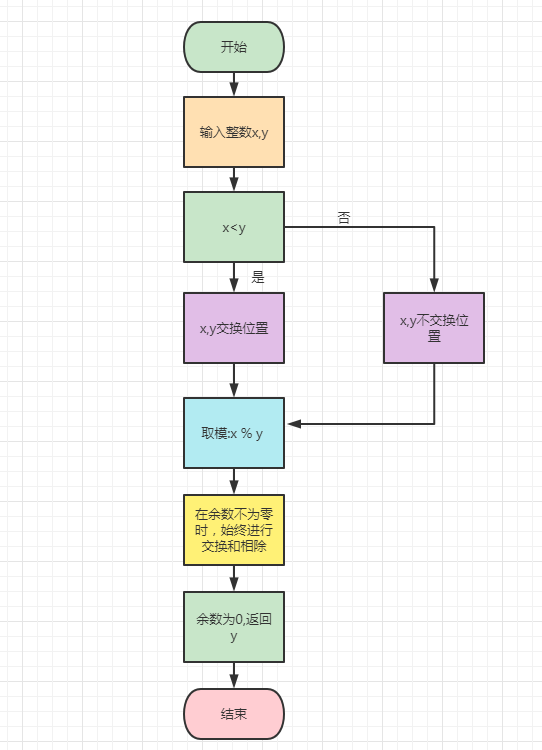
算法实现

穷举法

步骤:

1. 输入两个正整数

2. 找到其中较小的数,并记录为min

3. 使用穷举法,查找可以整除x,y两个值的数字,并记录为Flag.Flag小的值会被大的值覆盖掉

4. 返回Flag,就是x和y最大的公约数

代码如下:

def Findgcd(x,y):
    if x < y:
        min = y
    else:
        min = x

    for i in range(1, min+1):
        if((x % i == 0) and (y % i == 0)):
            Flag = i

    return Flag

x = int(input("请输入第一个整数:"))
y = int(input("请输入第二个整数:"))

print(x,",", y, "的最大公约数为:", Findgcd(x,y))

执行结果如下:

辗转相除法

1. 如果a<b，则交换两数位置，否则不交换

2. 求a/b的余数

3. 在余数不为零时，始终进行交换和相除

4. 余数为零后，打印输出b

代码如下:

x = int(input("请输入第一个整数:"))
y = int(input("请输入第二个整数:"))

if x < y: #如果x<y，则交换两数位置，否则不交换
    x,y = y,x
r = x % y
while r != 0: #在余数不为零时，不断进行交换和相除
    x,y = y,r
    r = x % y

print(x,",", y, "的最大公约数为:",y)

执行结果如下:

辗转相除法优化

1.递归

def gcd(x , y):
    if y == 0:
        return x
    else:
        return gcd(y, x%y)

a = int(input("请输入第一个整数:"))
b = int(input("请输入第二个整数:"))
print(x,",", y1, "的最大公约数为:",gcd(a,b))

2.非递归

x = int(input("请输入第一个整数:"))
y = int(input("请输入第二个整数:"))
y1  = y;
while y:
    x,y=y,x%y

print(x,",", y1, "的最大公约数为:",x)