1、线段树的概念

线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。使用线段树可以快速的查找某一个节点在若干条线段中出现的次数，时间复杂度为 $O(logN)$。而未优化的空间复杂度为 $2N$，实际应用时一般还要开 $4N$的数组以免越界，因此有时需要离散化让空间压缩。

我们可以基于一维数组来实现线段树，就跟完全二叉树的实现方式类似，假设当前节点为i,

左孩子节点下标： $leftChild=2*i+1$

右孩子节点下标： $rightChild=2*i+2$

本文参考B站视频：数据结构】线段树（Segment Tree）

2、线段树的操作

2.1 构建线段树

假设我们现在有如下数组： $arr=[1,3,5,7,9,11]$

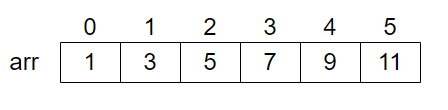
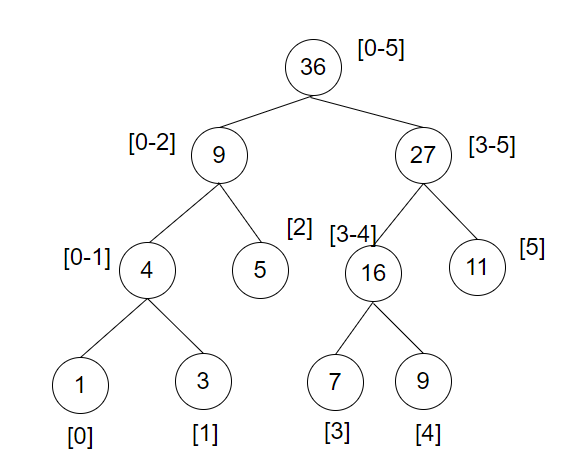
基于arr构建线段树，我们根节点存储的是区间[0-5]的和，再往下面分叉，左边表示[0-2]的和，右边表示[3-5]的和，以此类推，最后所有的叶子节点就是数组中的所有数字。最终构建的线段树如下：

保存这个线段树：我们使用一个数组保存，先标记上各个节点的下标，根节点下标为0，根节点的左孩子下表为 $2*0+1=1$，右孩子下标为 $2*0+2=2$,依次类推。

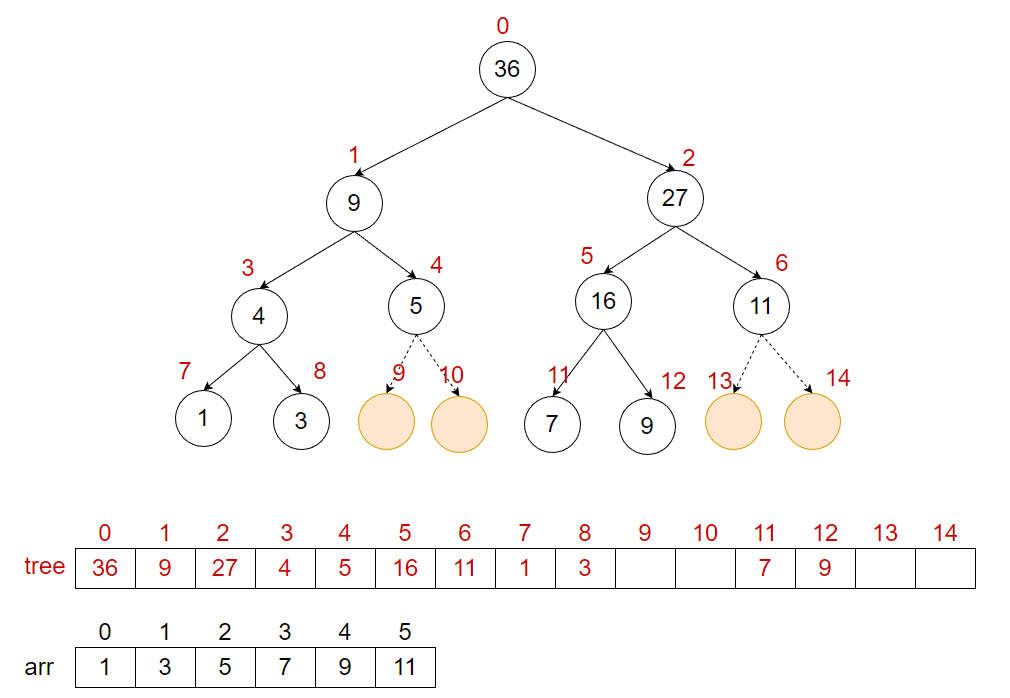
每个节点存储的都是其左孩子和右孩子的和。

这里代码使用递归实现比较好理解

  /**
     * 构建树
     * @param arr 原始数组
     * @param tree 线段树数组
     * @param node 当前节点下标
     * @param start 当前节点对应区间的左边界
     * @param end	当前节点对应区间的右边界
     */
    public static void buildTree(int[] arr, int[] tree, int node, int start, int end){
        if(start==end){//
            tree[node]=arr[start];
        }else{
            int mid=(start+end)/2;//从mid将区间分为两半
            int leftNode=2*node+1;//计算左孩子
            int rightNode=2*node+2;//计算右孩子
            //构建左子树
            buildTree(arr,tree,leftNode,start,mid);
            //构建右子树
            buildTree(arr,tree,rightNode,mid+1,end);
            //子树构建好之后，更新父节点的值
            tree[node]=tree[leftNode]+tree[rightNode];
        }
    }

2.2 单点修改

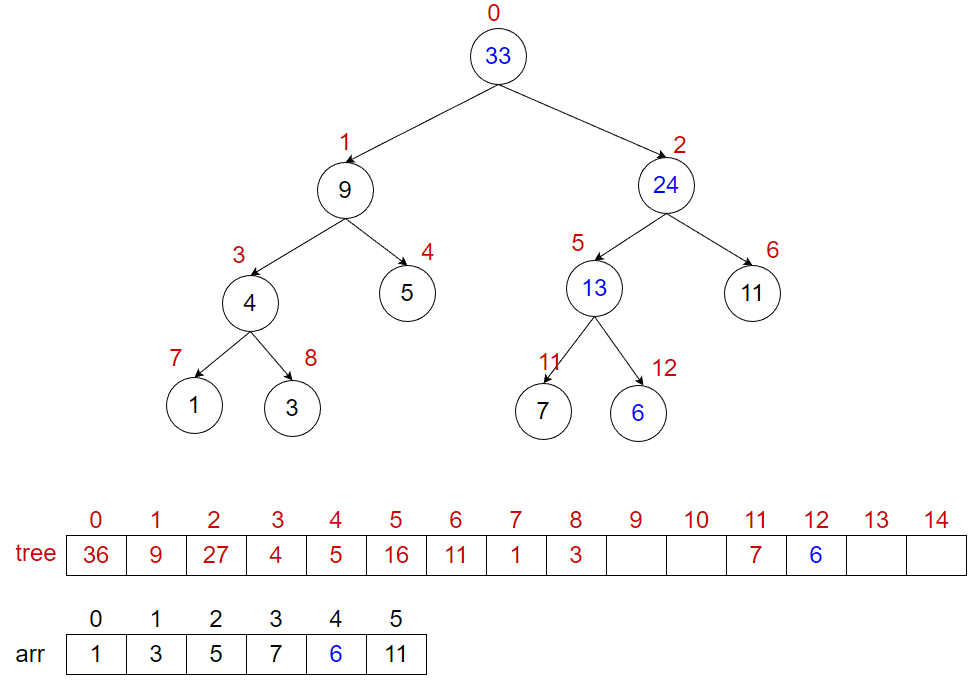
我们判断要修改的点是位于线段树的左子树还是右子树，若是左子树，递归左子树，修改对应节点的值，若是右子树那就递归右子树，修改对应节点的值。

修改完成之后还要修改父节点的值,假设我们现在想让 $arr[4]=6$,如下图所示。

 /**
     * 单点修改：想要将arr[index]=val，修改tree对应位置的值
     * @param arr
     * @param tree
     * @param node 当前节点下标
     * @param start 当前节点对应区间的左边界
     * @param end   当前节点对应区间的右边界
     * @param index 需要更新节点的下标(arr中的下标)arr[index]=val
     * @param val 修改后的值
     */
    public static void updateTree(int[] arr,int[] tree,int node,int start,int end,int index,int val){
        if(start==end){
            arr[index]=val;
            tree[node]=val;
        }else{
            int mid=(start+end)/2;
            int leftNode=2*node+1;
            int rightNode=2*node+2;
            if(index>=start&&index<=mid){   //要修改的值在左子树中
                updateTree(arr,tree,leftNode,start,mid,index,val);
            }else{  //要修改的值在右子树中
                updateTree(arr,tree,rightNode,mid+1,end,index,val);
            }
            //更新父节点的值
            tree[node]=tree[leftNode]+tree[rightNode];
        }
    }

2.3 区间查询

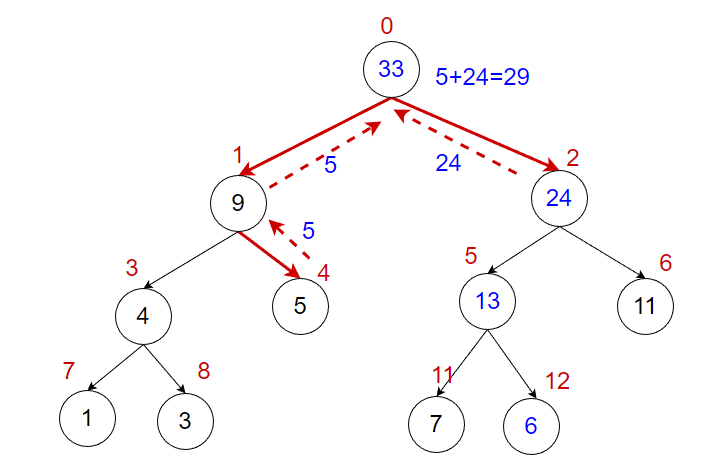
假设我们现在要查询区间 $[2-5]$的和，

• 先查询左子树 $[0-2]$,再查询右子树 $[2-2]$,满足 $(start==end)$，直接返回 $tree[4]=5$。

• 查询右子树 $[3-5]$，由于 $[3-5]$存在区间覆盖(节点2就是区间 $3-5$的和)，所以满足条件L<=start&&end<=R，直接返回 $tree[2]=24$（我们在2.2中修改了值）

• 再将左子树和右子树的结果求和: $5+24=29$

//区间查询：查询L-R区间的和
    public static int queryTree(int[] arr,int[] tree,int node,int start,int end,int L,int R){
        if(R<start||L>end){ //要查询的区间不在查询的范围之内
            return 0;
        } else if(L<=start&&end<=R){    //是否区间覆盖，可以直接返回tree[node]
            return tree[node];
        }else if(start==end){   //一直查到了叶子节点
            return tree[node];
        }else{
            int mid=(start+end)/2;
            int leftNode=2*node+1;
            int rightNode=2*node+2;
            //查询左子树
            int sumLeft=queryTree(arr,tree,leftNode,start,mid,L,R);
            //查询右子树
            int sumRight=queryTree(arr,tree,rightNode,mid+1,end,L,R);
            //将左右子树的结果相加即可
            return sumLeft+sumRight;
        }
    }

2.4 完整代码

package study.线段树;

import javax.xml.transform.Source;
import java.util.Arrays;

public class SegTree {
    public static final int MAX_LEN=1000;

    public static void main(String[] args) {
        int[] arr={1,3,5,7,9,11};
        int size=arr.length;
        int[] tree=new int[MAX_LEN];

        buildTree(arr,tree,0,0,size-1);
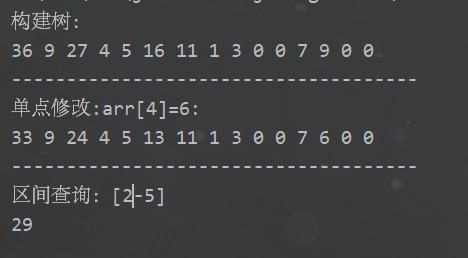
        System.out.println("构建树：");
        Arrays.stream(tree).limit(15).forEach(x-> System.out.print(x+" "));
        System.out.println("\n-------------------------------------");
        //修改测试
        updateTree(arr,tree,0,0,size-1,4,6);
        System.out.println("单点修改:arr[4]=6:");
        Arrays.stream(tree).limit(15).forEach(x-> System.out.print(x+" "));
        System.out.println("\n-------------------------------------");
        //查询测试
        System.out.println("区间查询：[2-5]");
        int sum = queryTree(arr, tree, 0, 0, size - 1, 2, 5);
        System.out.println(sum);

    }

    /**
     * 构建树
     * @param arr 原始数组
     * @param tree 线段树数组
     * @param node  当前节点下标
     * @param start
     * @param end
     */
    public static void buildTree(int[] arr, int[] tree, int node, int start, int end){
        if(start==end){//
            tree[node]=arr[start];
        }else{
            int mid=(start+end)/2;//从mid将区间分为两半
            int leftNode=2*node+1;//计算左孩子
            int rightNode=2*node+2;//计算右孩子
            //构建左子树
            buildTree(arr,tree,leftNode,start,mid);
            //构建右子树
            buildTree(arr,tree,rightNode,mid+1,end);
            //子树构建好之后，更新父节点的值
            tree[node]=tree[leftNode]+tree[rightNode];
        }
    }
    /**
     * 单点修改：想要将arr[index]=val，修改tree对应位置的值
     * @param arr
     * @param tree
     * @param node 当前节点下标
     * @param start 当前节点对应区间的左边界
     * @param end   当前节点对应区间的右边界
     * @param index 需要更新节点的下标(arr中的下标)arr[index]=val
     * @param val 修改后的值
     */
    public static void updateTree(int[] arr,int[] tree,int node,int start,int end,int index,int val){
        if(start==end){
            arr[index]=val;
            tree[node]=val;
        }else{
            int mid=(start+end)/2;
            int leftNode=2*node+1;
            int rightNode=2*node+2;
            if(index>=start&&index<=mid){   //要修改的值在左子树中
                updateTree(arr,tree,leftNode,start,mid,index,val);
            }else{  //要修改的值在右子树中
                updateTree(arr,tree,rightNode,mid+1,end,index,val);
            }
            //更新父节点的值
            tree[node]=tree[leftNode]+tree[rightNode];
        }
    }
    //区间查询：查询L-R区间的和
    public static int queryTree(int[] arr,int[] tree,int node,int start,int end,int L,int R){
        if(R<start||L>end){ //要查询的区间不在查询的范围之内
            return 0;
        } else if(L<=start&&end<=R){    //是否区间覆盖，可以直接返回tree[node]
            return tree[node];
        }else if(start==end){   //一直查到了叶子节点
            return tree[node];
        }else{
            int mid=(start+end)/2;
            int leftNode=2*node+1;
            int rightNode=2*node+2;
            //查询左子树
            int sumLeft=queryTree(arr,tree,leftNode,start,mid,L,R);
            //查询右子树
            int sumRight=queryTree(arr,tree,rightNode,mid+1,end,L,R);
            //将左右子树的结果相加即可
            return sumLeft+sumRight;
        }
    }
}