数据挖掘：降低汽油精制过程中的辛烷值损失模型(二)

举报
Lingxw_w 发表于 2023/04/27 15:34:05 2023/04/27
【摘要】 ​目录一、选取主要特征操作变量 1.1问题分析1.2 特征降维1.2.1低方差滤波1.2.2灰色关联分析 1.3 初步RFC模型1.3.1 导入相关的数据库1.3.2 构建初步随机森林模型1.3.3 GridSearch实现参数调优1.4 特征提取1.4.1 获取影响辛烷值的特征重要性 1.4.2 可视化变量的重要性一、选取主要特征操作变量 1.1问题分析汽油的实际精制生产工序十分繁琐，可操...

​目录

一、选取主要特征操作变量 

1.1问题分析

1.2 特征降维

1.2.1低方差滤波

1.2.2灰色关联分析 

1.3 初步RFC模型

1.3.1 导入相关的数据库

1.3.2 构建初步随机森林模型

1.3.3 GridSearch实现参数调优

1.4 特征提取

1.4.1 获取影响辛烷值的特征重要性

 1.4.2 可视化变量的重要性


一、选取主要特征操作变量 

1.1问题分析

汽油的实际精制生产工序十分繁琐，可操作位点繁多，而不同操作位点之间可能存在着某些相关性质，例如装置内部温度的变化可能会导致装置内部压力的变化。同时也存在 一些与汽油成品质量相关性不大的常规操作变量。为了降低后续数据处理过程中所消耗的计算资源，需要对354个操作变量进行筛选，使得筛选出的操作变量最具代表性，与目标输出指标的相关程度高。

数据来源：原始数据采集来源于中石化高桥石化实时数据库(霍尼韦尔 PHD)及 LIMS 实验数据库。

问题要求：附件一中提供的 325 个样本数据中，包括 7 个原料性质、2 个待生吸附剂 性质、2 个再生吸附剂性质、2 个产品性质等变量以及另外 354 个操作变量(共计 367 个 变量)。对上述 367 个变量进行降维，选出不超过 30 个特征变量对模型进行建模。要求 选择具有代表性、独立性。

目标：由于附件一中的 325 个样本的原料性质均有差异，故本文将样本的 7 个原料性质作为模型输入的一部分，且对单个样本进行分析时原料性质不可进行操作更改。此外，本文将对 367 个操作变量进行特征选择，从中选择 10 个对模型输出影响较大的操作变量作为降维后的特征。综上所述，本文对上述 367 个变量(其中预先确定选择 7 个原料属性变量)选择合适的特征降维方法进行降维后，得到共 17 个特征。

1.2 特征降维

http://t.csdn.cn/SJDJ6 12种降维方法终极指南

1.2.1低方差滤波

该方法假设数据列变化非常小的列包含的信息量少。因此，所有的数据列方差小的列被移除。需要注意的一点是：方差与数据范围相关的，因此在采用该方法前需要对数据做归一化处理。

example1:

1、初始化VarianceThreshfold，指定阀值方差

2、调用fit_transform

from sklearn.feature_selection import VarianceThreshold

if __name__ == '__main__':
    data = [
        [1, 2, 3, 4, 5],
        [1, 7, 8, 9, 10],
        [1, 12, 13, 14, 15]
    ]
    # 示例化一个转化器类
    transfer = VarianceThreshold()  # `threshold` 用默认值 0
    # 调用 transfer.fit_transform
    data_final = transfer.fit_transform(data)
    print('返回结果为：', data_final)

'''
返回结果为： [[ 2  3  4  5]
 [ 7  8  9 10]
 [12 13 14 15]]
'''


import numpy as np
import pandas as pd

data1=pd.read_excel('ques2.xlsx')


#加载模块
from sklearn.preprocessing import StandardScaler
import warnings
warnings.filterwarnings("ignore") #过滤掉警告的意思
from pyforest import *
import pandas as pd
import numpy as np
from sklearn.preprocessing import MinMaxScaler
#区间缩放，返回值为缩放到[0, 1]区间的数据
Standard_data=MinMaxScaler().fit_transform(data1)

#由于标准化后的数据是array格式，故将其转化为数据框
Standard_data = pd.DataFrame(Standard_data) #转为dataframe
# 将文件写入excel表格中
writer = pd.ExcelWriter('Standard_data_ques2.xlsx')  #关键2，创建名称为hhh的excel表格
Standard_data.to_excel(writer,'page_1',float_format='%.5f')  #关键3，float_format 控制精度，将data_df写到hhh表格的第一页中。若多个文件，可以在page_2中写入
writer.save()  #关键4
S_data_ques2=pd.read_excel('Standard_data_ques2.xlsx')
from sklearn.feature_selection import VarianceThreshold

# 示例化一个转化器类
transfer = VarianceThreshold()  # `threshold` 用默认值 0
# 调用 transfer.fit_transform
data_final_1 = transfer.fit_transform(S_data_ques2)
print('返回结果为：', data_final_1)

data_df = pd.DataFrame(data_final_1)   #关键1，将ndarray格式转换为DataFrame
# 将文件写入excel表格中
writer = pd.ExcelWriter('new_ques2.xlsx')  #关键2，创建名称为hhh的excel表格
data_df.to_excel(writer,'page_1',float_format='%.5f')  #关键3，float_format 控制精度，将data_df写到hhh表格的第一页中。若多个文件，可以在page_2中写入
writer.save()  #关键4

处理之后的数据、变量缩减至211：

1.2.2灰色关联分析 

对于两个系统之间的因素，其随时间或不同对象而变化的关联性大小的量度，称为关联度。在系统发展过程中，若两个因素变化的趋势具有一致性，即同步变化程度较高，即可谓二者关联程度较高；反之，则较低。因此，灰色关联分析方法，是根据因素之间发展趋势的相似或相异程度，亦即“灰色关联度”，作为衡量因素间关联程度的一种方法。

灰色系统理论提出了对各子系统进行灰色关联度分析的概念，意图透过一定的方法，去寻求系统中各子系统（或因素）之间的数值关系。因此，灰色关联度分析对于一个系统发展变化态势提供了量化的度量，非常适合动态历程分析。

计算步骤

1、确实参考数列与比较数列

2、对参考数列与比较数列进行无量纲化处理

3、计算关联系数,求关联度

import pandas as p
import numpy as np
from numpy import *
import matplotlib.pyplot as plt
%matplotlib inline

# 从硬盘读取数据进入内存
data_2=pd.read_excel('RFC.xlsx')
data_2.head()

这里要把变量RON放在最后一列。 


# 无量纲化
def dimensionlessProcessing(df):
    newDataFrame = pd.DataFrame(index=df.index)
    columns = df.columns.tolist()
    for c in columns:
        d = df[c]
        MAX = d.max()
        MIN = d.min()
        MEAN = d.mean()
        newDataFrame[c] = ((d - MEAN) / (MAX - MIN)).tolist()
    return newDataFrame

def GRA_ONE(gray, m=0):
    # 读取为df格式
    gray = dimensionlessProcessing(gray)
    # 标准化
    std = gray.iloc[:, m]  # 为标准要素
    gray.drop(str(m),axis=1,inplace=True)
    ce = gray.iloc[:, 0:]  # 为比较要素
    shape_n, shape_m = ce.shape[0], ce.shape[1]  # 计算行列

    # 与标准要素比较，相减
    a = zeros([shape_m, shape_n])
    for i in range(shape_m):
        for j in range(shape_n):
            a[i, j] = abs(ce.iloc[j, i] - std[j])

    # 取出矩阵中最大值与最小值
    c, d = amax(a), amin(a)

    # 计算值
    result = zeros([shape_m, shape_n])
    for i in range(shape_m):
        for j in range(shape_n):
            result[i, j] = (d + 0.5 * c) / (a[i, j] + 0.5 * c)

    # 求均值，得到灰色关联值,并返回
    result_list = [mean(result[i, :]) for i in range(shape_m)]
    result_list.insert(m,1)
    return pd.DataFrame(result_list)


def GRA(DataFrame):
    df = DataFrame.copy()
    list_columns = [
        str(s) for s in range(len(df.columns)) if s not in [None]
    ]
    df_local = pd.DataFrame(columns=list_columns)
    df.columns=list_columns
    for i in range(len(df.columns)):
        df_local.iloc[:, i] = GRA_ONE(df, m=i)[0]
    return df_local
# 灰色关联结果矩阵可视化

import seaborn as sns

def ShowGRAHeatMap(DataFrame):
    colormap = plt.cm.RdBu
    ylabels = DataFrame.columns.values.tolist()
    f, ax = plt.subplots(figsize=(14, 14))
    ax.set_title('GRA HeatMap')
    
    # 设置展示一半，如果不需要注释掉mask即可
    mask = np.zeros_like(DataFrame)
    mask[np.triu_indices_from(mask)] = True
    
    with sns.axes_style("white"):
        sns.heatmap(DataFrame,
                    cmap="YlGnBu",
                    annot=True,
                    mask=mask,
                   )
    plt.show()
    
data_2_gra = GRA(data_2)
# 画出热力图
ShowGRAHeatMap(data_2_gra)

1.3 初步RFC模型

通过随机森林(RFC)模型对汽油辛烷值RON进行特征提取与模型优化。

1.3.1 导入相关的数据库

import matplotlib.pyplot as plt
from sklearn.ensemble import RandomForestClassifier     #随机森林用于分类
from sklearn.ensemble import RandomForestRegressor       #随机森林用于回归
from sklearn.model_selection import train_test_split           #划分训练集与测试集
from sklearn import metrics    
from sklearn.metrics import r2_score              #用于模型拟合优度评估
import numpy as np 
import pandas as pd           #读取数据

这里，产品辛烷值RON作为数据标签，其余作为特征，由于特征过多，需要对对特征进行降维提取。

#将数据分为训练和测试集
train_labels = df_2.iloc[:,0]          #数据标签
train_features= df_2.iloc[:,1:]        #数据特征
feature_list = list(train_features.columns)        #数据特征名称
train_features = np.array(train_features)            #格式转换
#划分训练集与测试集
train_features, test_features, train_labels, test_labels = train_test_split(train_features, train_labels, test_size = 0.25, random_state = 42)

1.3.2 构建初步随机森林模型

#构造随机森林模型
rf=RandomForestRegressor(n_estimators = 1000,oob_score = True,n_jobs = -1,random_state =42,max_features='auto',min_samples_leaf = 12)
rf.fit(train_features,train_labels)               #模型拟合
predictions= rf.predict(test_features)                 #预测
print("train r2:%.3f"%r2_score(train_labels,rf.predict(train_features)))         #评估
print("test r2:%.3f"%r2_score(test_labels,predictions))

初步构造未提取特征之前的随机森林模型，测试集与训练集结果展示如下： 

 可以看到，模型拟合训练集比测试集程度好，说明模型拟合程度待优化，这里通过网格搜索方法实现模型参数的优化。

1.3.3 GridSearch实现参数调优

from sklearn.model_selection import GridSearchCV
#GridSearch网格搜索 进行参数调优
rfc=RandomForestRegressor()
param = {"n_estimators": range(1,20),"min_samples_leaf": range(1,20)}     #要调优的参数
gs = GridSearchCV(estimator=rfc,param_grid=param,cv=5)
gs.fit(train_features,train_labels)                  #调优拟合

参数调优后就是进行模型最优参数导出:

#导出调参后最优参数
best_score=gs.best_score_
best_params=gs.best_params_
print(best_score,best_params,end='\n')

可以看到，模型拟合分数为0.65，再次对模型进行拟合查看参数调优后的效果。 

#最优参数再次进行模型评估
rf=RandomForestRegressor(n_estimators = 14,oob_score = True,n_jobs = -1,random_state =42,max_features='auto',min_samples_leaf = 5)
rf.fit(train_features,train_labels)
predictions= rf.predict(test_features)
print("train r2:%.3f"%r2_score(train_labels,rf.predict(train_features)))
print("test r2:%.3f"%r2_score(test_labels,predictions))

  可以看到，模型的训练集拟合优度大幅度提升，测试集模型额拟合优度也有明显额提升，但幅度不大。

1.4 特征提取

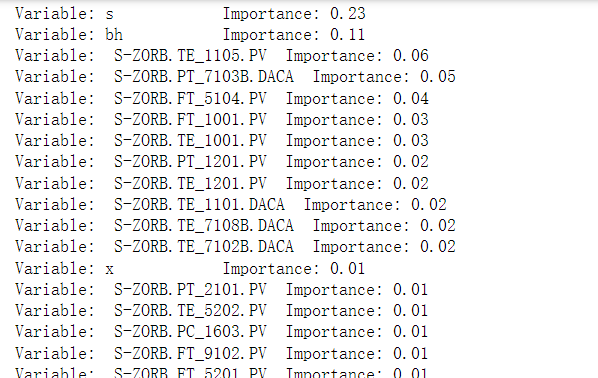
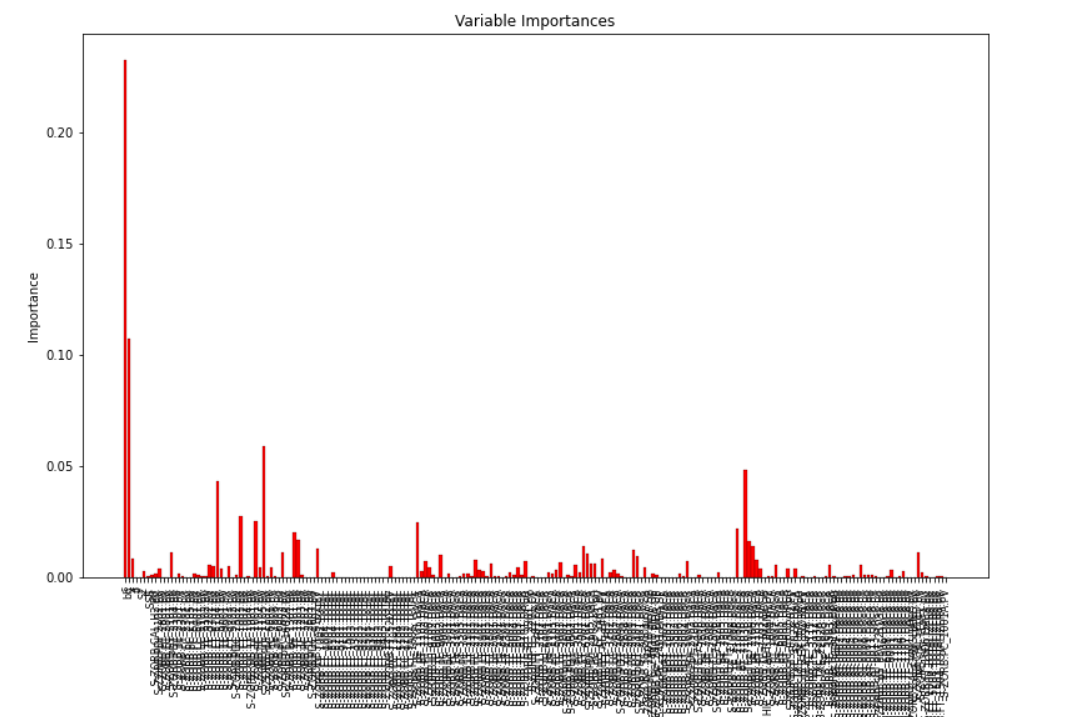
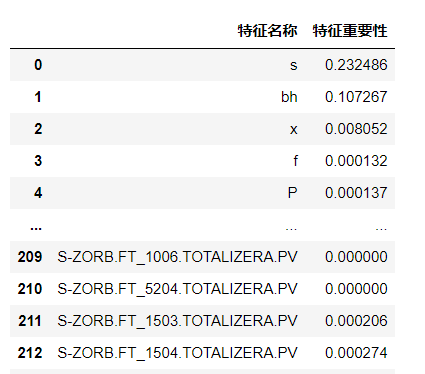
1.4.1 获取影响辛烷值的特征重要性

importances = list(rf.feature_importances_)      #辛烷值RON影响因素的重要性
feature_importances = [(feature, round(importance, 2)) for feature, importance in zip(feature_list,importances)]     #将相关变量名称与重要性对应
feature_importances = sorted(feature_importances, key = lambda x: x[1], reverse = True)                #排序
[print('Variable: {:12} Importance: {}'.format(*pair)) for pair in feature_importances]            #输出特征影响程度详细数据

 1.4.2 可视化变量的重要性

#绘图
f,ax = plt.subplots(figsize = (13,8))    #设置图片大小
x_values = list(range(len(importances)))     
plt.bar(x_values,importances, orientation = 'vertical', color = 'r',edgecolor = 'k',linewidth =0.2)    #绘制柱形图
# Tick labels for x axis
plt.xticks(x_values, feature_list, rotation='vertical',fontsize=8)      
# Axis labels and title
plt.ylabel('Importance'); plt.xlabel('Variable'); plt.title('Variable Importances');

# 以二维表格形式显示
importances_df = pd.DataFrame()
importances_df["特征名称"]=feature_list
importances_df["特征重要性"]=importances
p=importances_df.sort_values("特征重要性",ascending=False)
 print(importances_df)

​编辑 这里选择15个特征变量，并最终作为辛烷值RON的特征。

​

【版权声明】本文为华为云社区用户原创内容，转载时必须标注文章的来源（华为云社区）、文章链接、文章作者等基本信息， 否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱： cloudbbs@huaweicloud.com
数据挖掘 机器学习
  • 点赞
  • 收藏
  • 关注作者

评论（0）

0/1000
抱歉，系统识别当前为高风险访问，暂不支持该操作

全部回复

上滑加载中

设置昵称

在此一键设置昵称，即可参与社区互动！

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

*长度不超过10个汉字或20个英文字符，设置后3个月内不可修改。

确认 取消

加入云驻计划，成为创作者

  • 华为云周边好礼
  • 免费体验产品
  • 特殊身份标识
  • 线下官方门票
  • 内部专家零距离
  • 与10000+优质创作者共同成长
立即加入