机器学习:K-means算法基本原理及其变种
目录
1.1、K-means起源
美1967年,James MacQueen在他的论文《用于多变量观测分类和分析的一些方法》中首次提出 “K-means”这一术语。1957年,贝尔实验室也将标准算法用于脉冲编码调制技术。1965年,E.W. Forgy发表了本质上相同的算法——Lloyd-Forgy算法,所以这一算法有时也被称为Lloyd-Forgy算法。更高效的版本则被Hartigan and Wong提出。
K-means聚类算法被提出来后,在不同的学科领域被广泛研究和应用,并发展出大量不同的改进算法。虽然K-means聚类算法被提出已经超过50年了,但目前仍然是应用最广泛的划分聚类算法之—。容易实施、简单、高效、成功的应用案例和经验是其仍然流行的主要原因。
1.2、K-means的意义
K-means算法已经被国内外学者研究多年,并且在商业、工业、科学、人工智能、统计学等很多领域广泛应用,如用于商业银行客户信息细分、微博热点词汇挖掘、图形分割等。
K-means算法是基于距离的聚类算法,具有算法思想简单、收敛速度快、对大规模数据集的处理效率高、对凸形或球形分布的数据集聚类效果好等特点。
1.3、K-means的思想
经典K-means算法的基本思想是:给定一个需要进行聚类分析统计的数据集S,假设有n个数据对象,输入一个参数A的值;其次,从数据集S中随机选择A个样本对象作为初始聚类中也,将集合中剩余数据对象按照某种相似性度量规则(一般用欧氏距离)划分到离其最近的中也点代表的集合,形成A个类簇;然后,重新计算形成的每个簇的中心,根据新的中心重新划分其他数据对象;不断迭代以上过程,每次迭代重新调整数据对象的划分,当邻近两次聚类的划分过程中所有样本都不再调整类别或者聚类目标函数达到了收敛的条件时,则说明所有数据对象都已经被正确划分了,此时聚类过程结束。
k-mean又叫k均值算法,它是一种聚类算法,聚类算法在机器学习中属于无监督的学习算法(Unsupervised Learning),其中k表示聚类后类别的个数,k是人为预先指定的。
这里,我们也许会想几个问题:
(1)k的值是人为的选取,有没有一套科学指导方法? 往往给定一个数据集,我们事先并不知道应该要把该数据集划分成多少类才合适。
(2)如何对数据集划分呢?对于其中的任何一条数据记录,我们该把它归为k类中的哪一类?
(3)如何知道最后得到的聚类结果是好还是坏呢?也就是说有没有一个标准去测试聚类结果的好坏。
带着这些问题我们先看看聚类算法的核心思想:给定一个数据集,它有n条数据记录,我们要把它分为k类,那么最后这k类中类之间的相似度最小,类内的相似度到达最大。
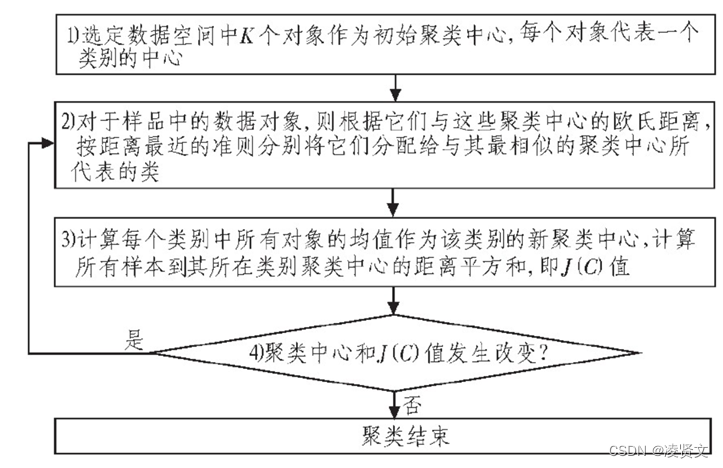
1.4、K-means的算法流程
图1.1算法流程图
1.选择聚类的个数k(k-means算法传递超参数的时候,只需设置最大的K值)
2.任意产生k个聚类,然后确定聚类中心,或者直接生成k个中心。
3.对每个点确定其聚类中心点。
4.再计算其聚类新中心。
5.重复以上步骤直到满足收敛要求。(通常就是确定的中心点不再改变。)
1.5、K-means的算法优缺点
优点:
1、原理简单(靠近中心点) ,实现容易
2、聚类效果中上(依赖K的选择)
3、空间复杂度o(N),时间复杂度o(IKN)
N为样本点个数,K为中心点个数,I为迭代次数
缺点:
1、对离群点, 噪声敏感 (中心点易偏移)
2、很难发现大小差别很大的簇及进行增量计算
3、结果不一定是全局最优,只能保证局部最优(与K的个数及初值选取有关)
2.1、轮廓系数
(Silhouette Coefficient)结合了聚类的凝聚度(Cohesion)和分离度
(Separation),用于评估聚类的效果。该值处于-1~ 1之间,值越大,表示聚类效果越好。
a是Xi与同簇的其他样本的平均距离,称为凝聚度;b是Xi与最近簇中所有样本的平均距离,称为分离度。
最近簇的定义:
其中p是某个簇Ck中的样本。即,用Xi到某个簇所有样本平均距离作为衡量该点到该簇的距离后,选择离Xi最近的一个簇作为最近簇。
求出所有样本的轮廓系数后再求平均值就得到了平均轮廓系数。平均轮廓系数的取值范围为[-1,1],且簇内样本的距离越近,簇间样本距离越远,平均轮廓系数越大,聚类效果越好。
代码实现:
对于一个聚类任务,我们希望得到的簇中,簇内尽量紧密,簇间尽量远离,轮廓系数便是类的密集与分散程度的评价指标,公式表达如下: s=b−amax(a,b)s=b−amax(a,b) 其中a代表同簇样本到彼此间距离的均值,b代表样本到除自身所在簇外的最近簇的样本的均值,s取值在[-1, 1]之间。 如果s接近1,代表样本所在簇合理,若s接近-1代表s更应该分到其他簇中。
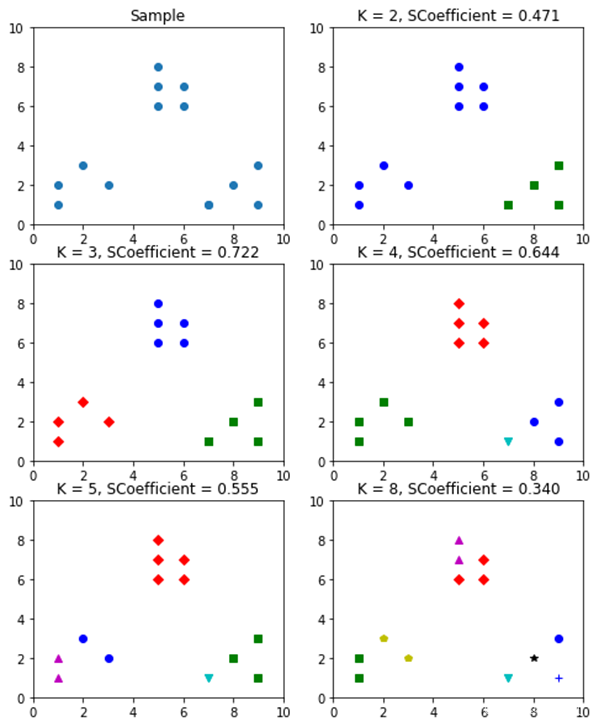
判断: 轮廓系数范围在[-1,1]之间。该值越大,越合理。 si接近1,则说明样本i聚类合理; si接近-1,则说明样本i更应该分类到另外的簇; 若si 近似为0,则说明样本i在两个簇的边界上。 所有样本的si 的均值称为聚类结果的轮廓系数,是该聚类是否合理、有效的度量。使用轮廓系数(silhouette coefficient)来确定,选择使系数较大所对应的k值。
图2.1
图2.2
2.2、k值的确定
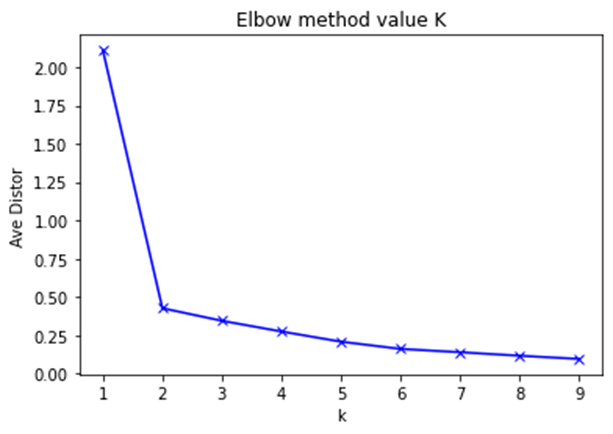
Elbow method就是“肘”方法,对于n个点的数据集,迭代计算k from 1 to n,每次聚类完成后计算每个点到其所属的簇中心的距离的平方和,可以想象到这个平方和是会逐渐变小的,直到k==n时平方和为0,因为每个点都是它所在的簇中心本身。但是在这个平方和变化过程中,会出现一个拐点也即“肘”点,下图可以看到下降率突然变缓时即认为是最佳的k值。
我们知道K-means是以最小化样本与质点平方误差作为目标函数,将每个簇的质点与簇内样本点的平方距离误差和称为畸变程度(distortions),那么,对于一个簇,它的畸变程度越低,代表簇内成员越紧密,畸变程度越高,代表簇内结构越松散。 畸变程度会随着类别的增加而降低,但对于有一定区分度的数据,在达到某个临界点时畸变程度会得到极大改善,之后缓慢下降,这个临界点就可以考虑为聚类性能较好的点。
给出肘部法则来确定k值的代码:
输出结果:
[2.108866682672935, 0.42817162051875596, 0.3461215687887749, 0.27647951702531254, 0.20999507473469947, 0.16292773202223396, 0.1412500679328461, 0.11845062955323304, 0.09749934879787367]
图2.3
- 最常用最简单的方法可视化数据,然后观察出聚类聚成几类比较合适
- 绘制出k-average with cluster distance to centroid的图表,观察随着k值的增加,曲线的下降情况,当曲线不再“急剧”下降时,就是合适的k值
- 计算不同k值下KMeans算法的BIC和AIC值,BIC或AIC值越小,选择该k值
- 使用 Canopy算法先进行粗略的聚类,产生的簇的个数,作为KMeans算法的k值
- 使用x-means方法结合BIC准则去判定簇的个数,也就是k值
- 使用Gap Statistic公式来确定k值
- 使用轮廓系数来确定,选择使系数较大所对应的k值
- 使用交叉验证来确定使目标函数(距中心的距离的平方差)变小的k值
- 利用Affinity propagation的方法估计最优的聚类数目,进一步进行KMeans的算法
- 利用层次聚类,可视化后认为地观察认定可聚为几类,确定k值
- 确定较粗的数目,并找到一个初始聚类,然后用迭代重定位来改进该聚类。
由下表可以看出
缺点 |
改进 |
k的选取不好把握 |
ISODATA |
对初始聚类中心敏感 |
K-means++ |
对非凸数据集比较难收敛 |
DESCAN |
若数据类型不平衡,则聚类效果不佳 |
CUSBoost |
采用的是迭代的方法,容易陷入局部最优 |
二分K-means |
对于噪音和异常点比较敏感 |
K-Mediods |
3.1、K-means++
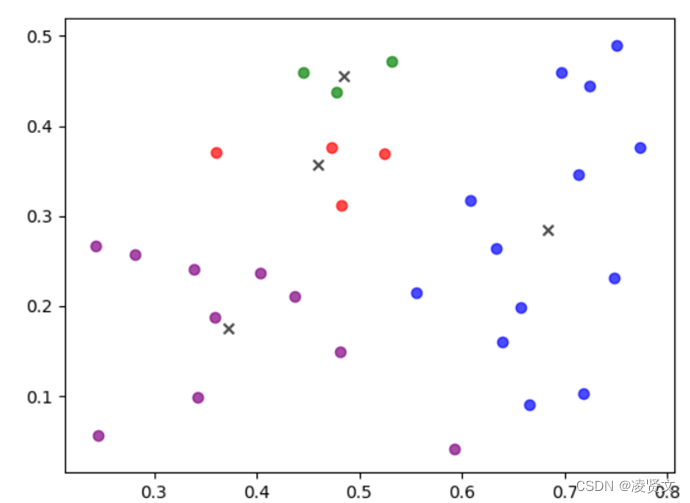
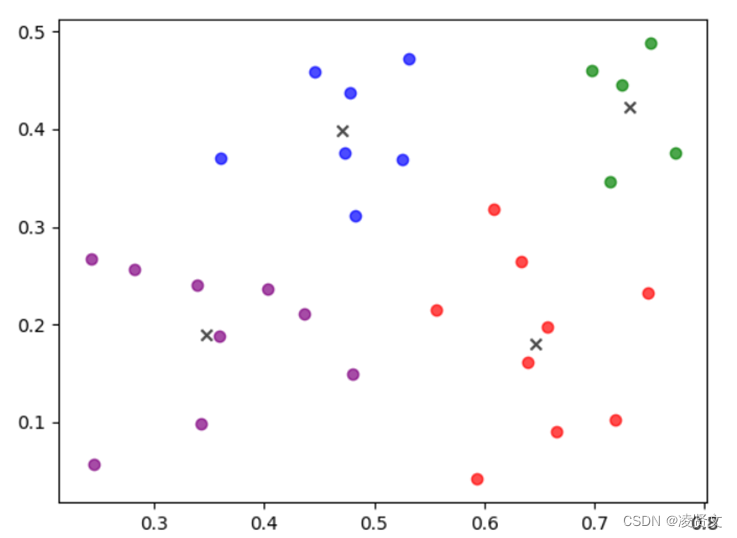
K-means在初始化聚类中心时是在最小值和最大值之间随机取一个值作为其聚类中心,这样的随机取值会导致聚类中心可能选择的不好,最终对结果会产生很大的影响。经过测试,如果样本类别区分度较明显,按照K-means初始化聚类中心,对结果的影响并不大;反之,如果样本的类别区分度不大,聚类结果会有较大的不同。下面用周志华老师的《机器学习》这本书里的西瓜数据集来说明。
图3.1
图3.2
上述两张图可以说明,对于同一数据集,不同的初始聚类中心其产生的结果会有较大的不同。因此,K-means++算法被提出了
K-means++算法是K-means算法的改进版,主要是为了选择出更优的初始聚类中心。其基本思路如下:
在数据集中随机选择一个样本作为第一个初始聚类中心;
选择出其余的聚类中心:
计算数据集中的每一个样本与已经初始化的聚类中心之间的距离,并选择其中最短的距离,记为di,以概率选择距离最大的样本作为新的聚类中心,重复上述过程,直到k个聚类中心都被确定。
对k个初始的聚类中心,利用K-means算法计算出最终的聚类中心。
3.2、ISODATA
ISODATA算法是在k-均值算法的基础上,增加对聚类结果的“合并”和“分裂”两个操作,并设定算法运行控制参数的一种聚类算法。迭代次数会影响最终结果,迭代参数选择很重要。
3.3、Kernel K-means
“kernel方法是一类用于模式分析或识别的算法,其最知名的使用是在支持向量机(SVM)。模式分析的一般任务是在一般类型的数据(例如序列,文本文档,点集,向量,图像等)中找到并研究一般类型的关系(例如聚类,排名,主成分,相关性,分类)图表等)。内核方法将数据映射到更高维的空间,希望在这个更高维的空间中,数据可以变得更容易分离或更好的结构化。对这种映射的形式也没有约束,这甚至可能导致无限维空间。然而,这种映射函数几乎不需要计算的,所以可以说成是在低维空间计算高维空间内积的一个工具。”
主要思想是通过一个非线性映射,将输入空间中的数据点映射到高维特征空间中,在特征空间中进行聚类。
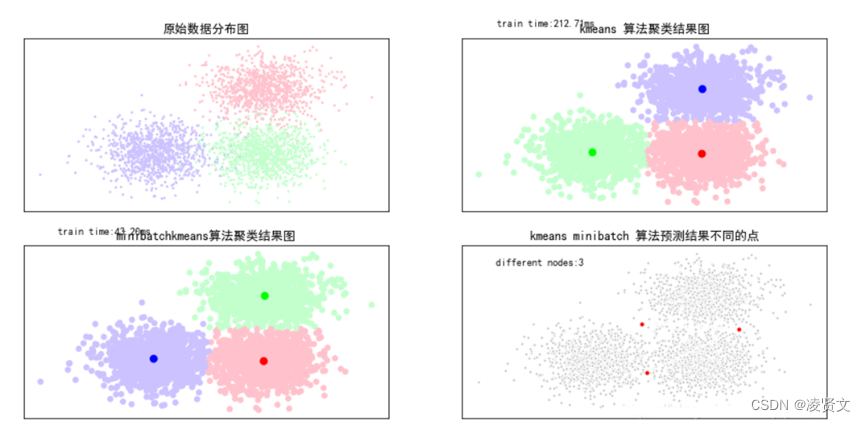
3.4、Mini Batch K-means
Mini Batch K-means算法是K-means算法的一种优化变种,采用小规模的数据子集(每次训练使用的数据集是在训练算法的时候随机抽取的数据子集)减少计算时间,同时试图优化目标函数;Mini Batch K-means算法可以减少K-means算法的收敛时间,而且产生的结果效果只是略差于标准K-means算法
算法步骤如下:
·首先抽取部分数据集,使用K-means算法构建出K个聚簇点的模型
·继续抽取训练数据集中的部分数据集样本数据,并将其添加到模型中,分配给距离最近的聚簇中心点·更新聚簇的中心点值(每次更新都只用抽取出来的部分数据集)
·循环迭代第二步和第三步操作,直到中心点稳定或者达到迭代次数,停止计算操作
MiniBatchKMeans类的主要参数比KMeans类稍多,主要有:
1) n_clusters: 即我们的k值,和KMeans类的n_clusters意义一样。
2)max_iter:最大的迭代次数, 和KMeans类的max_iter意义一样。
3)n_init:用不同的初始化质心运行算法的次数。这里和KMeans类意义稍有不同,KMeans类里的n_init是用同样的训练集数据来跑不同的初始化质心从而运行算法。而MiniBatchKMeans类的n_init则是每次用不一样的采样数据集来跑不同的初始化质心运行算法。
4)batch_size:即用来跑Mini Batch KMeans算法的采样集的大小,默认是100.如果发现数据集的类别较多或者噪音点较多,需要增加这个值以达到较好的聚类效果。
5)init: 即初始值选择的方式,和KMeans类的init意义一样。
6)init_size: 用来做质心初始值候选的样本个数,默认是batch_size的3倍,一般用默认值就可以了。
7)reassignment_ratio: 某个类别质心被重新赋值的最大次数比例,这个和max_iter一样是为了控制算法运行时间的。这个比例是占样本总数的比例,乘以样本总数就得到了每个类别质心可以重新赋值的次数。如果取值较高的话算法收敛时间可能会增加,尤其是那些暂时拥有样本数较少的质心。默认是0.01。如果数据量不是超大的话,比如1w以下,建议使用默认值。如果数据量超过1w,类别又比较多,可能需要适当减少这个比例值。具体要根据训练集来决定。
8)max_no_improvement:即连续多少个Mini Batch没有改善聚类效果的话,就停止算法, 和reassignment_ratio, max_iter一样是为了控制算法运行时间的。默认是10.一般用默认值就足够了。
图3.3
K-means算法是一种十分优秀的聚类算法,以其简单的算法思想、较快的聚类速度和良好的聚类效果得到了广泛的应用。对于该算法在聚类过程中暴露出的若千问题,本文对其中K值确定、初始聚类中心选择以及分类属性数据处理等主要问题进行了总结。
自从K-Means算法提出以来,不断有学者提出改进算法,丰富K-Means算法内容。K-Means算法是一个十分经典的聚类算法,其今后的应用也将会越来越普遍。对于传统K-Means算法中存在的一些缺点以及针对这些缺点的改进方法,文中进行了详细的阐述。
K-Means算法有着广泛的应用前景,今后也将面临更多的挑战。对K-Means算法的改进绝不止于本文中所阐述的方向。总结前人的经验,未来针对K-Means算法还可以对以下方向进行研究:(1)提升K-Means算法处理海量或多维数据集的能力。随着大数据时代的到来,所能获取的信息量呈指数式爆炸,如何将K-Means更好地用于处理指数级数据的聚类,也是需要研究的方向。(2)降低K-Mleans算法的时间复杂度。改进的K-Mleans聚类算法有着良好的聚类效果,但这是在牺牲了时间的前提下换来的,如何能更好更快地提升聚类能力,需要做更进一步优化。
- 点赞
- 收藏
- 关注作者

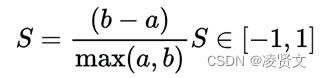
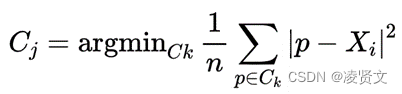


评论(0)