
01、随机变量
有些随机实验的结果是用数值表示的,有些不是。当实验结果不是用数值表示时,很难对其进行描述和研究,所以有必要将实验结果数值化,这便是引入随机变量的初衷。
【例1】将一枚硬币抛掷三次,观察正面和反面出现的情况,样本空间是S={HHH,HHT,HTH,THH,HTT,THT,TTH,TTT}。以X记三次投掷得到正面H的总数,那么,对于样本空间S中的每一个样本点e,X都有一个数与之对应。X是定义在样本空间S上的一个实值单值函数,它的定义域是样本空间S,值域是实数集合{0,1,2,3}。这样的X称为随机变量。
代码如下:


运行结果如图1所示。

■ 图1
注释/
numpy.random.RandomState()是一个伪随机数生成器,和设置seed的效果是一样的。
随机变量按其取值情况可分为离散型随机变量与连续型随机变量。离散型随机变量的取值可以一一列举,连续型随机变量的取值不能一一列举。
01、离散型随机变量及其分布律
要掌握一个离散型随机变量X的统计规律,必须且只须知道X的所有可能取值以及取每个可能值的概率。本节引入 scipy的stats子模块介绍离散型随机变量。
首先引入stats,查看stats包含哪些离散型随机变量的分布,代码如下:

运行结果如图2所示。

■ 图 2
这里列出了15种离散型分布,仅介绍其中的三种——bernoulli,binom,poisson。
- 0-1分布
0-1分布也叫伯努利(Bernoulli)分布。设随机变量X只可能取两个值0和1,它的分布律是:

则称X服从参数为p的(0-1)分布或伯努利分布。scipy中bernoulli()对应(0-1)分布,代码如下:

运行结果如图3所示。

运行结果如图4所示。

- 二项分布
设X为n重伯努利实验中某事件A发生的次数,X可取k=0,1,2,…,n。若P(A)=p,则X的分布律为:

称X服从参数为n,p的二项分布。scipy中binom对应二项分布,使用方法代码如下:

运行结果如图5所示。

■ 图 5
注释/
pmf是概率质量函数。rv服从参数为5,0.3的二项分布,rv. pmf(x)返回随机变量rv取值为0,1,2,3,4,5时的概率值,与使用分布律公式算得的值是一致的,代码如下:

运行结果如图6所示。

■ 图6
【例2】某种型号电子元件的使用寿命如果超过1500小时,则为一级品。已知某一大批产品的一级品率为0.2,现在从中随机地抽查20只。问20只元件中恰有k只(k=0,1,…,10)为一级品的概率是多少?
解由题意可得,20只元件中一级品的只数服从参数为20,0.2的二项分布,所求概率代码如下:

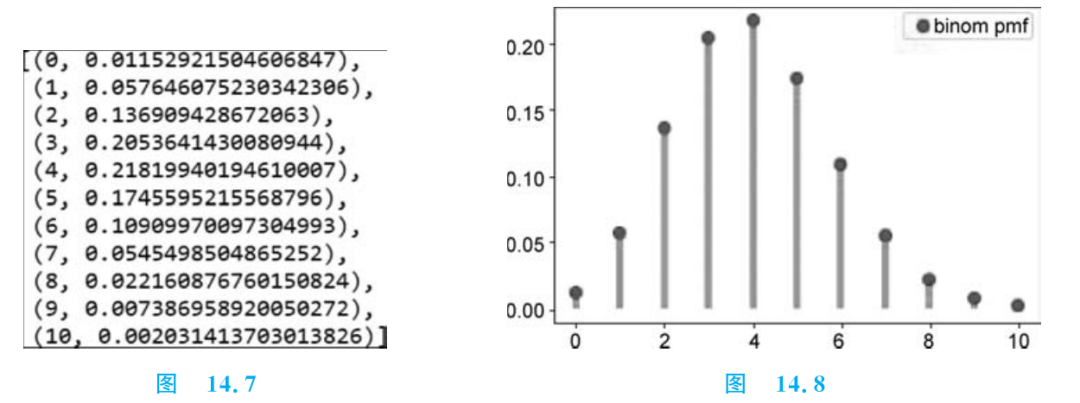
运行结果如图7所示。
进一步,可作上述结果的图形,以便对该结果有一个直观的了解,代码如下:

运行结果如图8所示。

注释/
(1) subplots()函数返回一个包含figure和axes对象的元组,因此,使用fig,ax=plt.subplots()将元组分解为fig和ax两个变量。fig变量可用来修改figure层级的属性,ax变量中保存着子图的可操作axes对象。
(2) ax.plot(x,rv.pmf(x),'ro',ms=8,label='binom pmf')使用红色圆圈标记绘制x与rv.pmf(x),标记大小为8,标签为binom pmf。
(3) ax. vlines(x,0,rv.pmf(x),colors='g',lw=5,alpha=0.5)在x处绘制从0到rv. pmf(x)的垂直线,线条颜色为绿色,线条宽度为5,透明度为0.5。
从图形输出结果可以看到,当k增加时,相应概率先是随之增加,增大到最大值(k=4时)后单调减少。
【例3】某人进行射击,设每次射击的命中率为0.02,独立射击400次,试求至少击中两次的概率。
解代码如下:

运行结果如图9所示。

■ 图9
- 泊松分布
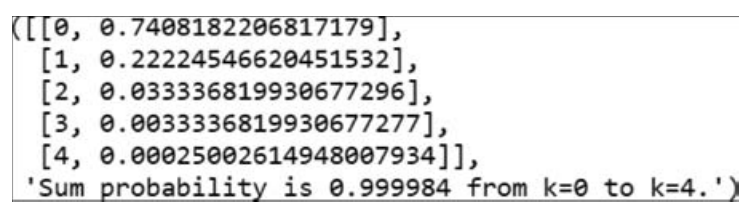
设随机变量X所有可能的取值为0,1,2,…,取各个值的概率为

其中,λ>0是常数。则称X服从参数为λ的泊松分布。scipy中poisson对应泊松分布,代码如下:
运行结果如图10所示。

■ 图 10
【例4】某公司制造一种特殊型号的微芯片,次品率达0.1%,各芯片成为次品相互独立。求在1000只产品中至少有2只次品的概率。
解由题可知,产品中的次品数服从参数为n=1000,p=0.001的二项分布,这里n很大,p很小,该二项分布可用参数为n、p的泊松分布来逼近,我们尝实验证这一结论,代码如下:

运行结果如图11所示。

■ 图 11
从输出结果可以看到,两种分布下所得概率相差无几。







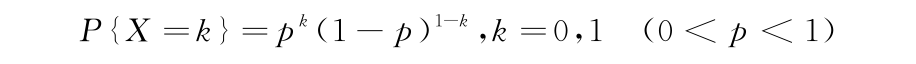



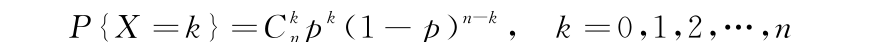


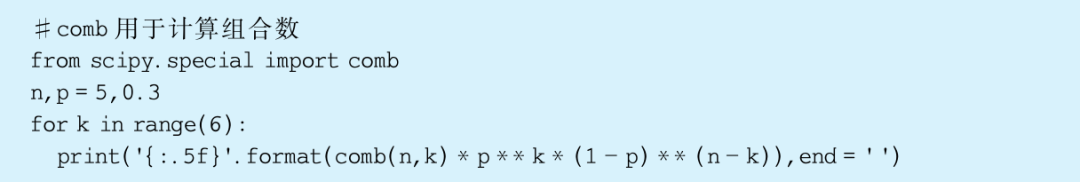
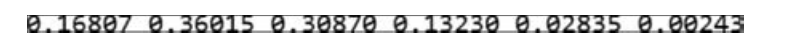



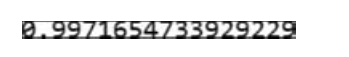
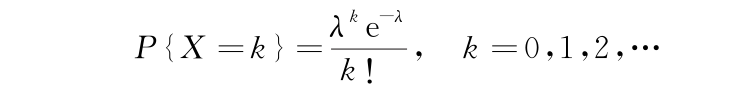

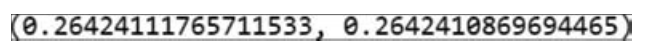

评论(0)