@toc

1、问题描述

对于一个长度为 N 的整数数列 $A_1,A_2,...A_N$, 小蓝想知道下标 l 到 r 的部分和$ {\textstyle \sum_{i=l}^{r}}=A_1+A_{l+1}+…+A_r $ 是多少?

然而, 小蓝并不知道数列中每个数的值是多少, 他只知道它的M个部分和的值。其中第 i 个部分和是下标 $l_i$ 到 $r_i$的部分和$ {\textstyle \sum_{j=l_i}^{r_i}}=A_{l_i}+A_{l_i+1}+…+A_{r_i} $, 值是$s_i$。

输入格式

第一行包含 3 个整数N*、M 和 Q 。分别代表数组长度、已知的部分和数量 和询问的部分和数量。

接下来 M 行, 每行包含 3 个整数 $l_i,r_i,S_i$。

接下来 Q 行, 每行包含 2 个整数 l 和 r, 代表一个小蓝想知道的部分和。

输出格式

对于每个询问, 输出一行包含一个整数表示答案。如果答案无法确定, 输出 UNKNOWN。

样例输入

5 3 3
1 5 15
4 5 9
2 3 5
1 5
1 3
1 2

样例输出

15
6
UNKNOWN

评测用例规模与约定

对于 10% 的评测用例,1≤N,M,Q≤10,−100≤ $S_i$≤100 。

对于 20% 的评测用例, 1≤N,M,Q≤20,−1000≤ $S_i$≤1000 。

对于 30% 的评测用例, 1≤N,M,Q≤50,−10000≤ $S_i$≤10000 。

对于 40% 的评测用例, 1≤N,M,Q≤1000,−106≤ $S_i$≤ $10^6$ 。

对于 60% 的评测用例, 1≤N,M,Q≤10000,−109≤ $S_i$≤ $10^9$。

对于所有评测用例, 1≤N,M,Q≤ $10^5$, $-10^{12}$≤ $S_i$≤ $10^{12}$,1≤ $l_i$≤ $r_i$≤N, 1≤l≤r≤N 。数据保证没有矛盾。

运行限制

• 最大运行时间：3s
• 最大运行内存: 512M

2、解题思路(带权并查集)

这个需要先了解并查集的概念，我之前写过一篇并查集的文章，链接如下：

并查集(Union-find Sets)

我们之前使用的并查集主要处理一些不相交集合的合并及查询问题，即询问某两个节点是否在同一个集合。

但是带权并查集除了描述集合之间的关系外，还用权值来表示当前节点与根节点的相对关系。

2.1 带权并查集核心操作

2.1.1 查找操作(路径压缩)

查找节点x的根节点的时候，压缩x节点到根节点的路径，这样我们下一次查找x的根节点时候，至于要一步操作就能；在查找的时候也要更新x的权值，这个权值就代表了x到根节点的路径长度。

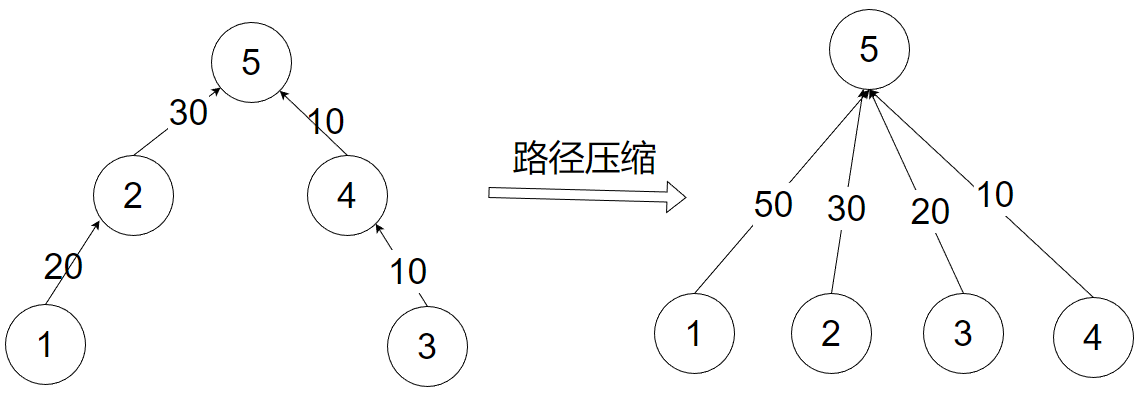
上图为路径压缩操作的示意图，可以看到，压缩之后，我们可以在 $O(1)$的复杂度内找到当前节点到根节点的边权值，同样如果要计算部分和的话也非常方便。

比如我们现在要计算1到3的部分和，那我们直接用 $1\sim 5$的边权值减去 $3\sim 5$的边权值=50-20=30

//带权并查集查找操作(路径压缩)
public static int findFather(int x){
    if(father[x]!=x){
        int tmp = father[x];
        father[x]=findFather(father[x]);//找根节点
        value[x]+=value[tmp];   //压缩路径
    }
    return father[x];
}

2.1.2 合并操作

假设我们现在已经知道了 $1\sim2$和 $3\sim5$的部分和，现在要将节点1所在的连通图与节点3所在的连通图合并，现在给出 $1\sim3$的权值为20。

合并的时候，我们需要将2指向5，假设 $2->5$的权值为L,则我们可以知道， $1-2-5$的权值和 $1-3-4-5$的权值应该是相等的，有

$10+L=s+10+20$

则 $L=-10+s+10+20$

//带权并查集合并操作
public static void union(int left,int right,long s){
    int leftFather = findFather(left);
    int rightFather = findFather(right);
    if(leftFather!=rightFather) {
        //合并x和y的集合，并更新权值
        //合并规则，将小根节点集合指向大根节点集合
        int small = Math.min(leftFather, rightFather);
        int big = Math.max(leftFather, rightFather);
        father[small]=big;
        value[small]=Math.abs(-value[left]+value[right]+s);
    }
}

2.2 带权并查集代码实现(AC)

对于本题来说，我们需要将区间的左端点从0开始，在计算部分和的时候我们不包括左端点的值,如果求1到2位置上的部分和时，若并查集结构为(1->2)，此时1到2之间就只能有一个权值，即只能指导1或者2位置上的值，所以并查集的结构应改为(0->1->2)。

比如我们要求 $1\sim2$的部分和时，此时 $0\sim1$的边权值表示的是1位置上的值， $1\sim 2$的边权值表示的是2位置上的值，此时求1到2位置上的部分和时，即 $0\sim 1\sim 2$路径的权值和。

import java.io.*;

/**
 * 推导部分和：带权并查集
 * 本题中，区间左端点从0开始，计算部分和的时候不包括左端点的值
 * 原因：求1到2位置上的部分和时，若并查集结构为(1->2)，此时1到2之间就只能有一个权值，
 * 即只能指导1或者2位置上的值，所以并查集的结构应改为(0->1->2)
 * 即(0->1)的边权值是表示1位置的值，(1->2)的边权值表示2位置的值
 * 此时求1到2位置上的部分和时，即(0->1->2)路径的权值和
 */
public class Main {
    //记录每个节点的父节点
    public static int[] father;
    //value[i]表示i到其根节点的路径长度
    public static long[] value;
    public static StreamTokenizer st=new StreamTokenizer(new BufferedReader(new InputStreamReader(System.in)));
    public static PrintWriter out=new PrintWriter(new BufferedWriter(new OutputStreamWriter(System.out)));
    public static void main(String[] args) throws IOException {
        int N = nextInt();    //数组长度
        int M = nextInt();    //已知的部分和数量
        int Q = nextInt();    //询问的部分和数量
        father=new int[N+1];
        init(N);
        value = new long[N + 1];

        //已知的部分和
        for (int i = 0; i <M; i++) {
            int left = nextInt();
            int right = nextInt();
            long s = nextLong();
            left--;
            union(left,right,s);
        }
        //询问的部分和
        for (int i = 0; i <Q ; i++) {
            int left = nextInt();
            int right = nextInt();
            left--;
            int leftFather = findFather(left);
            int rightFather = findFather(right);
            if(leftFather!=rightFather){
                out.println("UNKNOWN");
            }else{
                out.println(value[left]-value[right]);
            }
        }
        out.flush();
        out.close();
    }
    //带权并查集初始化
    public static void init(long n){
        for (int i = 0; i <=n; i++) {
            father[i]=i;    //初始的时候父节点都指向自己
        }
    }
    //带权并查集查找操作(路径压缩)
    public static int findFather(int x){
        if(father[x]!=x){
            int tmp = father[x];
            father[x]=findFather(father[x]);//找根节点
            value[x]+=value[tmp];   //压缩路径
        }
        return father[x];
    }
    //带权并查集合并操作
    public static void union(int left,int right,long s){
        int leftFather = findFather(left);
        int rightFather = findFather(right);
        if(leftFather!=rightFather) {
            //合并x和y的集合，并更新权值
            //合并规则，将小根节点集合指向大根节点集合
            int small = Math.min(leftFather, rightFather);
            int big = Math.max(leftFather, rightFather);
            father[small]=big;
            value[small]=Math.abs(-value[left]+value[right]+s);
        }
    }

    public static int nextInt() throws IOException{
        st.nextToken();
        return (int)st.nval;
    }
    public static long nextLong() throws IOException{
        st.nextToken();
        return (long)st.nval;
    }
}

思路参考：

蓝桥杯2022第十三届—推导部分和（带权并查集的应用）

第十三届蓝桥杯JavaA组、C++A组省赛 J 题——推导部分和 (AC)