@toc

1、题目描述

小明有一个容量为V的背包。

这天他去商场购物，商场一共有N件物品，第i件物品的体积为 $w_i$,价值为 $v_i$。

小明想知道再购买的物品总体积不超过V的情况下所能获得的最大价值为多少，请你帮他算算。

输入描述

输入第1行包含两个正整数N,V，表示商场物品的数量和小明的背包容量。

第 $2\sim N+1$行每行包含两个正整数w,v,表示物品的体积和价值。

$$1\le N\le10^2,1\le V\le10^3,1\le w_i,v_i\le10^3$$

输出描述

输出一行整数表示小明所能获得的最大价值。

输入输出样例

输入

5 20
1 6
2 5
3 8
5 15
3 3

输出

37

2、示例分析

我们用一个简单的实例去分析，我们假设当前物品描述如下：

我们有4件物品，背包容量为8，我们的目标是求在背包容量为8的前提下能装物品的最大价值。

定义f(k,w)为：当背包容量为w，现在有k件物品可以偷，所能偷到的最大价值。

所以我们的目标就是求f(4,8)

分析如下：

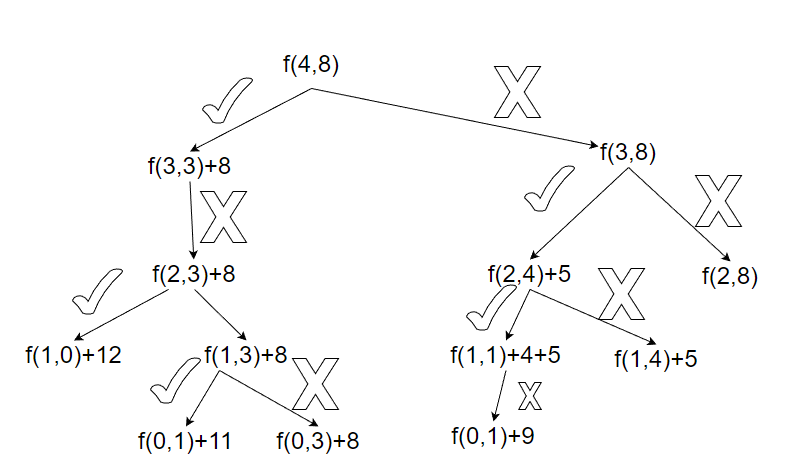
上图中带 $\surd$表示选了第k件物品， $\times$表示没选第k件物品。

如果拿了第4件物品，那么 $f(4,8)$就转化为拿了前3件物品的情况，此时 $f(4,8)=f(3,8-5)+8$

如果没拿第4件物品，那么 $f(4,8)=f(3,8)$,因为没拿第4件，所以背包容量没变。

得出状态转移方程：

$$f(k,w)=\left\{\begin{matrix} f(k-1,w),w_k>w,(太重，装不下) \\ max[f(k-1,w),f(k-1,w-w_k)+v_k],w_k<=w \end{matrix}\right.$$

当 $w_k<=w$时， $f(k-1,w)$代表没拿第k件物品， $f(k-1,w-w_k)+v_k$代表拿了第k件物品。

我们可以将所有的计算结果写成表格。

这里f(0,w)表示不拿物品，价值肯定为0，f(k,0)表示被包装量为0，肯定装不下，所以第一行和第一列都是0，这里算几个关键的。

$f(1,2)=max[f(0,0)+3,f(0,2)]=max[3,0]=3$

$f(2,3)=max[f(1,3-3)+4,f(1,3)]=max[4,3]=4$

$f(2,4)=max[f(1,4-4)+4,f(1,4)]=max(4,3)=4$

$f(2,5)=max[f(1,5-3)+4,f(1,5)]=max[f(1,2)+4,f(1,5)]=max[7,3]=7$

这里只给出一部分的计算过程

3、代码实现

import java.util.Scanner;

//小明的背包
public class Bag {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int N = scan.nextInt(); //物品数量
        int V = scan.nextInt(); //背包容量
        int[] w = new int[N + 1];//物品体积
        int[] v = new int[N + 1];//物品价值
        //记录最优解,我们的目标是f[N][V]
        int[][] f = new int[N + 1][V + 1];
        for (int i = 1; i <=N; i++) {
            w[i]=scan.nextInt();
            v[i]=scan.nextInt();
        }
        for (int i = 1; i <=N; i++) {	//i代表N件物品
            for (int j = 1; j <=V; j++) {	//j表示背包容量
                if(w[i]>j){ //太重，装不下
                    f[i][j]=f[i-1][j];
                }else{
                    //f[i][j]=max{不拿第i件，拿第i件}
                    f[i][j]=Math.max(f[i-1][j],f[i-1][j-w[i]]+v[i]);
                }
            }
        }
        System.out.println(f[N][V]);
    }
}