@toc

上一篇博客讲解了BFS广度优先搜索求解迷宫问题，今天试试DFS深度优先搜索

1、题目描述

给定一个 $N\times M$的网格迷宫G。G的每个格子要么是道路，要么是障碍物(道路用1表示，障碍物用2表示)。

一直迷宫的入口位置为 $(x_1,y_1)$，出口位置为 $(x_2,y_2)$。问从入口道出口，最多要走多少个格子。

输入描述

输入第1行包含两个整数N,M，分别表示迷宫的大小

接下来输入一个 $N \times M$的矩阵。若 $G_{i,j}=1$表示其为道路，否则表示其为障碍物。

最后一行输入四个整数 $x_1,y_1,x_2,y_2$，表示入口的位置和出口的位置。

$$1\le N,M\le 10^2, 0\le G_{i,j}\le 1,1\le x_1,x_2\le N,1\le y_1,y_2\le M$$

输出描述

输出仅一行，包含一个整数表示答案。

若无法从入口道出口，则输出-1。

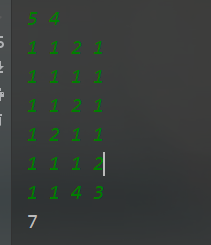
输入示例

5 4
1 1 2 1
1 1 1 1
1 1 2 1
1 2 1 1
1 1 1 2
1 1 4 3

输出示例

7

2、解题思路

初始迷宫如下图所示：

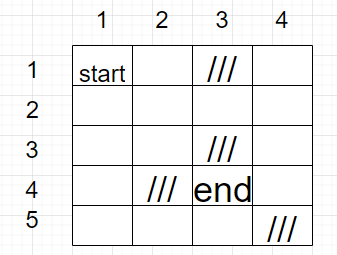
我们大致的想法如下：

• 先判断是否到达目标位置，如果达到目标位置，再试探有无其他更短的路径。
• 如果没有达到目标位置，则找到下一步可以到达的位置，直到找到目标位置。

我们需要先给出四个方向，并用如下代码代理上下左右四个方向

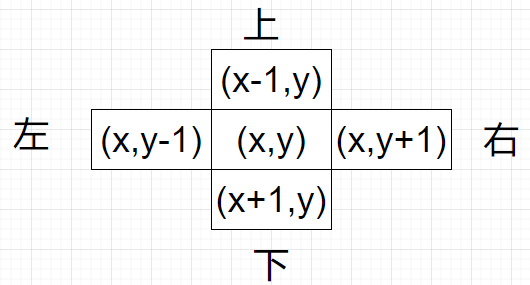
static int[][] dirs={
            {0,1},//右
            {1,0},//下
            {0,-1},//左
            {-1,0}//上
};

在这里我们规定按照顺时针方向(右、下、左、上)去一个个试探相邻的节点，我们试探到一个符合条件的节点，就继续按照顺时针方向接着进行试探，每经过一个节点，都要使用visited[x][y]=true数组来标记该节点已经被访问过。

如果我们搜索到了终点，此时还需要进行回溯，因为我们走的这条路不一定是路径最短的。回溯的时候每一个经过的节点的访问状态标记为未访问visited[x][y]=false，因为我们每次在搜索的时候都有个是否被访问过的判断，回溯的时候不标记为false，那后面就再过不来了。

经过尝试我们得到了下面三种方案

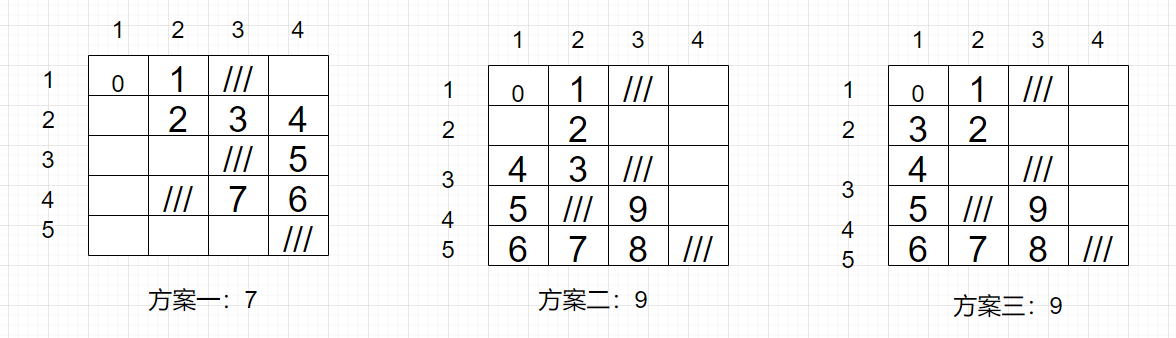
这里并没找全，因为手动模拟搜索再回溯很容易标错，这个需要你自己在草稿纸上模拟一下，这里要是过程与全部画出来未免显得不优雅。

3、代码实现

很明显，这里用递归的话可以减少很多代码量，非递归的写法我后面有时间再尝试下吧，普通版本代码如下：

public class Main {
    public static int endX;
    public static int endY;
    public static int min=Integer.MAX_VALUE; //最小路径长度
    //迷宫：1表示空地，2表示障碍物
    public static int[][] a=new int[100][100];
    //false表示未访问，true表示访问
    public static boolean[][] visited=new boolean[100][100];
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        //n行m列
        int n = scan.nextInt();
        int m = scan.nextInt();
        //初始化迷宫
        for (int i = 1; i <=n ; i++) {
            for (int j = 1; j <=m ; j++) {
                a[i][j]=scan.nextInt();//1表示空地，2表示障碍物
            }
        }
        //起点和终点坐标
        int startX = scan.nextInt();
        int startY = scan.nextInt();
         endX = scan.nextInt();
         endY = scan.nextInt();
        //从起点开始深度优先搜素，所以先将起点设置为已访问
        visited[startX][startY]=true;
        dfs(startX,startY,0);
        System.out.println(min);
    }

    /**
     * @param x 当前点的x坐标
     * @param y 当前点的y坐标
     * @param step 经过的步数
     */
    public static void dfs(int x,int y,int step){
        if(x==endX&&y==endY){   //判断是否走到终点
            if(step<min){   //如果比最短路径小，更新最短路径
                min=step;
            }
            return; //回溯
        }
        //顺时针试探：右、下、左、上
        //右
        if(a[x][y+1]==1&& !visited[x][y + 1]){  //是道路且没有被访问过
            visited[x][y+1]=true;   //将右边的点设置为已访问
            dfs(x,y+1,step+1);//继续从右边这个点进行深度优先搜索
            //当上一步dfs执行完，回退的时候需要将这个点设置为未访问
            visited[x][y+1]=false;
        }
        //下
        if(a[x+1][y]==1&& !visited[x + 1][y]){
            visited[x+1][y]=true;   //将下边的点设置为已访问
            dfs(x+1,y,step+1);//继续从下边这个点进行深度优先搜索
            //当上一步dfs执行完，回退的时候需要将这个点设置为未访问
            visited[x+1][y]=false;
        }
        //左
        if(a[x][y-1]==1&& !visited[x][y - 1]){
            visited[x][y-1]=true;   //将左边的点设置为已访问
            dfs(x,y-1,step+1);//继续从左边这个点进行深度优先搜索
            //当上一步dfs执行完，回退的时候需要将这个点设置为未访问
            visited[x][y-1]=false;
        }
        //上
        if(a[x-1][y]==1&& !visited[x-1][y]){
            visited[x-1][y]=true;   //将上边的点设置为已访问
            dfs(x-1,y,step+1);//继续从上边这个点进行深度优先搜索
            //当上一步dfs执行完，回退的时候需要将这个点设置为未访问
            visited[x-1][y]=false;
        }
        return;//回退
    }
}

这里的dfs函数中关于右、下、左、上四个方向的探索还能再优化，现在这样写存在大量看起来重复的代码。

不知道你发现了没有，上面这段代码我们并没有判断索引越界的情况它也没报错。因为我们if里面的判断条件一直是看是否等于1，visited[x][y]是否为false。而我们的二维数组a[100][100]默认初始化是全为0的，所以边界外的a[i][j]全为0，不符合条件。我们是a[1][1]走的，a[0][0]并没有使用，所以即使从起点向左向上也不会越界。

不明白就看下面这种优化后的，下面的代码加了边界判断思路会更清楚。

优化版本如下：

import java.util.Scanner;
public class Main {
    public static int endX;
    public static int endY;
    public static int min=Integer.MAX_VALUE; //最小路径长度
    //迷宫：1表示空地，2表示障碍物
    public static int[][] a;
    //false表示未访问，true表示访问
    public static boolean[][] visited;
    //定义四个方向
    public static int[][] dirs={
            {0,1},//右
            {1,0},//下
            {0,-1},//左
            {-1,0}//上
    };

    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        //n行m列
        int n = scan.nextInt();
        int m = scan.nextInt();
        a=new int[n+1][m+1];
        visited=new boolean[n+1][m+1];
        //初始化迷宫
        for (int i = 1; i <=n ; i++) {
            for (int j = 1; j <=m ; j++) {
                a[i][j]=scan.nextInt();//1表示空地，2表示障碍物
            }
        }
        //起点和终点坐标
        int startX = scan.nextInt();
        int startY = scan.nextInt();
         endX = scan.nextInt();
         endY = scan.nextInt();
        //从起点开始深度优先搜素，所以先将起点设置为已访问
        visited[startX][startY]=true;
        dfs1(startX,startY,0);
        System.out.println(min);

    }
   //优化版本
    public static void dfs1(int x,int y,int step){
        if(x==endX&&y==endY){   //判断是否走到终点
            if(step<min){   //如果比最短路径小，更新最短路径
                min=step;
            }
            return; //回溯
        }
        //顺时针试探：右、下、左、上
        for (int[] dir : dirs) {
            //计算出下一个试探位置
            int tx=x+dir[0];
            int ty=y+dir[1];

            //判断是否超出边界 tx<1||tx>n||ty<1||ty>m  下面这样写是因为n和m传不进来，硬传代码不优雅
            if(tx<1||tx>a.length-1||ty<1||ty>a[0].length-1){
                continue;
            }
            //判断是否是墙
            if(a[tx][ty]==2){
                continue;
            }
            //如果试探位置未被访问，且是空地
            if(a[tx][ty]==1&& !visited[tx][ty]){
                visited[tx][ty]=true;//设置已访问
                dfs1(tx,ty,step+1);
                visited[tx][ty]=false;
            }
        }
        return;//回退
    }
}