@toc

1、并查集的概念

并查集，在一些有N个元素的集合应用问题中，我们通常是在开始时让每个元素构成一个单元素的集合，然后按一定顺序将属于同一组的元素所在的集合合并，其间要反复查找一个元素在哪个集合中。这一类问题近几年来反复出现在信息学的国际国内赛题中。其特点是看似并不复杂，但数据量极大，若用正常的数据结构来描述的话，往往在空间上过大，计算机无法承受；即使在空间上勉强通过，运行的时间复杂度也极高，根本就不可能在比赛规定的运行时间（1～3秒）内计算出试题需要的结果，只能用并查集来描述。

此概念来源于百度百科

并查集是一种非常精巧的数据结构，它主要用于处理一些不相交集合的合并问题。一些常见的用途有求连通子图、求最小生成树的Kruskal算法和求最近公共祖先(LCA)等。

2、并查集的基本操作

2.1 初始化操作

假设有编号未1-n的n个元素，我们用一个数组fa[]来存储每个元素的父节点，刚开始的时候我们直接将它们的父节点指向自己就行。

private static int[] fa;
//1.初始化
public static void init(int n){
    fa=new int[n+1];
    //假设有编号未1-n的n个元素，我们用一个数组fa[]存储每个元素的父节点
    //开始的时候，我们先将它们的父节点设为自己
    for (int i = 1; i <=n ; i++) {
        fa[i]=i;
    }
}

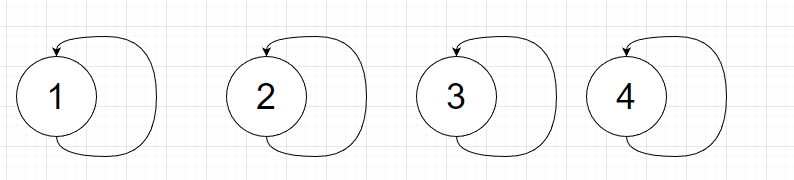
2.2 查询操作

查询操作：找到i的祖先直接返回，这里有两种，一种是未进行路径压缩的版本，这种容易超时，我们一般使用的都是经过路径压缩的代码。

未进行路径压缩的代码如下所示：

    public static int find(int i){
        if(fa[i]==i){   //递归出口，当打打了祖先位置，就返回祖先
           return i;
       }else{
           return find(fa[i]);//不断往上查找祖先
        }
    }

这种每次找某个数的祖先的时候都是一层一层往上递归，如果层数特别深就非常容易超时。

经过路径压缩之后的优化版本如下：

//2.查询：路径压缩版本
public static int find(int i){
    if(fa[i]==i){
        return i;
    }else{
        fa[i]=find(fa[i]);  //这一步进行了路径压缩
        return fa[i];   //返回父节点
    }
}

路径压缩前后的示意图如下所示：

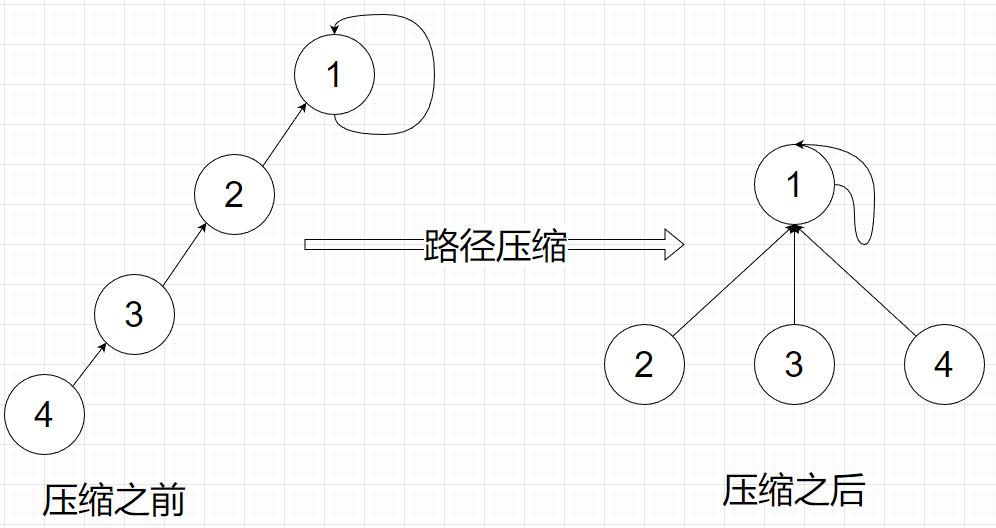
第二种查找祖先节点明显比第一种快多了

2.3 合并操作

我们对两个节点执行合并操作，输入为i和j，我们先找到i的祖先，再找到j的祖先，然后让i的祖先指向j的祖先(i和j的顺序换下也可以)。

public static void union(int i,int j){
    int i_father=find(i);//找到i的祖先
    int j_father=find(j);//找到j的祖先
    fa[i_father]=j_father;  //i的祖先指向j的祖先(i、j换下也可以)
}

3、并查集应用

3.1 蓝桥幼儿园

3.1.1 题目描述

蓝桥幼儿园的学生是如此的天真无邪，以至于对他们来说，朋友的朋友就是朋友。小明是蓝桥幼儿园的老师，这天他决定为学生们举办一个交友活动，活动规则如下:

小明会用红绳连接两名学生，被选中的两个学生将成为朋友。

小明想让所有学生都互相成为朋友，但是蓝桥幼儿园的学生是在太多了，他无法用肉眼判断某两个学生是否为朋友。于是他请来了作为编程大师的你，请你帮忙写程序判断某两个学生是否为朋友(默认自己和自己也是朋友)。

输入描述

第1行包含两个正整数N,M,其中N表示蓝桥幼儿园的学生数量，学生的编号分别为 $1 \sim N$。之后的第 $2\sim M+1$行每行输入三个整数，op,x,y:

• 如果op=1,表示小明用红绳连接了学生x和学生y。
• 如果op=2,请你回答小明学生x和学生y是否为朋友。

$1\le N,M\le 2\times 10^5,1\le x,y\le N。$

输出描述

对于每个op=2的输入，如果x和y是朋友，则输出一行YES，否则输出一行NO。

输出输出样例

输入

5 5
2 1 2
1 1 3
2 1 3
1 2 3
2 1 2

输出

NO
YES
YES

3.1.2 解题思路

• 这很明显可以使用并查集解决，我们用一个数组初始化这N个学生，刚开始的时候每个学生都和自己是朋友（每个节点的父亲都是它本身），也就是说他们fa[i]=i。
• 按照输入的顺序进行操作，如果输入的是op=1，则我们对x和y使用合并操作union(x,y),即将x的祖先指向y节点的祖先。
• 如果输入的是op=2，则我们使用find(x)和find(y)函数分别取查找x和y的祖先，若他们有共同的祖先，则说明这两个孩子是朋友，输出YES；否则输出NO。

3.1.3 代码实现

import java.util.Scanner;

public class Main {
    public static int[] fa;
    //初始化
    public static void init(int n){
        fa=new int[n+1];
        for (int i = 1; i <=n ; i++) {
            fa[i]=i;
        }
    }
    //查询:找到i的祖先直接返回
    public static int find(int i){
        if(fa[i]==i){
            return i;
        }else{
            fa[i]=find(fa[i]);
            return fa[i];
        }
    }

    //合并:让i的祖先指向j的祖先
    public static void union(int i,int j){
        int i_father = find(i);//找到i的祖先
        int j_father = find(j);//找到j的祖先
        fa[i_father]=j_father;  //让i的祖先指向j的祖先
    }

    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        //N个数
        int N = scan.nextInt();
        //M次操作
        int M = scan.nextInt();
        init(N);	//初始化
        for (int i = 0; i <M; i++) {
            int op = scan.nextInt();
            int x = scan.nextInt();
            int y = scan.nextInt();
            if(op==1){
                union(x,y);
            }else{
                if(find(x)==find(y)){
                    System.out.println("YES");
                }else{
                    System.out.println("NO");
                }
            }
        }
        scan.close();
    }
}

测试用例

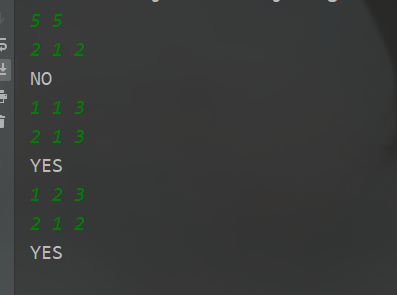
并查集基本操作参考链接：https://www.bilibili.com/video/BV1jv411a7LK/?vd_source=2ce79abf5d0d27bf7f3f2c38406c8eb6