01、训练流程

1●场景说明

通过员工工作年限与工资的对应关系表，找出二者之间的关系，并预测在指定的年限时，工资会有多少。

可以看出，这是一个用工作年限预测工资的简单线性回归问题。下面让按照最简单的流程来解决这个问题。

2●确定数据

观察数据是做数据分析等机器学习的第一步。这一步的主要目的是对训练数据有初步的认识。比如观察数据的特征含义，确定哪些特征是有效的，哪些特征是无效的，数据是否完整，有无缺失。

这一步能够帮助我们对数据有一个大致的理解。

员工的工资信息如表1所示，每一列代表数据的一个特征，分别是“姓名”、“年限”、“级别”、“工资”。

在这些特征中，“姓名”一般不会影响到工资收入，可以将“姓名”作为无效的特征，不纳入训练的数据当中。

因此这个数据集的特征向量即为{年限，级别，工资}。“工资”是结果，而“年限”和“级别”两个因素共同决定了“工资”。

“工资”之所以难以预测，是因为工资并不是根据某个固定的公式计算出来的，其中也包含了复杂的“人”的因素，比如员工的为人处世，老板是否赏识等等。

表1 年限和工资数据

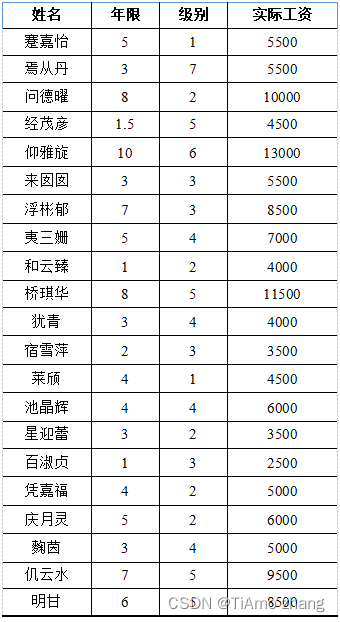
以上数据保存为csv表格文件，使用Python的pandas库读取以上数据的代码如下：

#工作年限、级别与工资数据(csv文件)csv_data= ‘salary.csv’
#读入dataframe
df = pandas.read_csv(StringIO(csv_data))
print(df)

3●确定模型

通过线性模型来预测一下年限和工资的关系。为了简单理解，首先考虑“年限”和“工资”两者之间的关系。

假定工资表示为y，年限表示为x，两者符合线性模型，那么这个模型就可以设为y=ax+b。使用二维坐标来显示年限和工资数据如图2所示，年限和工资基本呈现一个线性增长的形状。

使用Python的sklearn库建立模型的代码如下：

# 建立线性回归模型
regr = linear_model.LinearRegression()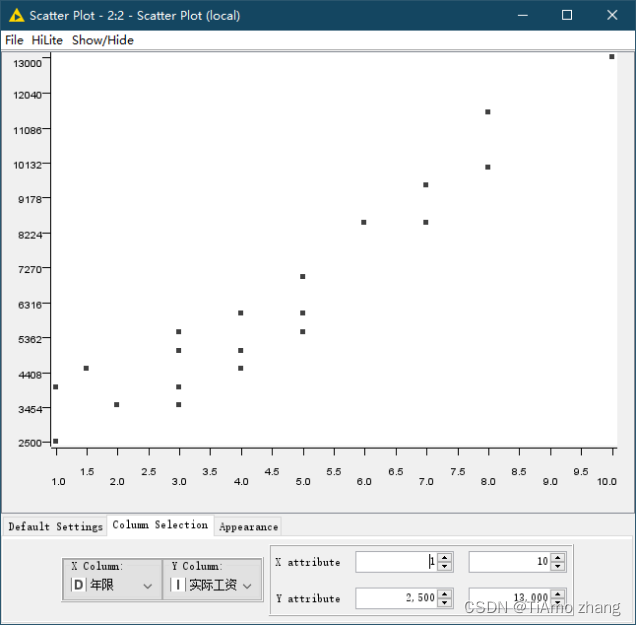

图2 工资年限数据样本

4●训练模型

在确定了模型之后，就可以使用现有的数据来训练模型。训练的过程实际上就是调整参数a、b的过程，这个过程叫做拟合。训练的目标就是确定y=ax+b，使这条直线最大限度地接近这些散点。

可以想象，如果员工的数据非常少，那么参数a和b计算的结果是不准确的，随着员工的数据增多，也就是训练集变大，参数a、b的计算结果将越来越精确。

当然，随着训练的次数不断增多，a、b的值会有一个精确的极限，当它们不能够再被精确时，则被认为这个模型已经训练的“足够”好了，这个结果叫做“收敛”。

如图3-16所示，一开始只用前三条数据来训练（图中红框标记的点），这时拟合的直线为a=947.3684，b=1947.3684（图中红色的直线）。

在图中可以直观地看出，红色的这条线并不能最大程度地贴合各个样本数据，认为在数据量少时，结果并不精确。当使用所有的22个数据进行训练时，生成的黑色直线明显要优于红色的直线。此时a=1083.073，b=1511.0797。

图中这条线就是线性回归的结果，其实际意义代表在已知的工作年限下，对应的高度就是预测的收入。不同迭代次数下的拟合结果如图3所示。

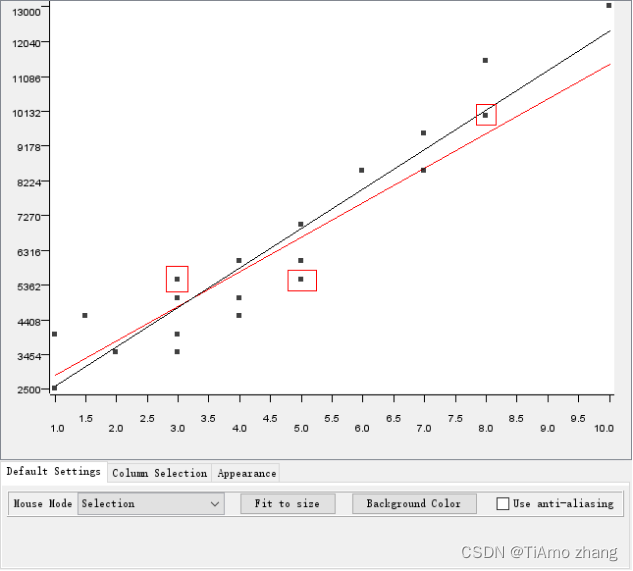
图3 不同迭代次数下的工资年限回归线

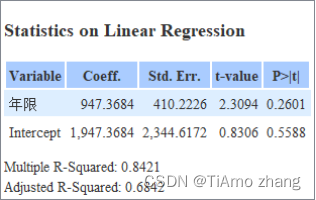
图4 不同迭代次数下的拟合结果

使用Python的sklearn库训练模型的代码如下：

# 填入数据并训练
regr.fit(df['年限'].reshape(-1, 1), df['实际工资']) # 注意此处.reshape(-1, 1)，因为X是一维的！
# 得到直线的斜率、截距
a, b = regr.coef_, regr.intercept_
print(a,b)

5●让预测更精确

通过上面的实验可以看到，实际预测的收入和真实收入总是有或大或小的差距，这条线只是代表了整体预测的误差最小的情况。那么使预测更加精确就是训练模型并进行调优的目标。

在上面的模型中，只使用了一个特征值{年限}。这种使用一个特征去拟合另一个特征的回归，称之为一元线性回归。在实际的数据中，还存在另一个特征“级别”，该特征也会对“收入”产生影响，因此应该将此特征也纳入训练的过程中，将特征向量的尺度由一元变为二元的{年限，级别}。

这种由多个特征去拟合另一个特征的回归，称之为多元线性回归，此时的模型就变为y=ax1+bx2+c。利用这个新的模型，重新训练数据并观察结果。

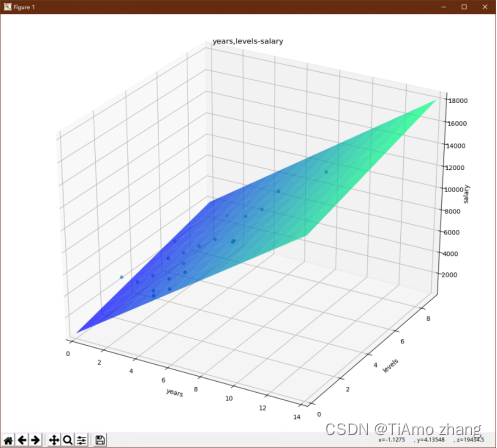
图5 二元拟合平面

从图5所示中可以看出，二维特征向量加上一个结果特征构成了三维空间中的点，而空间中的平面则是二元线性回归拟合的平面，平面上的任意一点就是该点对应的年限和级别时所预测的薪水。

从上面可以看出，随着线性回归特征向量尺度的增加，模型也会跟着变得复杂，而一般来说训练的结果也会变得更好。

一维特征向量拟合的是一条直线，二维特征向量拟合的是一个平面，那么三维、四维拟合成的会是一个什么东西？

对于高维向量，并不能用三维空间坐标表示出来，这个理论的高维平面称之为超平面。在实际很多应用中，对于事物的描述往往通过多个特征来描述，训练数据的特征向量也就基本都是高维特征向量了。

02、训练原理

模型通过训练，实现了比较准确的预测功能。下面内容将介绍一下模型是怎样训练才达到的这个结果。

在这里，大家不必过于担心，我们不会陷入数学的陷阱，只需要了解训练的原理就可以了。

想象一下，一个婴儿是怎样能够学会辨别猫还是狗呢？

首先，他必须接触大量猫和狗的图片，其次，每一次对猫或狗的辨认一定需要家长给予反馈。辨别错了，家长会表现的不开心，语气生硬；而辨别正确，家长则会表现的开心，并给予奖励。

正是在这样的反馈当中，婴儿的辨识能力不断加强。在机器学习中扮演这个家长角色的就是损失函数。损失函数是用来估量模型的预测值与真实值的不一致程度，它是一个非负实值函数。

损失函数越小，模型的稳健性就越好。

训练的过程就是模型通过不断的迭代调整各个参数，使得损失函数达到一个相对最小的状态。

1●梯度

接下来的问题是，怎样调整模型参数使得损失函数不断变小呢？

到了这个层面，问题其实更接近于数学编程问题，只需要理解方法即可。使得损失函数最小化的方法一般为梯度下降法。

可以把梯度想象为表示一个曲线或曲面上某一点的陡峭程度，如图6所示，分别在紫点和红点的地方做一条切线可以发现，两条切线的方向不同，切线的倾斜角度不同。

紫色点位置的切线斜率为负，称之为负梯度，红色点位置的切线斜率为正，称之为正梯度。这里的正负只表示为方向，并不表示大小，所以红色点出的梯度会更小一些。

有这样一个规律不难看出，如果人走在一条崎岖的道路上，先走下坡路，后来走上坡路，那么在这段路中间一定存在一个最低的点。即在梯度分别为正负的两个点之间，一定存在一个梯度为0的点。

如果模型的损失函数是一元的，那么就可以把模型参数和损失函数表示为图6中所示的样子，目标就是在这条曲线中找到最低的那个点，这个点就是损失函数的最小值点，一般认为此时模型达到了收敛。

图6 损失函数梯度曲线

同样，如果损失函数是二元的，就可以把模型参数和损失函数拟合为一个曲面。如图7所示，为珠穆朗玛峰的地形曲面，颜色越深表示地形越低，颜色越浅表示地形越高。因此颜色变化幅度大的地方，就是梯度大的地方，目标就是从这个曲面中找到最低的那个点。

图7 二元梯度曲面

2●梯度下降

在图7中的梯度曲线中，从紫色的点走到最低的那个点，可以利用下面公式：

下一个位置=当前位置-学习率×梯度

当初始位置在左侧时，往右走一段距离（学习率），看看当前位置是不是比原来的位置更低，如果是，就继续往右走；当下一步跨过最低点时就会发现，当前的位置没有更低反而升高时，这就说明走过了，需要反过来再往回走。这样不断的循环，最终就会找到最低点。

3●学习率

在上面的公式中可以看出，使用梯度下降法最重要的一个因素是学习率。

如图8所示，设置不同的学习率。

如果学习率定得太高，步子迈得太大，好处是可以走的很快，但会总是在最低点上跨来跨去，最终找到的最小值离实际的最小值误差会比较大；如果学习率定得太低，步子迈得太小，会更容易接近实际的最小值，但是速度会变慢、效率低。

如何设置学习率则考验机器学习的运用能力和经验。

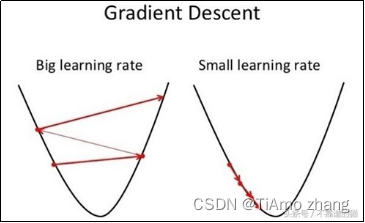
图8 不同的学习率

4●过拟合问题

再次回到工作年限与工资收入的关系这个问题，只用一条直线来拟合年限与工资的关系，如果使用一条曲线来拟合，这条曲线会更加贴合每一个样本数据，也就更加精确了，如图9所示。

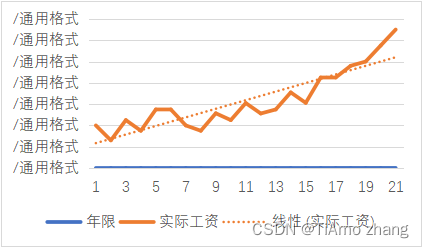
图9 一次多项式拟合曲线

y=ax+b属于一次多项式，把次数增加为二次多项式，模型就变为y=ax2+bx+c，此时拟合的预测线就由直线变为图10中的曲线。

图10 二次多项式拟合曲线

继续把模型变为三次多项式y=ax3+bx2+cx+d，此时预测线就变为图11中的曲线。

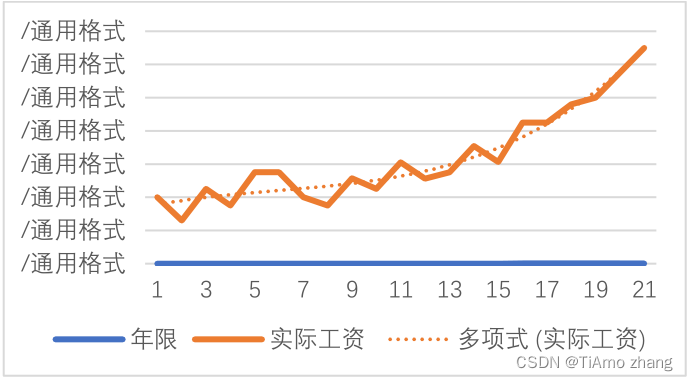
图11 三次多项式拟合曲线

以此类推，不断把模型变为4次5次6次，观察图12、图13、图14曲线在图中的变化情况。

图12 四次多项式拟合曲线

图13 五次多项式拟合曲线

图14 六次多项式拟合曲线

从图中可以看出，随着模型次数的增加，预测线会拟合得越来越好，越来越贴近实际的采样点，但这并不能说明模型越来越好。

因为现实中样本的特征数据并不是完全精确的，其中会有很多干扰因素，例如有的老板和某些员工更合拍，发的工资就会更高，这种情况下，年限这个因素相比就是次要因素。

在年限-工资这个模型中，模型拟合的越好，就代表模型把年限和工资建立起更强的联系，越把年限因素看成绝对因素，越会把一些特殊的，不符合规律的样本点过多的采纳。就像是学生学习学傻了，学成了书呆子，只会考试某种试题，稍微一变就不会了。

过拟合就是模型完美地或者很好地拟合了数据集中的有效数据，同时也很好的拟合了数据集中的错误数据，但是此模型很可能不能很好地用来预测数据集的其他部分。

如图15所示，如果拟合的曲线完全符合样本点，不难看出对于大部分位置的预测都是离谱的，这就属于严重的过拟合。

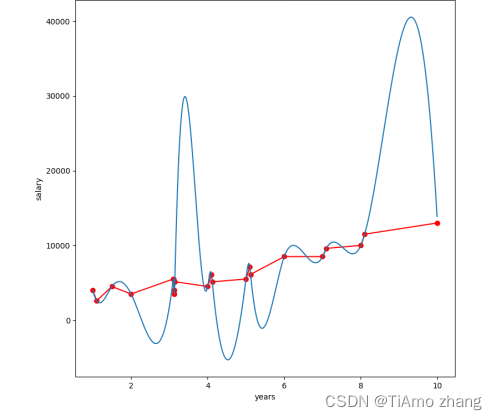
图15 过拟合的极端情况