工业蒸汽量预测（最新版本下篇）

5.模型验证

5.1模型评估的概念与正则化

5.1.1 过拟合与欠拟合

### 获取并绘制数据集
import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

np.random.seed(666)
x = np.random.uniform(-3.0, 3.0, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, size=100)

plt.scatter(x, y)
plt.show()

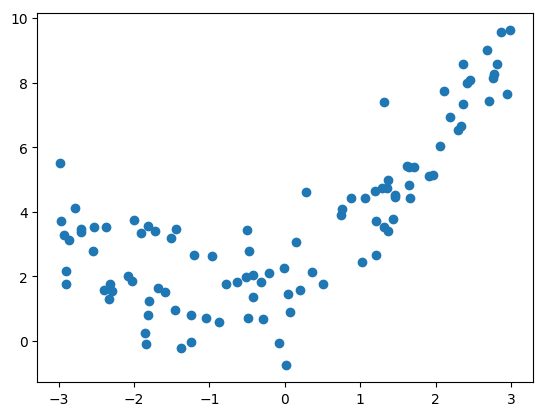
使用线性回归拟合数据

from sklearn.linear_model import LinearRegression

lin_reg = LinearRegression()
lin_reg.fit(X, y)
lin_reg.score(X, y)
# 输出：0.4953707811865009

0.4953707811865009

准确率为 0.495，比较低，直线拟合数据的程度较低。

### 使用均方误差判断拟合程度
from sklearn.metrics import mean_squared_error

y_predict = lin_reg.predict(X)
mean_squared_error(y, y_predict)
# 输出：3.0750025765636577

3.0750025765636577

### 绘制拟合结果
y_predict = lin_reg.predict(X)
plt.scatter(x, y)
plt.plot(np.sort(x), y_predict[np.argsort(x)], color='r')
plt.show()

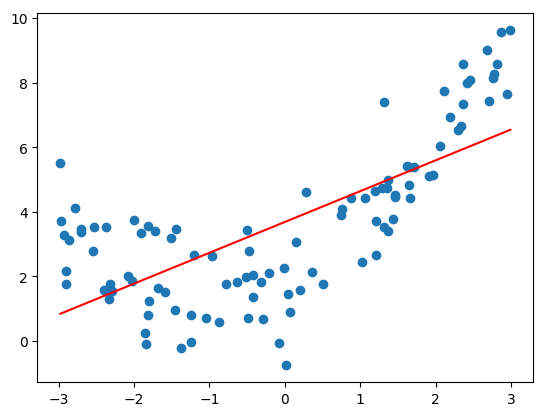
5.1.2 回归模型的评估指标和调用方法

### 使用多项式回归拟合
# * 封装 Pipeline 管道
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler

def PolynomialRegression(degree):
    return Pipeline([
        ('poly', PolynomialFeatures(degree=degree)),
        ('std_scaler', StandardScaler()),
        ('lin_reg', LinearRegression())
    ])

• 使用 Pipeline 拟合数据：degree = 2

poly2_reg = PolynomialRegression(degree=2)
poly2_reg.fit(X, y)

y2_predict = poly2_reg.predict(X)

# 比较真值和预测值的均方误差
mean_squared_error(y, y2_predict)
# 输出：1.0987392142417856

1.0987392142417856

• 绘制拟合结果

plt.scatter(x, y)
plt.plot(np.sort(x), y2_predict[np.argsort(x)], color='r')
plt.show()

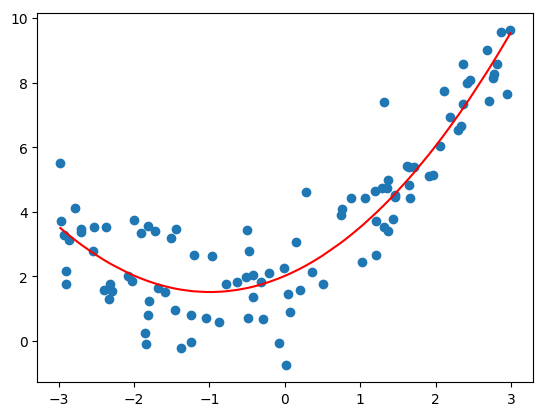
• 调整 degree = 10

poly10_reg = PolynomialRegression(degree=10)
poly10_reg.fit(X, y)

y10_predict = poly10_reg.predict(X)
mean_squared_error(y, y10_predict)
# 输出：1.0508466763764164


plt.scatter(x, y)
plt.plot(np.sort(x), y10_predict[np.argsort(x)], color='r')
plt.show()

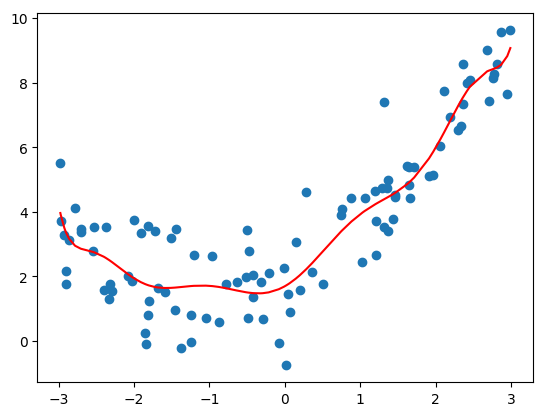
• 调整 degree = 100

poly100_reg = PolynomialRegression(degree=100)
poly100_reg.fit(X, y)

y100_predict = poly100_reg.predict(X)
mean_squared_error(y, y100_predict)
# 输出：0.6874357783433694


plt.scatter(x, y)
plt.plot(np.sort(x), y100_predict[np.argsort(x)], color='r')
plt.show()

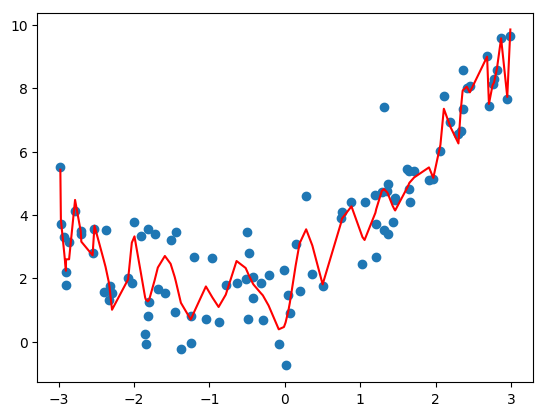
• 分析
  1. degree=2：均方误差为 1.0987392142417856；
  2. degree=10：均方误差为 1.0508466763764164；
  3. degree=100：均方误差为 0.6874357783433694；
  4. degree 越大拟合的效果越好，因为样本点是一定的，我们总能找到一条曲线将所有的样本点拟合，也就是说将所有的样本点都完全落在这根曲线上，使得整体的均方误差为 0；
  5. 红色曲线并不是所计算出的拟合曲线，而此红色曲线只是原有的数据点对应的 y 的预测值连接出来的结果，而且有的地方没有数据点，因此连接的结果和原来的曲线不一样；

5.1.3 交叉验证

• 交叉验证迭代器

K折交叉验证： KFold 将所有的样例划分为 k 个组，称为折叠 (fold) （如果 k = n， 这等价于 Leave One Out（留一） 策略），都具有相同的大小（如果可能）。预测函数学习时使用 k - 1 个折叠中的数据，最后一个剩下的折叠会用于测试。

K折重复多次： RepeatedKFold 重复 K-Fold n 次。当需要运行时可以使用它 KFold n 次，在每次重复中产生不同的分割。

留一交叉验证： LeaveOneOut (或 LOO) 是一个简单的交叉验证。每个学习集都是通过除了一个样本以外的所有样本创建的，测试集是被留下的样本。 因此，对于 n 个样本，我们有 n 个不同的训练集和 n 个不同的测试集。这种交叉验证程序不会浪费太多数据，因为只有一个样本是从训练集中删除掉的:

留P交叉验证： LeavePOut 与 LeaveOneOut 非常相似，因为它通过从整个集合中删除 p 个样本来创建所有可能的 训练/测试集。对于 n 个样本，这产生了 {n \choose p} 个 训练-测试 对。与 LeaveOneOut 和 KFold 不同，当 p > 1 时，测试集会重叠。

用户自定义数据集划分： ShuffleSplit 迭代器将会生成一个用户给定数量的独立的训练/测试数据划分。样例首先被打散然后划分为一对训练测试集合。

设置每次生成的随机数相同： 可以通过设定明确的 random_state ，使得伪随机生成器的结果可以重复。

• 基于类标签、具有分层的交叉验证迭代器

如何解决样本不平衡问题？ 使用StratifiedKFold和StratifiedShuffleSplit 分层抽样。 一些分类问题在目标类别的分布上可能表现出很大的不平衡性：例如，可能会出现比正样本多数倍的负样本。在这种情况下，建议采用如 StratifiedKFold 和 StratifiedShuffleSplit 中实现的分层抽样方法，确保相对的类别频率在每个训练和验证 折叠 中大致保留。

StratifiedKFold是 k-fold 的变种，会返回 stratified（分层） 的折叠：每个小集合中， 各个类别的样例比例大致和完整数据集中相同。

StratifiedShuffleSplit是 ShuffleSplit 的一个变种，会返回直接的划分，比如： 创建一个划分，但是划分中每个类的比例和完整数据集中的相同。

• 用于分组数据的交叉验证迭代器

如何进一步测试模型的泛化能力？ 留出一组特定的不属于测试集和训练集的数据。有时我们想知道在一组特定的 groups 上训练的模型是否能很好地适用于看不见的 group 。为了衡量这一点，我们需要确保验证对象中的所有样本来自配对训练折叠中完全没有表示的组。

GroupKFold是 k-fold 的变体，它确保同一个 group 在测试和训练集中都不被表示。 例如，如果数据是从不同的 subjects 获得的，每个 subject 有多个样本，并且如果模型足够灵活以高度人物指定的特征中学习，则可能无法推广到新的 subject 。 GroupKFold 可以检测到这种过拟合的情况。

LeaveOneGroupOut是一个交叉验证方案，它根据第三方提供的 array of integer groups （整数组的数组）来提供样本。这个组信息可以用来编码任意域特定的预定义交叉验证折叠。

每个训练集都是由除特定组别以外的所有样本构成的。

LeavePGroupsOut类似于 LeaveOneGroupOut ，但为每个训练/测试集删除与 P 组有关的样本。

GroupShuffleSplit迭代器是 ShuffleSplit 和 LeavePGroupsOut 的组合，它生成一个随机划分分区的序列，其中为每个分组提供了一个组子集。

• 时间序列分割

TimeSeriesSplit是 k-fold 的一个变体，它首先返回 k 折作为训练数据集，并且 (k+1) 折作为测试数据集。 请注意，与标准的交叉验证方法不同，连续的训练集是超越前者的超集。 另外，它将所有的剩余数据添加到第一个训练分区，它总是用来训练模型。

5.2 网格搜索

Grid Search：一种调参手段；穷举搜索：在所有候选的参数选择中，通过循环遍历，尝试每一种可能性，表现最好的参数就是最终的结果。其原理就像是在数组里找最大值。

5.2.1 简单的网格搜索

from sklearn.datasets import load_iris
from sklearn.svm import SVC
from sklearn.model_selection import train_test_split

iris = load_iris()
X_train,X_test,y_train,y_test = train_test_split(iris.data,iris.target,random_state=0)
print("Size of training set:{} size of testing set:{}".format(X_train.shape[0],X_test.shape[0]))

####   grid search start
best_score = 0
for gamma in [0.001,0.01,0.1,1,10,100]:
    for C in [0.001,0.01,0.1,1,10,100]:
        svm = SVC(gamma=gamma,C=C)#对于每种参数可能的组合，进行一次训练；
        svm.fit(X_train,y_train)
        score = svm.score(X_test,y_test)
        if score > best_score:#找到表现最好的参数
            best_score = score
            best_parameters = {'gamma':gamma,'C':C}
####   grid search end

print("Best score:{:.2f}".format(best_score))
print("Best parameters:{}".format(best_parameters))

Size of training set:112 size of testing set:38
Best score:0.97
Best parameters:{'gamma': 0.001, 'C': 100}

5.2.2 Grid Search with Cross Validation（具有交叉验证的网格搜索）

交叉验证经常与网格搜索进行结合，作为参数评价的一种方法，这种方法叫做grid search with cross validation。sklearn因此设计了一个这样的类GridSearchCV，这个类实现了fit，predict，score等方法，被当做了一个estimator，使用fit方法，该过程中：（1）搜索到最佳参数；（2）实例化了一个最佳参数的estimator；

from sklearn.model_selection import GridSearchCV

#把要调整的参数以及其候选值 列出来；
param_grid = {"gamma":[0.001,0.01,0.1,1,10,100],
             "C":[0.001,0.01,0.1,1,10,100]}
print("Parameters:{}".format(param_grid))

grid_search = GridSearchCV(SVC(),param_grid,cv=5) #实例化一个GridSearchCV类
X_train,X_test,y_train,y_test = train_test_split(iris.data,iris.target,random_state=10)
grid_search.fit(X_train,y_train) #训练，找到最优的参数，同时使用最优的参数实例化一个新的SVC estimator。
print("Test set score:{:.2f}".format(grid_search.score(X_test,y_test)))
print("Best parameters:{}".format(grid_search.best_params_))
print("Best score on train set:{:.2f}".format(grid_search.best_score_))

Parameters:{'gamma': [0.001, 0.01, 0.1, 1, 10, 100], 'C': [0.001, 0.01, 0.1, 1, 10, 100]}
Test set score:0.97
Best parameters:{'C': 10, 'gamma': 0.1}
Best score on train set:0.98

5.2.3 学习曲线

digits = load_digits()
X, y = digits.data, digits.target


title = "Learning Curves (Naive Bayes)"
# Cross validation with 100 iterations to get smoother mean test and train
# score curves, each time with 20% data randomly selected as a validation set.
cv = ShuffleSplit(n_splits=100, test_size=0.2, random_state=0)

estimator = GaussianNB()
plot_learning_curve(estimator, title, X, y, ylim=(0.7, 1.01), cv=cv, n_jobs=4)

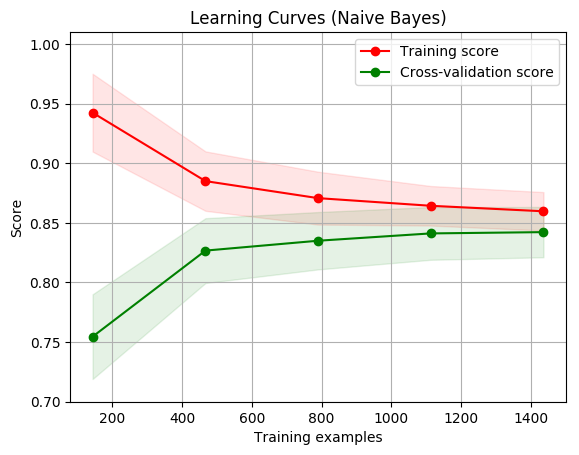
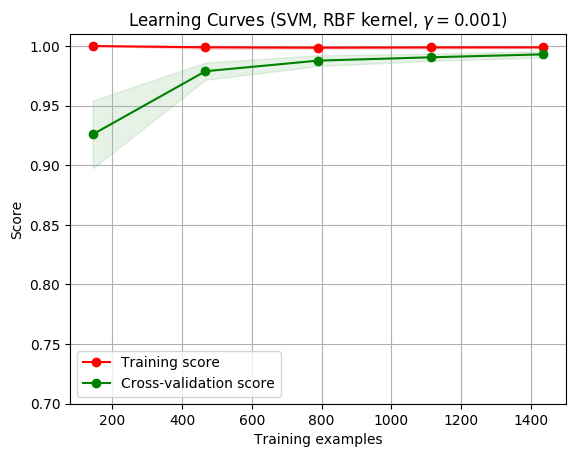
title = "Learning Curves (SVM, RBF kernel, $\gamma=0.001$)"
# SVC is more expensive so we do a lower number of CV iterations:
cv = ShuffleSplit(n_splits=10, test_size=0.2, random_state=0)
estimator = SVC(gamma=0.001)
plot_learning_curve(estimator, title, X, y, (0.7, 1.01), cv=cv, n_jobs=4)

<module 'matplotlib.pyplot' from '/opt/conda/envs/python35-paddle120-env/lib/python3.7/site-packages/matplotlib/pyplot.py'>

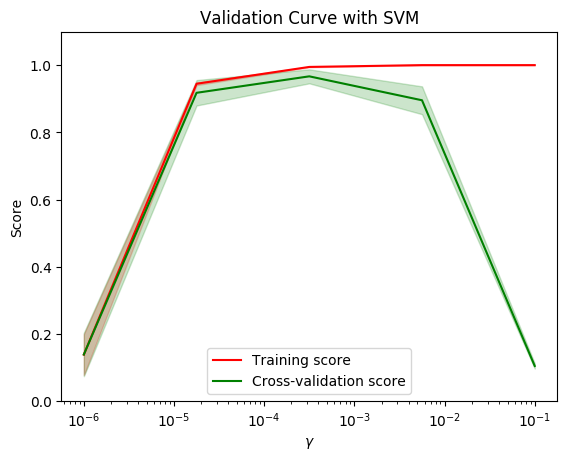
5.2.4 验证曲线

import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import load_digits
from sklearn.svm import SVC
from sklearn. model_selection import validation_curve

digits = load_digits()
X, y = digits.data, digits.target

param_range = np.logspace(-6, -1, 5)
train_scores, test_scores = validation_curve(
    SVC(), X, y, param_name="gamma", param_range=param_range,
    cv=10, scoring="accuracy", n_jobs=1)
train_scores_mean = np.mean(train_scores, axis=1)
train_scores_std = np.std(train_scores, axis=1)
test_scores_mean = np.mean(test_scores, axis=1)
test_scores_std = np.std(test_scores, axis=1)

plt.title("Validation Curve with SVM")
plt.xlabel("$\gamma$")
plt.ylabel("Score")
plt.ylim(0.0, 1.1)
plt.semilogx(param_range, train_scores_mean, label="Training score", color="r")
plt.fill_between(param_range, train_scores_mean - train_scores_std,
                 train_scores_mean + train_scores_std, alpha=0.2, color="r")
plt.semilogx(param_range, test_scores_mean, label="Cross-validation score",
             color="g")
plt.fill_between(param_range, test_scores_mean - test_scores_std,
                 test_scores_mean + test_scores_std, alpha=0.2, color="g")
plt.legend(loc="best")
plt.show()

5.3 工业蒸汽赛题模型验证

5.3.1 模型过拟合与欠拟合

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns

from scipy import stats

import warnings
warnings.filterwarnings("ignore")

from sklearn.linear_model import LinearRegression  #线性回归
from sklearn.neighbors import KNeighborsRegressor  #K近邻回归
from sklearn.tree import DecisionTreeRegressor     #决策树回归
from sklearn.ensemble import RandomForestRegressor #随机森林回归
from sklearn.svm import SVR  #支持向量回归
import lightgbm as lgb #lightGbm模型

from sklearn.model_selection import train_test_split # 切分数据
from sklearn.metrics import mean_squared_error #评价指标

from sklearn.linear_model import SGDRegressor

# 下载需要用到的数据集
!wget http://tianchi-media.oss-cn-beijing.aliyuncs.com/DSW/Industrial_Steam_Forecast/zhengqi_test.txt
!wget http://tianchi-media.oss-cn-beijing.aliyuncs.com/DSW/Industrial_Steam_Forecast/zhengqi_train.txt

train_data_file = "./zhengqi_train.txt"
test_data_file =  "./zhengqi_test.txt"

train_data = pd.read_csv(train_data_file, sep='\t', encoding='utf-8')
test_data = pd.read_csv(test_data_file, sep='\t', encoding='utf-8')

from sklearn import preprocessing 

features_columns = [col for col in train_data.columns if col not in ['target']]

min_max_scaler = preprocessing.MinMaxScaler()

min_max_scaler = min_max_scaler.fit(train_data[features_columns])

train_data_scaler = min_max_scaler.transform(train_data[features_columns])
test_data_scaler = min_max_scaler.transform(test_data[features_columns])

train_data_scaler = pd.DataFrame(train_data_scaler)
train_data_scaler.columns = features_columns

test_data_scaler = pd.DataFrame(test_data_scaler)
test_data_scaler.columns = features_columns

train_data_scaler['target'] = train_data['target']

from sklearn.decomposition import PCA   #主成分分析法

#PCA方法降维
#保留16个主成分
pca = PCA(n_components=16)
new_train_pca_16 = pca.fit_transform(train_data_scaler.iloc[:,0:-1])
new_test_pca_16 = pca.transform(test_data_scaler)
new_train_pca_16 = pd.DataFrame(new_train_pca_16)
new_test_pca_16 = pd.DataFrame(new_test_pca_16)
new_train_pca_16['target'] = train_data_scaler['target']

#采用 pca 保留16维特征的数据
new_train_pca_16 = new_train_pca_16.fillna(0)
train = new_train_pca_16[new_test_pca_16.columns]
target = new_train_pca_16['target']

# 切分数据 训练数据80% 验证数据20%
train_data,test_data,train_target,test_target=train_test_split(train,target,test_size=0.2,random_state=0)

#### 欠拟合
clf = SGDRegressor(max_iter=500, tol=1e-2) 
clf.fit(train_data, train_target)
score_train = mean_squared_error(train_target, clf.predict(train_data))
score_test = mean_squared_error(test_target, clf.predict(test_data))
print("SGDRegressor train MSE:   ", score_train)
print("SGDRegressor test MSE:   ", score_test)

SGDRegressor train MSE:    0.15125847407064866
SGDRegressor test MSE:    0.15565698772176442

### 过拟合
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(5)
train_data_poly = poly.fit_transform(train_data)
test_data_poly = poly.transform(test_data)
clf = SGDRegressor(max_iter=1000, tol=1e-3) 
clf.fit(train_data_poly, train_target)
score_train = mean_squared_error(train_target, clf.predict(train_data_poly))
score_test = mean_squared_error(test_target, clf.predict(test_data_poly))
print("SGDRegressor train MSE:   ", score_train)
print("SGDRegressor test MSE:   ", score_test)

SGDRegressor train MSE:    0.13230725829556678
SGDRegressor test MSE:    0.14475818228220433

### 正常拟合
from sklearn.preprocessing import PolynomialFeatures
poly = PolynomialFeatures(3)
train_data_poly = poly.fit_transform(train_data)
test_data_poly = poly.transform(test_data)
clf = SGDRegressor(max_iter=1000, tol=1e-3) 
clf.fit(train_data_poly, train_target)
score_train = mean_squared_error(train_target, clf.predict(train_data_poly))
score_test = mean_squared_error(test_target, clf.predict(test_data_poly))
print("SGDRegressor train MSE:   ", score_train)
print("SGDRegressor test MSE:   ", score_test)

SGDRegressor train MSE:    0.13399656558429307
SGDRegressor test MSE:    0.14255473176638828

5.3.2 模型正则化

L2范数正则化

poly = PolynomialFeatures(3)
train_data_poly = poly.fit_transform(train_data)
test_data_poly = poly.transform(test_data)
clf = SGDRegressor(max_iter=1000, tol=1e-3, penalty= 'L2', alpha=0.0001) 
clf.fit(train_data_poly, train_target)
score_train = mean_squared_error(train_target, clf.predict(train_data_poly))
score_test = mean_squared_error(test_target, clf.predict(test_data_poly))
print("SGDRegressor train MSE:   ", score_train)
print("SGDRegressor test MSE:   ", score_test)

SGDRegressor train MSE:    0.1344679787727263
SGDRegressor test MSE:    0.14283084627234435

L1范数正则化

poly = PolynomialFeatures(3)
train_data_poly = poly.fit_transform(train_data)
test_data_poly = poly.transform(test_data)
clf = SGDRegressor(max_iter=1000, tol=1e-3, penalty= 'L1', alpha=0.00001) 
clf.fit(train_data_poly, train_target)
score_train = mean_squared_error(train_target, clf.predict(train_data_poly))
score_test = mean_squared_error(test_target, clf.predict(test_data_poly))
print("SGDRegressor train MSE:   ", score_train)
print("SGDRegressor test MSE:   ", score_test)

SGDRegressor train MSE:    0.13516056789895906
SGDRegressor test MSE:    0.14330444056183564

ElasticNet L1和L2范数加权正则化

poly = PolynomialFeatures(3)
train_data_poly = poly.fit_transform(train_data)
test_data_poly = poly.transform(test_data)
clf = SGDRegressor(max_iter=1000, tol=1e-3, penalty= 'elasticnet', l1_ratio=0.9, alpha=0.00001) 
clf.fit(train_data_poly, train_target)
score_train = mean_squared_error(train_target, clf.predict(train_data_poly))
score_test = mean_squared_error(test_target, clf.predict(test_data_poly))
print("SGDRegressor train MSE:   ", score_train)
print("SGDRegressor test MSE:   ", score_test)

SGDRegressor train MSE:    0.13409834594770004
SGDRegressor test MSE:    0.14238154901534278

5.3.3 模型交叉验证

简单交叉验证 Hold-out-menthod

# 简单交叉验证
from sklearn.model_selection import train_test_split # 切分数据
# 切分数据 训练数据80% 验证数据20%
train_data,test_data,train_target,test_target=train_test_split(train,target,test_size=0.2,random_state=0)

clf = SGDRegressor(max_iter=1000, tol=1e-3) 
clf.fit(train_data, train_target)
score_train = mean_squared_error(train_target, clf.predict(train_data))
score_test = mean_squared_error(test_target, clf.predict(test_data))
print("SGDRegressor train MSE:   ", score_train)
print("SGDRegressor test MSE:   ", score_test)

SGDRegressor train MSE:    0.14143759510386256
SGDRegressor test MSE:    0.14691862910491496

K折交叉验证 K-fold CV

# 5折交叉验证
from sklearn.model_selection import KFold

kf = KFold(n_splits=5)
for k, (train_index, test_index) in enumerate(kf.split(train)):
    train_data,test_data,train_target,test_target = train.values[train_index],train.values[test_index],target[train_index],target[test_index]
    clf = SGDRegressor(max_iter=1000, tol=1e-3) 
    clf.fit(train_data, train_target)
    score_train = mean_squared_error(train_target, clf.predict(train_data))
    score_test = mean_squared_error(test_target, clf.predict(test_data))
    print(k, " 折", "SGDRegressor train MSE:   ", score_train)
    print(k, " 折", "SGDRegressor test MSE:   ", score_test, '\n')  

4  折 SGDRegressor train MSE:    0.13809527090941803
4  折 SGDRegressor test MSE:    0.16535259610698216 

留一法 LOO CV

from sklearn.model_selection import LeaveOneOut
loo = LeaveOneOut()
num = 100
for k, (train_index, test_index) in enumerate(loo.split(train)):
    train_data,test_data,train_target,test_target = train.values[train_index],train.values[test_index],target[train_index],target[test_index]
    clf = SGDRegressor(max_iter=1000, tol=1e-3) 
    clf.fit(train_data, train_target)
    score_train = mean_squared_error(train_target, clf.predict(train_data))
    score_test = mean_squared_error(test_target, clf.predict(test_data))
    print(k, " 个", "SGDRegressor train MSE:   ", score_train)
    print(k, " 个", "SGDRegressor test MSE:   ", score_test, '\n') 
    if k >= 9:
        break

9  个 SGDRegressor train MSE:    0.1416518678123776
9  个 SGDRegressor test MSE:    0.049938663947863705 

留P法 LPO CV

from sklearn.model_selection import LeavePOut
lpo = LeavePOut(p=10)
num = 100
for k, (train_index, test_index) in enumerate(lpo.split(train)):
    train_data,test_data,train_target,test_target = train.values[train_index],train.values[test_index],target[train_index],target[test_index]
    clf = SGDRegressor(max_iter=1000, tol=1e-3) 
    clf.fit(train_data, train_target)
    score_train = mean_squared_error(train_target, clf.predict(train_data))
    score_test = mean_squared_error(test_target, clf.predict(test_data))
    print(k, " 10个", "SGDRegressor train MSE:   ", score_train)
    print(k, " 10个", "SGDRegressor test MSE:   ", score_test, '\n') 
    if k >= 9:
        break

9  10个 SGDRegressor train MSE:    0.14188082336683486
9  10个 SGDRegressor test MSE:    0.045133396081342994 

5.3.4 模型超参空间及调参

穷举网格搜索

from sklearn.model_selection import GridSearchCV
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split # 切分数据
# 切分数据 训练数据80% 验证数据20%
train_data,test_data,train_target,test_target=train_test_split(train,target,test_size=0.2,random_state=0)

randomForestRegressor = RandomForestRegressor()
parameters = {
              'n_estimators':[50, 100, 200],
              'max_depth':[1, 2, 3]
        }


clf = GridSearchCV(randomForestRegressor, parameters, cv=5)
clf.fit(train_data, train_target)

score_test = mean_squared_error(test_target, clf.predict(test_data))

print("RandomForestRegressor GridSearchCV test MSE:   ", score_test)
sorted(clf.cv_results_.keys())

RandomForestRegressor GridSearchCV test MSE:    0.2595696984416692

随机参数优化

from sklearn.model_selection import RandomizedSearchCV
from sklearn.ensemble import RandomForestRegressor
from sklearn.model_selection import train_test_split # 切分数据
# 切分数据 训练数据80% 验证数据20%
train_data,test_data,train_target,test_target=train_test_split(train,target,test_size=0.2,random_state=0)

randomForestRegressor = RandomForestRegressor()
parameters = {
              'n_estimators':[10, 50],
              'max_depth':[1, 2, 5]
        }


clf = RandomizedSearchCV(randomForestRegressor, parameters, cv=5)
clf.fit(train_data, train_target)

score_test = mean_squared_error(test_target, clf.predict(test_data))

print("RandomForestRegressor RandomizedSearchCV test MSE:   ", score_test)
sorted(clf.cv_results_.keys())

RandomForestRegressor RandomizedSearchCV test MSE:    0.1952974248358807

Lgb 调参

!pip install lightgbm

clf = lgb.LGBMRegressor(num_leaves=21)#num_leaves=31

parameters = {
    'learning_rate': [0.01, 0.1],
    'n_estimators': [20, 40]
}

clf = GridSearchCV(clf, parameters, cv=5)
clf.fit(train_data, train_target)

print('Best parameters found by grid search are:', clf.best_params_)
score_test = mean_squared_error(test_target, clf.predict(test_data))
print("LGBMRegressor RandomizedSearchCV test MSE:   ", score_test)

Lgb 线下验证

5.3.5 学习曲线和验证曲线

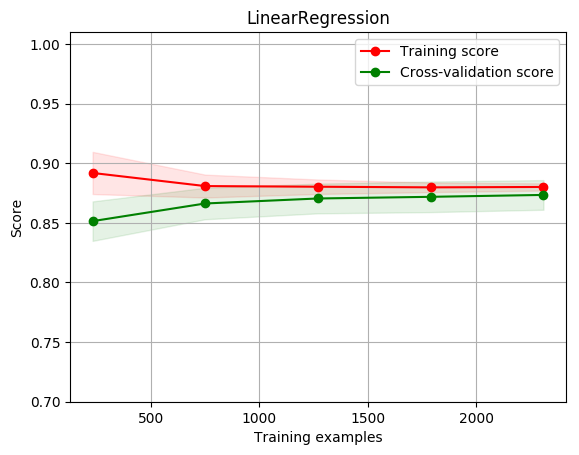
TypeError：__init __()为参数’n_splits’获得了多个值

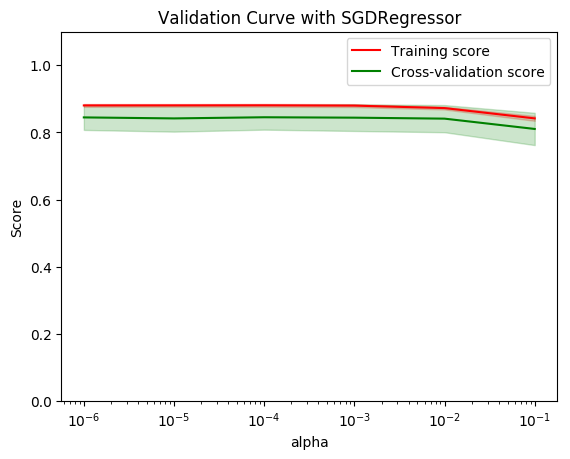
6.特征优化

6.1 定义特征构造方法，构造特征

6.2 基于lightgbm对构造特征进行训练和评估

# ls_validation i
from sklearn.model_selection import KFold

from sklearn.metrics import mean_squared_error
import lightgbm as lgb
import numpy as np

# 5折交叉验证，版本迭代参数更新
Folds=5
kf = KFold(n_splits=Folds, shuffle=True, random_state=2019)


# 版本修改导致用法有不同：
# 1. n_folds参数修改为n_splits
# 2. train_data.shape[0]参数被去除。所以你的这一行修改为kf =KFold(n_splits=3, random_state=1)
# 然后在你后面要用到kf的地方，比如原来的：
# for i, (train_index, test_index) in enumerate(kf):
# 修改成：
# for i, (train_index, test_index) in enumerate(kf.split(train)):# train就是你的训练数据

7.模型融合

对特征进行Box-Cox变换，使其满足正态性

Box-Cox变换是Box和Cox在1964年提出的一种广义幂变换方法，是统计建模中常用的一种数据变换，用于连续的响应变量不满足正态分布的情况。Box-Cox变换之后，可以一定程度上减小不可观测的误差和预测变量的相关性。Box-Cox变换的主要特点是引入一个参数，通过数据本身估计该参数进而确定应采取的数据变换形式，Box-Cox变换可以明显地改善数据的正态性、对称性和方差相等性，对许多实际数据都是行之有效的

7.1 单一模型预测效果

7.1.1 岭回归

model = 'Ridge'

opt_models[model] = Ridge()
alph_range = np.arange(0.25,6,0.25)
param_grid = {'alpha': alph_range}

opt_models[model],cv_score,grid_results = train_model(opt_models[model], param_grid=param_grid, 
                                              splits=splits, repeats=repeats)

cv_score.name = model
score_models = score_models.append(cv_score)

plt.figure()
plt.errorbar(alph_range, abs(grid_results['mean_test_score']),
             abs(grid_results['std_test_score'])/np.sqrt(splits*repeats))
plt.xlabel('alpha')
plt.ylabel('score')

7.1.2 Lasso回归

model = 'Lasso'

opt_models[model] = Lasso()
alph_range = np.arange(1e-4,1e-3,4e-5)
param_grid = {'alpha': alph_range}

opt_models[model], cv_score, grid_results = train_model(opt_models[model], param_grid=param_grid, 
                                              splits=splits, repeats=repeats)

cv_score.name = model
score_models = score_models.append(cv_score)

plt.figure()
plt.errorbar(alph_range, abs(grid_results['mean_test_score']),abs(grid_results['std_test_score'])/np.sqrt(splits*repeats))
plt.xlabel('alpha')
plt.ylabel('score')

7.1.3 ElasticNet 回归

model ='ElasticNet'
opt_models[model] = ElasticNet()

param_grid = {'alpha': np.arange(1e-4,1e-3,1e-4),
              'l1_ratio': np.arange(0.1,1.0,0.1),
              'max_iter':[100000]}

opt_models[model], cv_score, grid_results = train_model(opt_models[model], param_grid=param_grid, 
                                              splits=splits, repeats=1)

cv_score.name = model
score_models = score_models.append(cv_score)

7.1.4 SVR回归

model='LinearSVR'
opt_models[model] = LinearSVR()

crange = np.arange(0.1,1.0,0.1)
param_grid = {'C':crange,
             'max_iter':[1000]}

opt_models[model], cv_score, grid_results = train_model(opt_models[model], param_grid=param_grid, 
                                              splits=splits, repeats=repeats)


cv_score.name = model
score_models = score_models.append(cv_score)

plt.figure()
plt.errorbar(crange, abs(grid_results['mean_test_score']),abs(grid_results['std_test_score'])/np.sqrt(splits*repeats))
plt.xlabel('C')
plt.ylabel('score')

7.1.5 KNN最近邻

model = 'KNeighbors'
opt_models[model] = KNeighborsRegressor()

param_grid = {'n_neighbors':np.arange(3,11,1)}

opt_models[model], cv_score, grid_results = train_model(opt_models[model], param_grid=param_grid, 
                                              splits=splits, repeats=1)

cv_score.name = model
score_models = score_models.append(cv_score)

plt.figure()
plt.errorbar(np.arange(3,11,1), abs(grid_results['mean_test_score']),abs(grid_results['std_test_score'])/np.sqrt(splits*1))
plt.xlabel('n_neighbors')
plt.ylabel('score')

7.1.6 GBDT 模型

model = 'GradientBoosting'
opt_models[model] = GradientBoostingRegressor()

param_grid = {'n_estimators':[150,250,350],
              'max_depth':[1,2,3],
              'min_samples_split':[5,6,7]}

opt_models[model], cv_score, grid_results = train_model(opt_models[model], param_grid=param_grid, 
                                              splits=splits, repeats=1)

cv_score.name = model
score_models = score_models.append(cv_score)

7.1.7XGB模型

model = 'XGB'
opt_models[model] = XGBRegressor()

param_grid = {'n_estimators':[100,200,300,400,500],
              'max_depth':[1,2,3],
             }

opt_models[model], cv_score,grid_results = train_model(opt_models[model], param_grid=param_grid, 
                                              splits=splits, repeats=1)

cv_score.name = model
score_models = score_models.append(cv_score)

7.1.8 随机森林模型

model = 'RandomForest'
opt_models[model] = RandomForestRegressor()

param_grid = {'n_estimators':[100,150,200],
              'max_features':[8,12,16,20,24],
              'min_samples_split':[2,4,6]}

opt_models[model], cv_score, grid_results = train_model(opt_models[model], param_grid=param_grid, 
                                              splits=5, repeats=1)

cv_score.name = model
score_models = score_models.append(cv_score)

7.2 模型预测–多模型Bagging

def model_predict(test_data,test_y=[],stack=False):
    #poly_trans=PolynomialFeatures(degree=2)
    #test_data1=poly_trans.fit_transform(test_data)
    #test_data=MinMaxScaler().fit_transform(test_data)
    i=0
    y_predict_total=np.zeros((test_data.shape[0],))
    for model in opt_models.keys():
        if model!="LinearSVR" and model!="KNeighbors":
            y_predict=opt_models[model].predict(test_data)
            y_predict_total+=y_predict
            i+=1
        if len(test_y)>0:
            print("{}_mse:".format(model),mean_squared_error(y_predict,test_y))
    y_predict_mean=np.round(y_predict_total/i,3)
    if len(test_y)>0:
        print("mean_mse:",mean_squared_error(y_predict_mean,test_y))
    else:
        y_predict_mean=pd.Series(y_predict_mean)
        return y_predict_mean

# Bagging预测
model_predict(X_valid,y_valid)

7.3 模型融合Stacking

7.3.1 模型融合stacking简单示例

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.gridspec as gridspec
import itertools
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.ensemble import RandomForestClassifier

##主要使用pip install mlxtend安装mlxtend
from mlxtend.classifier import EnsembleVoteClassifier
from mlxtend.data import iris_data
from mlxtend.plotting import plot_decision_regions
%matplotlib inline

# Initializing Classifiers
clf1 = LogisticRegression(random_state=0)
clf2 = RandomForestClassifier(random_state=0)
clf3 = SVC(random_state=0, probability=True)
eclf = EnsembleVoteClassifier(clfs=[clf1, clf2, clf3], weights=[2, 1, 1], voting='soft')

# Loading some example data
X, y = iris_data()
X = X[:,[0, 2]]

# Plotting Decision Regions
gs = gridspec.GridSpec(2, 2)
fig = plt.figure(figsize=(10, 8))

for clf, lab, grd in zip([clf1, clf2, clf3, eclf],
                         ['Logistic Regression', 'Random Forest', 'RBF kernel SVM', 'Ensemble'],
                         itertools.product([0, 1], repeat=2)):
    clf.fit(X, y)
    ax = plt.subplot(gs[grd[0], grd[1]])
    fig = plot_decision_regions(X=X, y=y, clf=clf, legend=2)
    plt.title(lab)
plt.show()

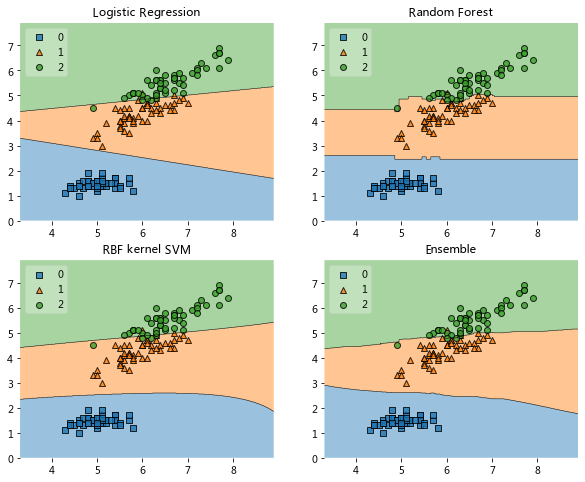
工业蒸汽多模型融合stacking

模型融合stacking基学习器

模型融合stacking预测

8.总结

本项目主要讲解了数据探索性分析：查看变量间相关性以及找出关键变量；数据特征工程对数据精进：异常值处理、归一化处理以及特征降维；在进行归回模型训练涉及主流ML模型：决策树、随机森林，lightgbm等；在模型验证方面：讲解了相关评估指标以及交叉验证等；同时用lgb对特征进行优化；最后进行基于stacking方式模型融合。

原项目链接：https://www.heywhale.com/home/column/64141d6b1c8c8b518ba97dcc

参考链接：https://tianchi.aliyun.com/course/278/3427