数据结构之二叉树的结构和遍历的实现
数据结构之二叉树的结构和遍历的实现
1.二叉树的存储结构
二叉树一般分为两种存储结构,一种是顺序结构,一种是链表结构。
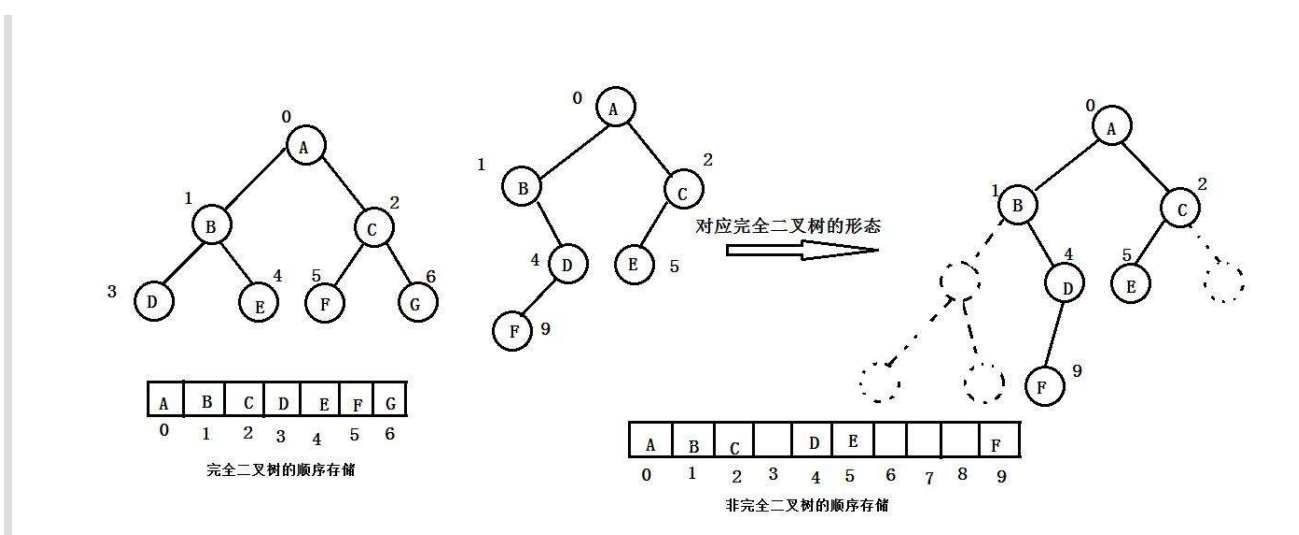
顺序结构
顺序结构存储就是使用数组来存储,一般使用数组只适合表示完全二叉树,因为不是完全二叉树会有空 间的浪费。而现实中使用中只有堆才会使用数组来存储。==二叉树顺 序存储在物理上是一个数组,在逻辑上是一颗二叉树==。(非完全二叉树很浪费空间!)
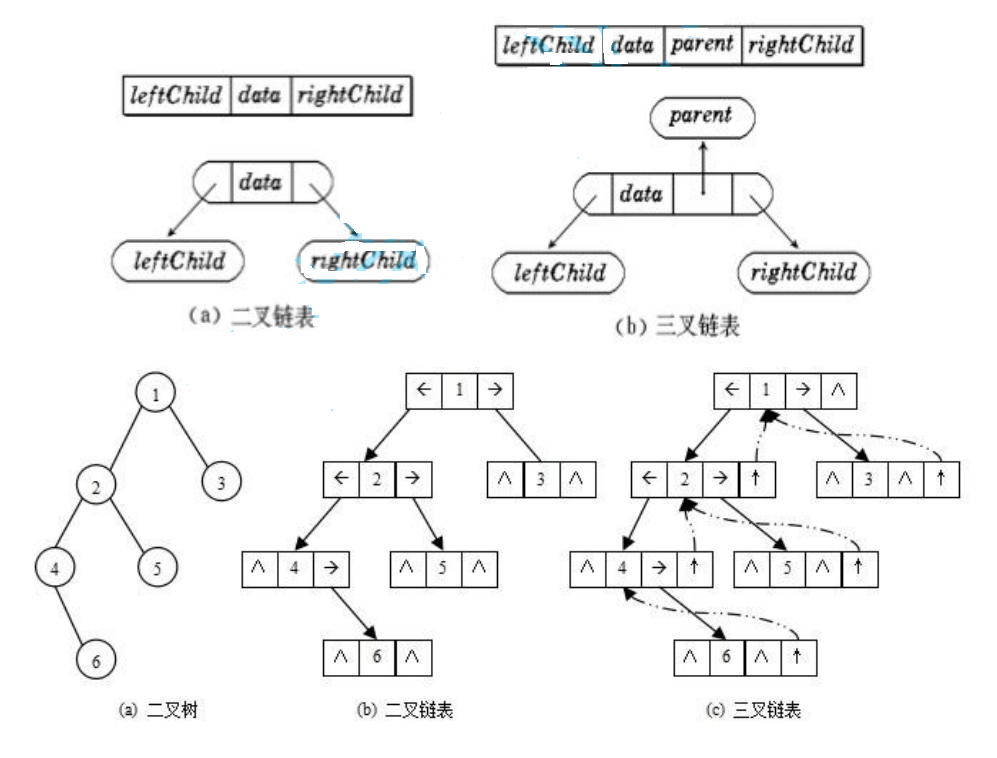
链式存储
二叉树的链式存储结构是指,用链表来表示一棵二叉树,即用链来指示元素的逻辑关系。 通常的方法是链表中每个结点由三个域组成,==数据域和左右指针域==,左右指针分别用来给出该结点左孩子和右孩子所 在的链结点的存储地址 。链式结构又分为二叉链和三叉链。

//代码展示
//二叉链
typedef int BTDateType;
typedef struct BinaryTreeNode
{
BTDateType date;
struct BinaryTreeNode* left;//指向左孩子
struct BinartTreeNode* right;//指向右孩子
}BTNode;
//三叉链
typedef struct BinaryTreeNode
{
BTDateType date; //指向该节点的数据
struct BinaryTreeNode* parent;//指向该节点的双亲
struct BinaryTreeNode* left;//指向左孩子
struct BinaryTreeNode* right;//指向右孩子
}BTNode;
2.二叉树的遍历
学习二叉树结构,最简单的方式就是遍历。所谓二叉树遍历(Traversal)是按照某种特定的规则,依次对二叉 树中的节点进行相应的操作,并且每个节点只操作一次。访问结点所做的操作依赖于具体的应用问题。 遍历 是二叉树上最重要的运算之一,也是二叉树上进行其它运算的基础。
二叉树的三大遍历
前序遍历前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
中序遍历(Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中(间)。
后序遍历(Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。
所以N(Node)、L(Left subtree)和R(Right subtree)又可解释为 根、根的左子树和根的右子树。NLR、LNR和LRN分别又称为先根遍历、中根遍历和后根遍历。
前序遍历:
typedef int BTDateType;
typedef struct BinaryTreeNode
{
BTDateType date;
struct BinaryTreeNode* left;
struct BinartTreeNode* right;
}BTNode;
void PreOrder(BTNode* root)
{
if(root == NULL)
{
printf("NULL ");
return;
}
printf("%d ",root->date);//先访问根
PreOrder(root->left);//再访问左子树
PreOrder(root->right);//最后访问右子树
}
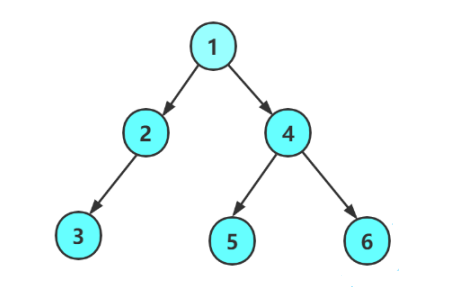
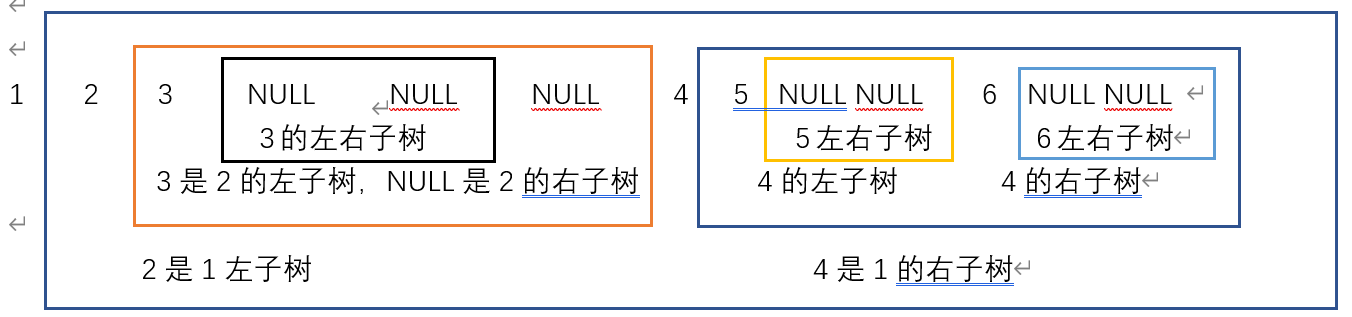
前序遍历流程图
- 前序遍历的特点是第一个一定是根!
中序遍历
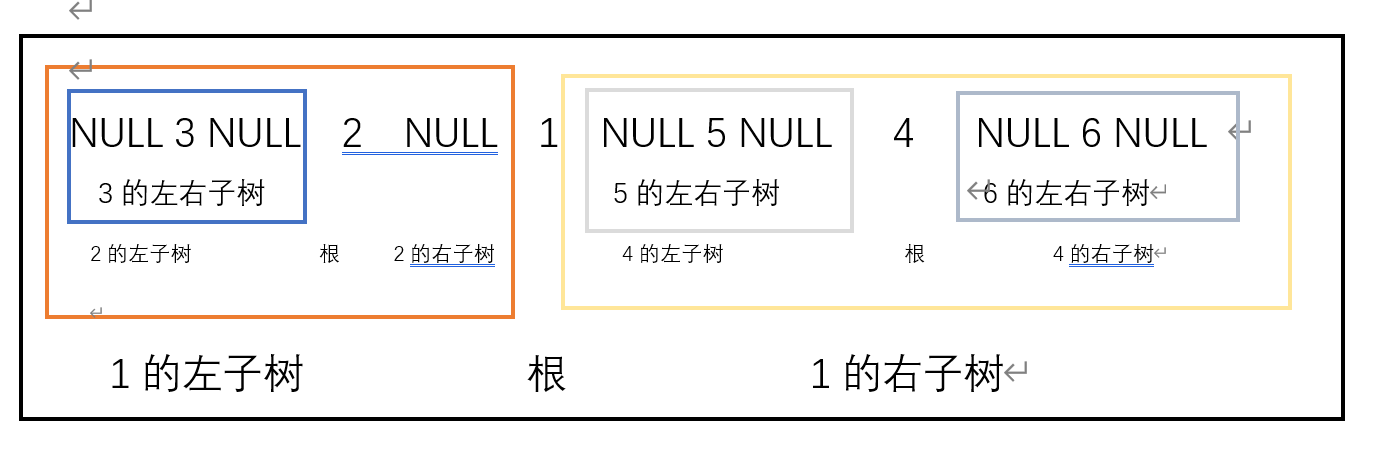
typedef int BTDateType;
typedef struct BinaryTreeNode
{
BTDateType date;
struct BinaryTreeNode* left;
struct BinartTreeNode* right;
}BTNode;
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
PreOrder(root->left);//先访问左子树
printf("%d ", root->date);//再访问根
PreOrder(root->right);//最后访问右子树
}
- 中序遍历的特点是知道根的位置就可以判断出左右子树!
后序遍历
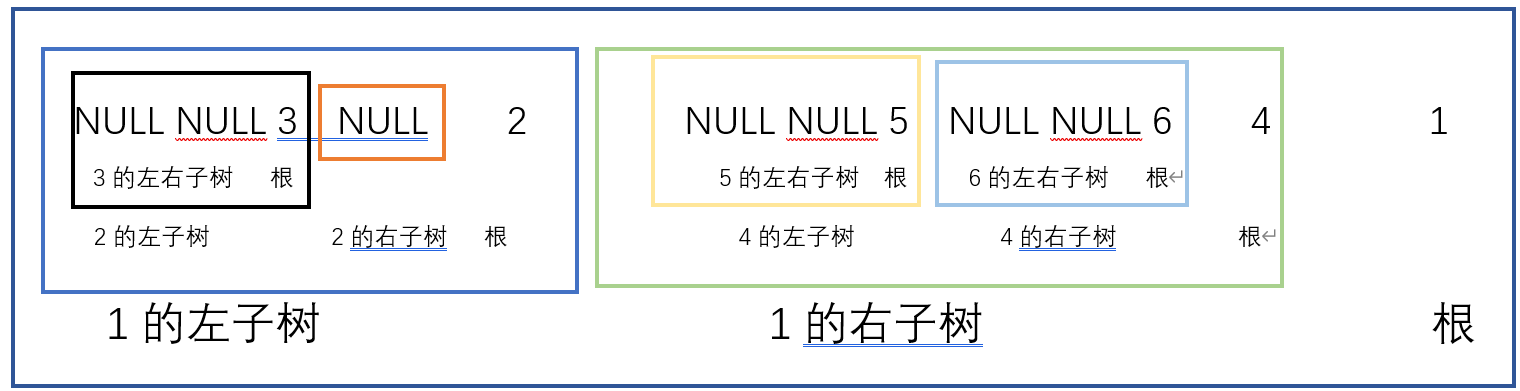
typedef int BTDateType;
typedef struct BinaryTreeNode
{
BTDateType date;
struct BinaryTreeNode* left;
struct BinartTreeNode* right;
}BTNode;
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("NULL ");
return;
}
PreOrder(root->left);//先访问左子树
PreOrder(root->right);//然后访问右子树
printf("%d ", root->date);//最后访问根
}
- 点赞
- 收藏
- 关注作者



评论(0)