计算机各种进制之间的转换，外行人也能看的懂
目录
一、进位计数制
所谓进位计数制也称计数制，是指用一组固定的符号和统一的规则来表示数值
https://baike.baidu.com/item/%E6%95%B0%E5%80%BC的方法。按进位的方法进行计数，称为进位计数制。在计算机中采用的是主要是二进制，此外还有八进制、十进制、十六进制的表示方法。在日常生活中，我们最常用的是十进位计数制，即按照逢十进一的原则进行计数的。
下面先带大家了解一下进制中的基本概念。
一种进位计数制包含一组数码符号和三个基本因素：
* ：一组用来表示某种数制的符号。例如，二进制的数码是0、1 ；八进制的数码是0、1、2、3、4、5、6、7；十进制的数码是0、1、2、3、4、5、6、7、8、9；十六进制的数码是0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F。
* 基数（R）：某种数制可以使用的数码个数。例如，二进制的基数是2，八进制的基数是8；十进制的基数是10； 十六进制的基数是16。
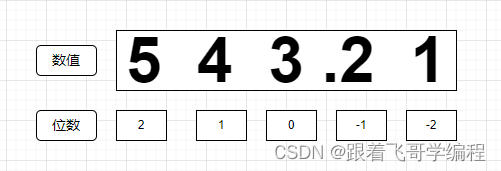
*（i）：数码在一个数中所处的位置，以小数点为中心，小数点左边位数，从右向左依次从0开始，小数点右边位数从左向右依次从-1开始。例如十进制数543.21的每个数字所在位数为
* 权（
）：权是基数（R）的数位（i）次方，表示数码在不同位置上的数值。例如：十进制数值543.21 各位数的权分别为 、、、、。
* 加权计算各位项的合计值为结果值（）： 表示第 i 位的数字。任意进位数的值都可以写为按权展开的多项式的合计。例如 543.21 = 5*+4*+3*+2*+1*。
注：负次方=正次方的倒数，比如=1/。
二、计算机中常用的几种进制
计算机中常用的几种进制，二进制（B）、八进制（O）、十进制（D|不写区分符）、十六进制（H），几进制那么它的基数就是几。
三、进位计数制相互转换
在线进制转换OSCHINA.NET在线工具,ostools为开发设计人员提供在线工具，提供jsbin在线 CSS、JS 调试，在线 Java API文档,在线 PHP API文档,在线 Node.js API文档,Less CSS编译器，MarkDown编译器等其他在线工具
https://tool.oschina.net/hexconvert这里附上在线进制转换工具，方便大家自我练习时验证计算结果是否正确。
1、二进制转八进制
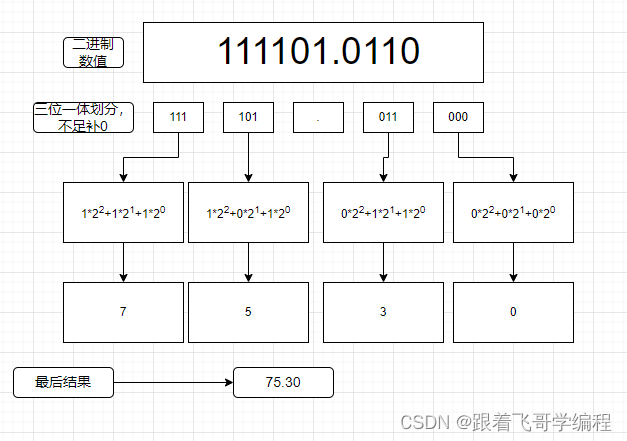
转换规则：以小数点为中心，整数部分从右向左，小数部分从左向右，"三位一体"，不足补0。
思路：先按照3位一体分隔，不足位补0，每3位代表一个值，计算时，每3位从右向左位次为0,1,2
= = 252.74
做个小练习 比如：二进制数 111101.0110 转为8 进制为多少呢？
2、二进制转十进制
转换规则：二进制各位上的系数*对应的权，然后求其和。
例如：二进制111.11转为十进制数，结果为7.75
3、二进制转十六进制
转换规则：以小数点为中心，整数部分从右向左，小数部分从左向右，"四位一体"，不足补0。
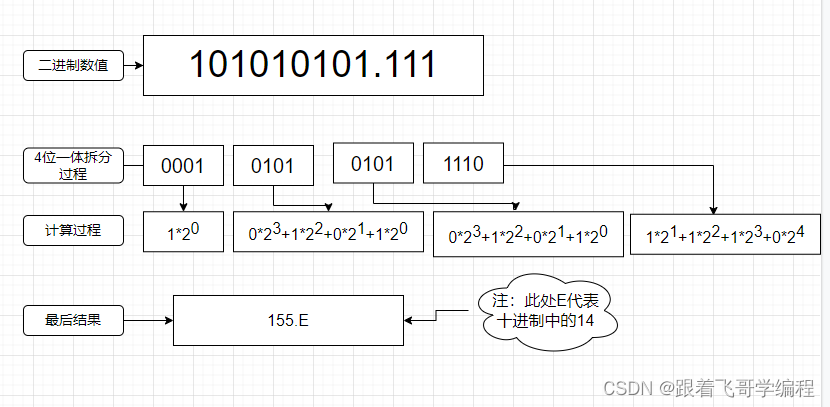
例如：二进制数，101010101.111 转换为 16进制为 155.E
注：上面图例中小数点后的 1110 四位计算过程写错了，应该是从右向左计算，下图纠正的计算过程
注：在十六进制中，只有0~9，A~F 数位。A~F 与 十进制中 10~15 等同。
4、八进制转二进制
转换规则与二进制转八进制正好相反，把八进制上的每一位数一分为三，即为二进制数。
例如：765.43 转为 二进制为 111 110 101 . 100 011
首先八进制数只有0~7 ，那么二进制跟八进制的对应关系表如下，记住即可。
| 二进制 | 八进制 |
|---|---|
| 000 | 0 |
| 001 | 1 |
| 010 | 2 |
| 011 | 3 |
| 100 | 4 |
| 101 | 5 |
| 110 | 6 |
| 111 | 7 |
5、八进制转十进制
转换规则：八进制各位数上的系数*权，再求和。
例如：123.13 转为十进制就是 83.171875
6、八进制转十六进制
转换规则1：先把八进制转成十进制，再把十进制转成十六进制。
转换规则2：先把八进制转成二进制，再把二进制转成十六进制。
例如：八进制数77.77 ，先转成二进制为 111 111.111 111，再转为16进制，此处二进制转16进制为4位一体的分隔规则，为0011 1111. 1111 1100，那么计算为16进制，结果就是 3F.FC。
7、十进制转成 n （n=2，8，16）进制数
转换规则：整数部分除以 n 取余数，倒着写。
小数部分乘以 n 取整数，顺着写。小数部分一般保留三位，末位四舍五入。
例如：十进制数18.55 转十六进制数，结果为：12.852（H）
这里我个人觉得必须掌握十进制转二进制方法。
例如：十进制数18.75 （D）转为二进制数为 10010.11（B）
整数位计算方式： 整数位除以2 取余数直到商为0，那么按照上面计算过程得到的余数，从上到下依次对应二进制整数位的从右到左顺序的值 10010。
0.75*2 = 1.5 取整数 1 对应二进制位小数点后第一位
0.5*2 = 1.0 取整数1 对应二进制位小数点后第二位
小数位计算方式：小数乘以2 取整数位直到所得结果为整数停止，正序对应二进制数位的从左到右顺序的值11
8、十六进制转二进制
转换规则：把十六进制每一位数，一分为四，即可得到二进制数。
例如：十六进制 FEC.BA 转为 二进制为 1111 1110 1100.1011 1010
| 十六进制 | 二进制 |
| 0 | 0000 |
| 1 | 0001 |
| 2 | 0010 |
| 3 | 0011 |
| 4 | 0100 |
| 5 | 0101 |
| 6 | 0110 |
| 7 | 0111 |
| 8 | 1000 |
| 9 | 1001 |
| A | 1010 |
| B | 1011 |
| C | 1100 |
| D | 1101 |
| E | 1110 |
| F | 1111 |
8、十六进制转八进制
转换规则：
先从十六转十进制，再转为八进制
或者
十六转为二进制，再转为八进制
9、十六进制转十进制
转换规则：让十六进制上的各位系数乘以对应的权，然后求和即为十进制数值。
例如：十六进制的 12F.C 转为 十进制 就是 303.75
计算过程如下
个人感觉，最主要需要掌握 二进制 和十进制 之间的转换是最基础的。
四、总结：
- n 进制转 十进制的规则 小数点左侧（系数*n的位次方+系数*n的负位次方）。
注：n进制转十进制时，小数点左侧按照从右向左位次依次为0,1,2...；小数点右侧按照从左到右位次依次为-1，-2，...。
- 二进制转八进制，三位一体分隔；反过来，八进制转二进制，一分为三。
注：二进制转为八进制或十六进制，分割后，计算时，按照从右向左位次，依次为0,1,2
- 二进制转十六进制，四位一体分隔；反过来，十六进制转二进制，一分为四。
- 十进制转二进制，整数部分除以2，取余数，一直到商为0。每次得到的余数按倒序从右向左依次就是二进制小数点左侧的数值。小数部分*2，每次取整数位，直到乘2结果为整数，每次得到的整数位正序从左向右依次就是二进制小数点右侧的数值。
- 点赞
- 收藏
- 关注作者
评论（0）