第一章 前缀和与差分

一、前缀和

1. 题目描述

输入一个长度为 $n$ 的整数序列。

接下来再输入 $m$ 个询问，每个询问输入一对 $l,r$。

对于每个询问，输出原序列中从第 $l$ 个数到第 $r$ 个数的和。

输入格式

第一行包含两个整数 $n$ 和 $m$。

第二行包含 $n$ 个整数，表示整数数列。

接下来 $m$ 行，每行包含两个整数 $l$ 和 $r$，表示一个询问的区间范围。

输出格式

共 $m$ 行，每行输出一个询问的结果。

数据范围

$1≤l≤r≤n$,
$1≤n,m≤100000$,
$−1000≤数列中元素的值≤1000$

输入样例：

5 3
2 1 3 6 4
1 2
1 3
2 4

输出样例：

3
6
10

---

2. 思路分析

具体做法：

1. 首先做一个预处理，定义一个sum[] 数组，sum[i] 代表a数组中前i个数的和。
2. 对于每次查询，只需执行sum[r] - sum[l - 1]。

注意: 前缀和的下标一定要从 1开始, 避免进行下标的转换。

---

3. 代码实现

#include <bits/stdc++.h>

using namespace std;

const int N = 100010;

int n, m;
int a[N], s[N];

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> a[i];
    
    // 前缀和的初始化
    for (int i = 1; i <= n; i ++ ) s[i] = s[i - 1] + a[i];
    
    while (m -- )
    {
        int l, r;
        cin >> l >> r;
        printf("%d\n", s[r] - s[l - 1]); //区间和的计算
    }
    return 0;
}

---

二、子矩阵的和

1. 题目描述

输入一个 $n$ 行 $m$ 列的整数矩阵，再输入 $q$ 个询问，每个询问包含四个整数 $x1,y1,x2,y2$，表示一个子矩阵的左上角坐标和右下角坐标。

对于每个询问输出子矩阵中所有数的和。

输入格式

第一行包含三个整数 $n，m，q$。

接下来 $n$ 行，每行包含 $m$ 个整数，表示整数矩阵。

接下来 $q$ 行，每行包含四个整数 $x1,y1,x2,y2$，表示一组询问。

输出格式

共 $q$ 行，每行输出一个询问的结果。

数据范围

$1≤n,m≤1000$,
$1≤q≤200000$,
$1≤x1≤x2≤n$,
$1≤y1≤y2≤m$,
$−1000≤矩阵内元素的值≤1000$

输入样例：

3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4

输出样例：

17
27
21

---

2. 思路分析

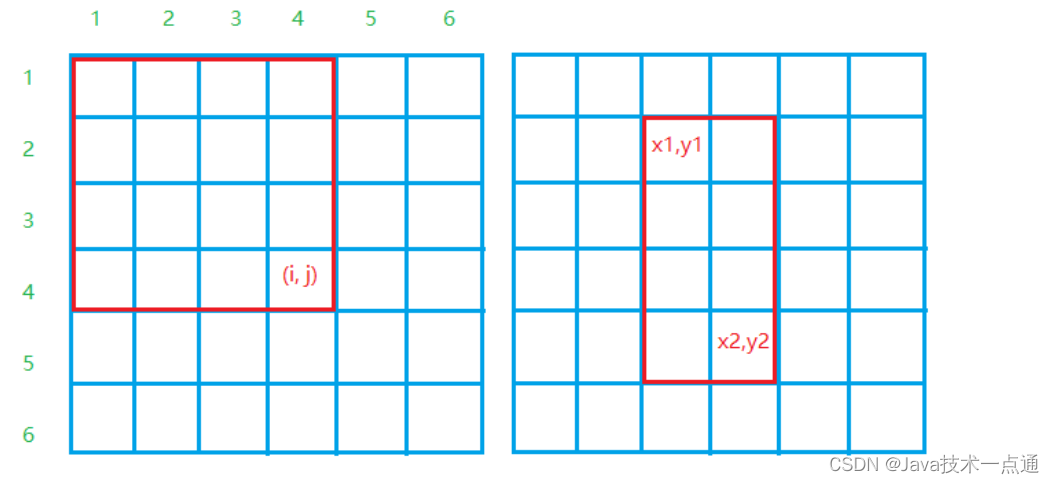
1. $S[i,j]$ 即为图1红框中所有数的的和为：
   s[i][j] = s[i][j - 1] + s[i - 1][j] - s[i - 1][j - 1] + a[i][j]

2. $(x1,y1),(x2,y2)$这一子矩阵中的所有数之和为：
   s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1]

---

3. 代码实现

#include <bits/stdc++.h>

using namespace std;

const int N = 1010;

int n, m, q;
int a[N][N], s[N][N];

int main()
{
    cin >> n >> m >> q;
    
    for (int i = 1; i <= n; i ++)
        for (int j = 1; j <= m; j ++ )
            cin >> a[i][j];
    
    for (int i = 1; i <= n; i ++ )
        for (int j = 1; j <= m; j ++ )
             s[i][j] = s[i][j - 1] + s[i - 1][j] - s[i - 1][j - 1] + a[i][j];
    
    while (q -- )
    {
        int x1, y1, x2, y2;
        cin >> x1 >> y1 >> x2 >> y2;
        cout << s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1  - 1] << endl;
    }
    return 0;
}

---

三、差分

1. 题目描述

输入一个长度为 $n$ 的整数序列。

接下来输入 $m$ 个操作，每个操作包含三个整数 $l,r,c$，表示将序列中 $[l,r]$ 之间的每个数加上 $c$。

请你输出进行完所有操作后的序列。

输入格式

第一行包含两个整数 $n$ 和 $m$。

第二行包含 $n$ 个整数，表示整数序列。

接下来 $m$ 行，每行包含三个整数 $l，r，c$，表示一个操作。

输出格式

共一行，包含 $n$ 个整数，表示最终序列。

数据范围

$1≤n,m≤100000$,
$1≤l≤r≤n$,
$−1000≤c≤1000$,
$−1000≤整数序列中元素的值≤1000$

输入样例：

6 3
1 2 2 1 2 1
1 3 1
3 5 1
1 6 1

输出样例：

3 4 5 3 4 2

---

2. 思路分析

差分思想和前缀和是相反的。

首先我们先定义数组a, 其中a[1],a[2]…a[n]作为前缀和。

然后构造数组b，b[1],b[2]…b[n]为差分数组。其中通过差分数组的前缀和来表示a数组，即a[n] = b[1] + b[2]+…+b[n]。

一维差分数组的构造也很简单，即a[1] = b[1], b[2] = a[2] - a[1], b[n] = a[n] - a[n-1]；

注意： 刚开始时可以初始化数组a, b全部为0，输入a数组后；在构造时，只需要将b[1]看做在[1, 1]区间上加上a[1]; b[2] 看作在[2, 2]区间上加上a[2]。

//对于b[1]:
b[1] = 0 + a[1];
b[2] = 0 - a[1]; 	//最终：b[1] = a[1]
//对于b[2]:
b[2] = b[2] + a[2];  //==> 最终：b[2] = a[2] - a[1]
b[3] = b[3] - b[2];

---

3. 代码实现

#include <bits/stdc++.h>

using namespace std;

const int N = 100010;

int n, m;
int a[N], b[N];

void insert(int l, int r, int c)
{
    b[l] += c;
    b[r + 1] -= c;
}

int main()
{
    cin >> n >> m;
    for (int i = 1; i <= n; i ++ ) cin >> a[i];
    
    //构造差分数组，b[i]看作是在[i,i]区间加上a[i]
    for (int i = 1; i <= n; i ++ ) insert(i, i, a[i]);
    
    while (m -- )
    {
        int l, r, c;
        cin >> l >> r >> c;
        insert(l, r, c);;
    }
    
    //前缀和
    for (int i = 1; i <= n; i ++ ) b[i] += b[i - 1];
    
    for (int i = 1; i <= n; i ++ ) cout  << b[i] << ' ';
    
    return 0;
} 

---

第二章 双指针算法

一、最长连续不重复子序列

1. 题目描述

给定一个长度为 $n$ 的整数序列，请找出最长的不包含重复的数的连续区间，输出它的长度。

输入格式

第一行包含整数 $n$。

第二行包含 $n$ 个整数（均在 $0∼10^5$ 范围内），表示整数序列。

输出格式

共一行，包含一个整数，表示最长的不包含重复的数的连续区间的长度。

数据范围

$1≤n≤10^5$
输入样例：

5
1 2 2 3 5

输出样例：

3

---

2. 思路分析

1. 遍历数组中的每一个元素a[i]，将每一个元素出现的次数存储在 $q$中；
2. 找到 $j$使得双指针 $[j, i]$ 维护的是以 a[i] 结尾的最长连续不重复子序列，长度为 $i - j + 1$, 将这一长度与 $res$的较大者更新给 $res$。

3. 代码实现

#include <bits/stdc++.h>

using namespace std;

const int N = 100010;

int n;
int q[N], s[N];

int main()
{
    cin >> n;
    for (int i = 0; i < n; i ++ ) cin >> q[i];
    
    int res = 0;
    for (int i = 0, j = 0; i < n; i ++ )
    {
        s[q[i]] ++;
        while (j < i && s[q[i]] > 1) s[q[j ++]] --;
        res = max(res, i - j + 1);
    }
    cout << res << endl;
    return 0;
}

---

二、数组元素的目标和

1. 题目描述

给定两个升序排序的有序数组 $A$ 和 $B$，以及一个目标值 $x$。

数组下标从 $0$ 开始。

请你求出满足 $A[i]+B[j]=x$ 的数对 $(i,j)$。

数据保证有唯一解。

输入格式

第一行包含三个整数 $n,m,x$，分别表示 $A$ 的长度， $B$ 的长度以及目标值 $x$。

第二行包含 $n$ 个整数，表示数组 $A$。

第三行包含 $m$ 个整数，表示数组 $B$。

输出格式

共一行，包含两个整数 $i$ 和 $j$。

数据范围

数组长度不超过 $10^5$。
同一数组内元素各不相同。
$1≤数组元素≤10^9$

输入样例：

4 5 6
1 2 4 7
3 4 6 8 9

输出样例：

1 1

---

2. 思路分析

1. 定义一个指针 $i$ 指向数组 $A$ 的头部进行枚举，再定义一个指针 $j$ 指向数组 $B$ 的尾部进行 枚举；
2. 由于数组都是单调递增的，若 $A[i] + b[j] > x$，则执行 $j --$;
3. 如果 $A[i] + b[j] = x$，则直接输出数对 $(i,j)$。

3. 代码实现

#include <bits/stdc++.h>

using namespace std;

const int N = 1e5 + 10;

int n, m, x;
int a[N], b[N];

int main()
{
    cin >> n >> m >> x;
    for (int i = 0; i < n; i ++ ) cin >> a[i];
    for (int i = 0; i < m; i ++ ) cin >> b[i];
    
    for (int i = 0, j = m - 1; i < n; i ++ )
    {
        // 由于a[],b[]均为严格上升数组，所以如果a[i] + b[j] > x的话就让j --
        while (j >= 0 && a[i] + b[j] > x) j --;
        //如果a[i] + b[j] = x，则直接输出数对（i,j）
        if (j >= 0 && a[i] + b[j] == x) cout << i << ' ' << j << endl;
    }
    
    return 0;
}

---

三、判断子序列

1. 题目描述

给定一个长度为 $n$ 的整数序列 $a1,a2,…,an$ 以及一个长度为 $m$ 的整数序列 $b1,b2,…,bm$。

请你判断 $a$ 序列是否为 $b$ 序列的子序列。

子序列指序列的一部分项按原有次序排列而得的序列，例如序列 ${a1,a3,a5}$ 是序列 ${a1,a2,a3,a4,a5}$ 的一个子序列。

输入格式

第一行包含两个整数 $n,m$。

第二行包含 $n$ 个整数，表示 $a1,a2,…,an$。

第三行包含 $m$ 个整数，表示 $b1,b2,…,bm$。

输出格式

如果 $a$ 序列是 $b$ 序列的子序列，输出一行 Yes。

否则，输出 No。

数据范围

$1≤n≤m≤10^5$,
$−10^9≤ai,bi≤10^9$

输入样例：

3 5
1 3 5
1 2 3 4 5

输出样例：

Yes

---

2. 思路分析

1. 定义指针 $i$ 来扫描 $a$ 数组，指针 $j$ 来扫描 $b$ 数组；
2. 如 $a[i] == b[j]$ 时，则让指针 $i$ 往后移动一位；
3. 整个过程中指针 $j$ 不断往后移动，而指针 $i$ 只有匹配成功才后移一位，若最后 $i == n$，则说明匹配成功。

---

3. 代码实现

#include <bits/stdc++.h>

using namespace std;

const int N = 100010;

int n, m;
int a[N], b[N];

int main()
{
    cin >> n >> m;
    for (int i = 0; i < n; i ++ ) cin >> a[i];
    for (int i = 0; i < m; i ++ ) cin >> b[i];
    
    int i = 0, j = 0;
    while (i < n && j < m)
    {
        if (a[i] == b[j]) i ++;
        j ++;
    } 
    if (i == n) puts("Yes");
    else puts("No");
    
    return 0;
}

---

第三章 位运算

一、二进制中1的个数

1. 题目描述

给定一个长度为 $n$ 的数列，请你求出数列中每个数的二进制表示中 $1$ 的个数。

输入格式

第一行包含整数 $n$。

第二行包含 $n$ 个整数，表示整个数列。

输出格式

共一行，包含 $n$ 个整数，其中的第 $i$ 个数表示数列中的第 $i$ 个数的二进制表示中 $1$ 的个数。

数据范围

$1≤n≤100000$,
$0≤数列中元素的值≤10^9$

输入样例：

5
1 2 3 4 5

输出样例：

1 1 2 1 2

---

2. 思路分析

使用lowbit操作，每次lowbit操作截取一个数字最后一个1后面的所有位，每次减去lowbit得到的数字，直到数字减到0，就得到了最终1的个数。
例如：0000100100经过lowbit操作后就会取出最后一个1后面的所有位，即100。

---

3. 代码实现

#include <bits/stdc++.h>

using namespace std;;

int main()
{
    int n;
    cin >> n;
    while (n -- )
    {
        int x, s = 0;
        cin >> x;
        
        for (int i = x; i; i -= i & -i) s ++;
        
        cout << s << ' ';
    }
    return 0;
}

---

第四章 离散化

待完善......

---

第五章 区间和并

一、区间合并

1. 题目描述

给定 $n$ 个区间 $[l_i,r_i]$，要求合并所有有交集的区间。

注意如果在端点处相交，也算有交集。

输出合并完成后的区间个数。

例如： $[1,3]$ 和 $[2,6]$ 可以合并为一个区间 $[1,6]$。

输入格式

第一行包含整数 $n$。

接下来 $n$ 行，每行包含两个整数 $l$ 和 $r$。

输出格式

共一行，包含一个整数，表示合并区间完成后的区间个数。

数据范围

$1≤n≤100000$,
$−10^9≤l_i≤r_i≤10^9$

输入样例：

5
1 2
2 4
5 6
7 8
7 9

输出样例：

3

---

2. 思路分析

1. 将各区间先按左端点从小到大进行排序；

2. 再维护一个区间，与后面一个个区间进行三种情况的比较，存储到数组里去。

   • 情况一： 当前区间完全覆盖下一区间，直接跳过；
   • 情况二： 将当前区间的右端点更新为下一区间的右端点，达到区间延长的效果；
   • 情况三： 当前区间的右端点严格小于下一区间的左端点，将当前区间存储到数组中，并且更新当前区间为下一区间。

3. 最后返回数组的长度即可，即为合并后剩下几个集合。

---

3. 代码实现

#include <bits/stdc++.h>

using namespace std;

typedef pair<int, int> PII;

void merge(vector<PII> &segs)
{
    vector<PII> res;

    //按左端点进行排序
    sort(segs.begin(), segs.end());

    //st代表区间开头，ed代表区间结尾
    
    int st = -2e9, ed = -2e9;
    for (auto seg : segs)
        //情况三：两个区间无法合并
        if (ed < seg.first)
        {
            if (st != -2e9) res.push_back({st, ed}); //将当前区间加入数组
            st = seg.first, ed = seg.second; //更新新的区间
        }
        //情况二：更新区间右端点
        else ed = max(ed, seg.second);
    
    //将最后的当前区间加入数组
    //判断：防止输入的区间为空
    if (st != -2e9) res.push_back({st, ed});

    segs = res;
}

int main()
{
    int n;
    scanf("%d", &n);

    vector<PII> segs;
    for (int i = 0; i < n; i ++ )
    {
        int l, r;
        scanf("%d%d", &l, &r);
        segs.push_back({l, r});
    }

    merge(segs);

    cout << segs.size() << endl;

    return 0;
}

---

创作不易，如果有帮助到你，请给文章==点个赞和收藏==，让更多的人看到！！！
==关注博主==不迷路，内容持续更新中。