0.前言召回排序流程策略算法简介

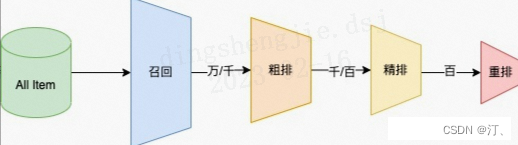
推荐可分为以下四个流程，分别是召回、粗排、精排以及重排：

1. 召回是源头，在某种意义上决定着整个推荐的天花板；
2. 粗排是初筛，一般不会上复杂模型；
3. 精排是整个推荐环节的重中之重，在特征和模型上都会做的比较复杂；
4. 重排，一般是做打散或满足业务运营的特定强插需求，同样不会使用复杂模型；

• 召回层：召回解决的是从海量候选item中召回千级别的item问题

  • 统计类，热度，LBS；
  • 协同过滤类，UserCF、ItemCF；
  • U2T2I，如基于user tag召回；
  • I2I类，如Embedding（Word2Vec、FastText），GraphEmbedding（Node2Vec、DeepWalk、EGES）；
  • U2I类，如DSSM、YouTube DNN、Sentence Bert；
    

• 模型类：模型类的模式是将用户和item分别映射到一个向量空间，然后用向量召回，这类有itemcf，usercf，embedding（word2vec），Graph embedding（node2vec等），DNN（如DSSM双塔召回，YouTubeDNN等），RNN（预测下一个点击的item得到用户emb和item emb）；向量检索可以用Annoy（基于LSH），Faiss（基于矢量量化）。此外还见过用逻辑回归搞个预估模型，把权重大的交叉特征拿出来构建索引做召回

• 排序策略，learning to rank 流程三大模式（pointwise、pairwise、listwise），主要是特征工程和CTR模型预估；

  • 粗排层：本质上跟精排类似，只是特征和模型复杂度上会精简，此外也有将精排模型通过蒸馏得到简化版模型来做粗排
    • 常见的特征挖掘（user、item、context，以及相互交叉）；
  • 精排层：精排解决的是从千级别item到几十这个级别的问题
    • CTR预估：lr，gbdt，fm及其变种（fm是一个工程团队不太强又对算法精度有一定要求时比较好的选择），widedeep，deepfm，NCF各种交叉，DIN，BERT，RNN
    • 多目标：MOE，MMOE，MTL（多任务学习）
    • 打分公式融合: 随机搜索，CEM（性价比比较高的方法），在线贝叶斯优化（高斯过程），带模型CEM，强化学习等
      

• 重排层：重排层解决的是展示列表总体最优，模型有 MMR，DPP，RNN系列（参考阿里的globalrerank系列）

• 展示层：

  • 推荐理由：统计规则、行为规则、抽取式（一般从评论和内容中抽取）、生成式；排序可以用汤普森采样（简单有效），融合到精排模型排等等
  • 首图优选：CNN抽特征，汤普森采样

• 探索与利用：随机策略（简单有效），汤普森采样，bandit，强化学习（Q-Learning、DQN）等

• 产品层：交互式推荐、分tab、多种类型物料融合

粗排与精排就像级联漏斗，两者目标更多保持同向一致性，粗排就是跟精排保持步调一致。如果粗排排序高的，精排排序也高，那么粗排就很好的完成了“帮助精排缓冲”的目的。而rerank环节类似于排序改判：可能涉及业务调整、打散、强插、增量分等等。

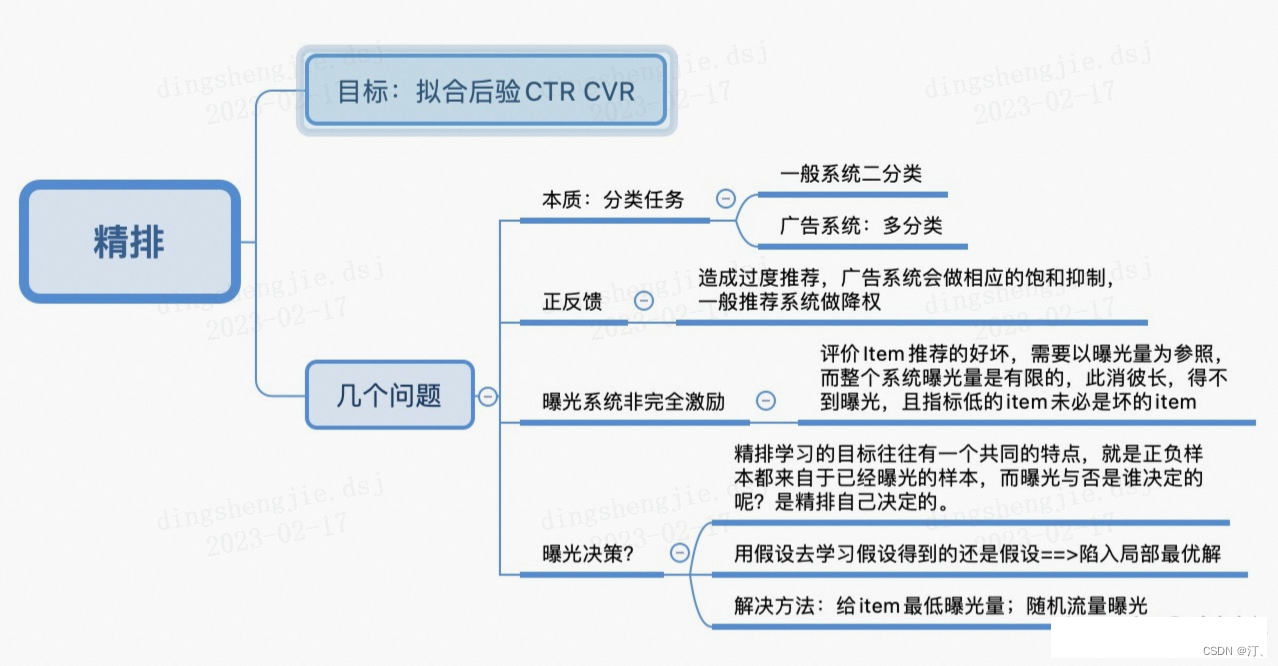
1.精排简介

Learning to Rank (LTR)是一类技术方法，主要利用机器学习算法解决实际中的排序问题。传统的机器学习主要解决的问题是一个分类或者回归问题，比如对一个样本数据预测对应的类别或者预测一个数值分值。而LTR解决的是一个排序问题，对一个list的item进行一个排序，所以LTR并不太关注这个list的每个item具体得多少分值，更关注所有item的相对顺序。排序通常是信息检索的核心成分，所以LTR最常见的应用是搜索场景，对召回的document进行排序。

1.1 精排应用场景

排序学习场景：

• 推荐系统，基于历史行为的“猜你喜欢”
• 搜索排序，基于某Query进行的结果排序，期望用户选中的在排序结果中是靠前的 => 有意识的被动推荐
• 排序结果都很重要，猜用户想要点击或者booking的item就在结果列表前面
• 排序学习是个性化结果，用于搜索列表、推荐列表、广告等场景

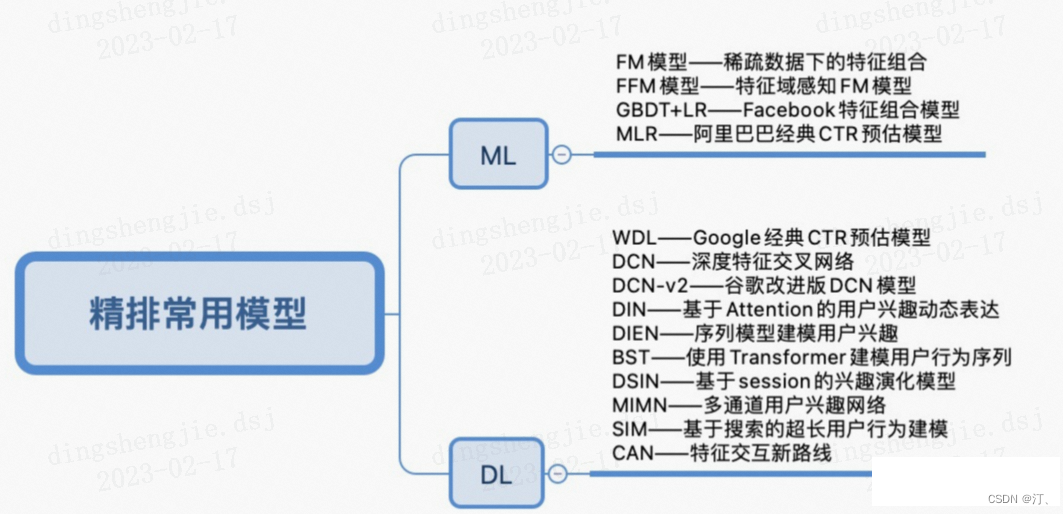
1.2 常用模型

排序模型按照结构划分，可以分为线性排序模型、树模型、深度学习模型：
从早期的线性模型LR，到引入自动二阶交叉特征的FM和FFM，到非线性树模型GBDT和GBDT+LR，到最近全面迁移至大规模深度学习排序模型。

• 线性排序模型：LR
• 树模型：GBDT,GBDT+LR, LambdaMART
• 深度学习模型: DeepFM,Wide&Deep, ListNet, AdaRank，SoftRank，LambdaRank等

2.LTR三大结构：Pointwise, Pairwise, Listwise

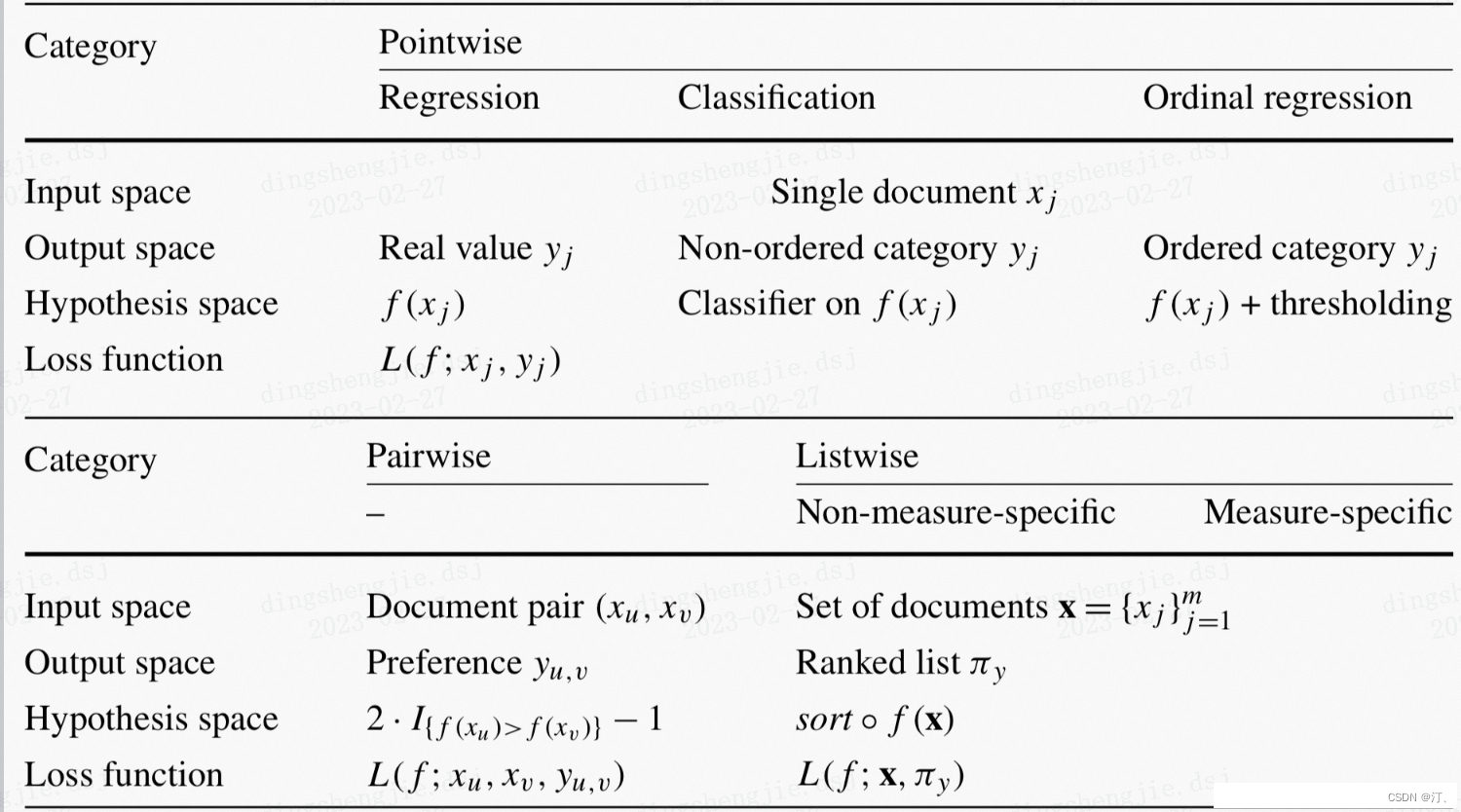
序模型按照样本生成方法和损失函数loss的不同，可以划分成Pointwise, Pairwise, Listwise三类方法：

• Pointwise排序学习（单点法）：
  • 将训练样本转换为多分类问题（样本特征-类别标记）或者回归问题（样本特征-连续值）
  • 只考虑单个样本的好坏，没有考虑样本之间的顺序
• Pairewise排序学习（配对法）：
  • 比较流行的LTR学习方法，将排序问题转换为二元分类问题
  • 接收到用户査询后，返回相关文档列表，确定文档之间的先后顺序关系（多个pair的排序问题），只考虑了两个文档的相对顺序，没有考虑文档在搜索列表中的位置。
• Listwise排序学习（列表法）：
  • 它是将每个Query对应的所有搜索结果列表作为一个训练样例
  • 根据训练样例训练得到最优评分函数F，对应新的查询，评分F对每个文档打分，然后根据得分由高到低排序，即为最终的排序结果

2.1 pointwise

pointwise将其转化为多类分类或者回归问题

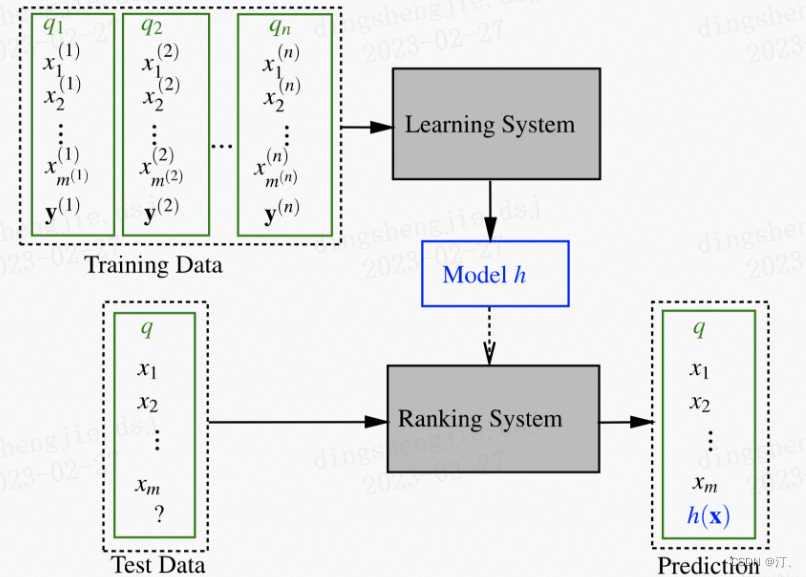
Pointwise 类方法，其 L2R 框架具有以下特征：

• 输入空间中样本是单个 doc（和对应 query）构成的特征向量；
• 输出空间中样本是单个 doc（和对应 query）的相关度；
• 假设空间中样本是打分函数；
• 损失函数评估单个 doc 的预测得分和真实得分之间差异。

这里讨论下，关于人工标注标签怎么转换到 pointwise 类方法的输出空间：

• 如果标注直接是相关度 $s_j$，则 $doc x_j$ 的真实标签定义为 $y_j=s_j$
• 如果标注是 pairwise preference $s_{u,v}$，则 $doc x_j$ 的真实标签可以利用该 doc 击败了其他 docs 的频次
• 如果标注是整体排序 π，则 $doc x_j$ 的真实标签可以利用映射函数，如将 doc 的排序位置序号当作真实标签

2.1.1 算法简介

根据使用的 ML 方法不同，pointwise 类可以进一步分成三类：基于回归的算法、基于分类的算法，基于有序回归的算法。下面详细介绍。

1. 基于回归的算法
   此时，输出空间包含的是实值相关度得分。
   采用 ML 中传统的回归方法即可。

2. 基于分类的算法
   此时，输出空间包含的是无序类别。
   对于二分类，SVM、LR 等均可；对于多分类，提升树等均可。

3. 基于有序回归的算法
   此时，输出空间包含的是有序类别。
   通常是找到一个打分函数，然后用一系列阈值对得分进行分割，得到有序类别。采用 PRanking、基于 margin 的方法都可以。

2.1.2 ponitwise 细则

pointwise方法损失函数计算只与单个document有关，本质上是训练一个分类模型或者回归模型，判断这个document与当前的这个query相关程度，最后的排序结果就是从模型对这些document的预测的分值进行一个排序。对于pointwise方法，给定一个query的document list，对于每个document的预测与其它document是独立的。所以模型输入和对应的标签label形式如下：

• 输入: 单个document
• 标签label: document所属类型或者分值
  pointwise方法将排序任务看做对单个文本的回归或者分类任务来做。若文档document的相关性等级有K种，则我们可以建模为一个有K个类别的 $\{0,1,2,..., K-1\}$的Multi-class分类任务，则 $y_i \in \R^k$
  一个k维度的one-hot表示, 我们可以用交叉熵loss作为目标损失函数:

$\left.\mathrm{L}=-\left(\mathrm{y}_{\mathrm{i}} \log \left(\mathrm{p}_{\mathrm{i}}\right)-\left(1-\mathrm{y}_{\mathrm{i}}\right) \log \left(1-\mathrm{p}_{\mathrm{i}}\right)\right]\right)$

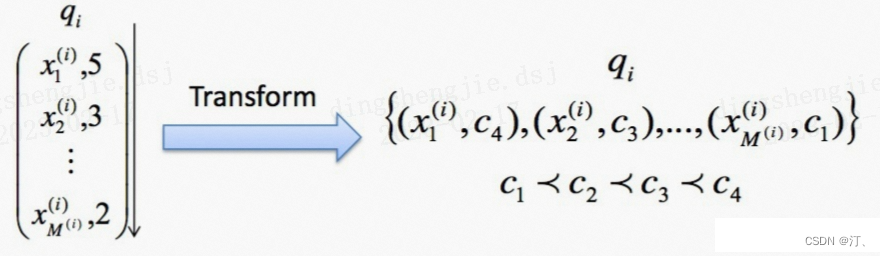
参考链接：https://zhuanlan.zhihu.com/p/528533867

2.1.3 Pointwise排序学习（单点法）总结：

1. 将文档转化为特征向量，每个文档都是独立的
2. 对于某一个query，它将每个doc分别判断与这个query的相关程度
3. 将docs排序问题转化为了分类（比如相关、不相关）或回归问题（相关程度越大，回归函数的值越大）
4. 从训练数据中学习到的分类或者回归函数对doc打分，打分结果即是搜索结果，CTR可以采用Pointwise方式进行学习，对每一个候选item给出一个评分，基于评分进行排序
5. 仅仅考虑了query和doc之间的关系，而没有考虑排序列表中docs之间的关系
6. 主要算法：转换为回归问题，使用LR，GBDT，Prank, McRank

缺陷

• ranking 追求的是排序结果，并不要求精确打分，只要有相对打分即可。
• pointwise 类方法并没有考虑同一个 query 对应的 docs 间的内部依赖性。一方面，导致输入空间内的样本不是 IID 的，违反了 ML 的基本假设，另一方面，没有充分利用这种样本间的结构性。其次，当不同 query 对应不同数量的 docs 时，整体 loss 将会被对应 docs 数量大的 query 组所支配，前面说过应该每组 query 都是等价的。
• 损失函数也没有 model 到预测排序中的位置信息。因此，损失函数可能无意的过多强调那些不重要的 docs，即那些排序在后面对用户体验影响小的 doc。

改进

• Pointwise 类算法也可以再改进，比如在 loss 中引入基于 query 的正则化因子的 RankCosine 方法。

2.2 pairwise

pairwise将其转化为pair分类问题

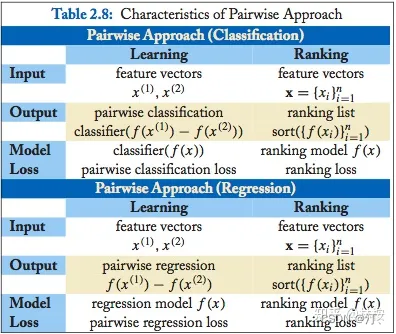
Pairwise 类方法，其 L2R 框架具有以下特征：

• 输入空间中样本是（同一 query 对应的）两个 doc（和对应 query）构成的两个特征向量；

• 输出空间中样本是 pairwise preference；

• 假设空间中样本是二变量函数；

• 损失函数评估 doc pair 的预测 preference 和真实 preference 之间差异。
  这里讨论下，关于人工标注标签怎么转换到 pairwise 类方法的输出空间：

• 如果标注直接是相关度 $s_j$，则 doc $pair (x_u,x_v)$ 的真实标签定义为 $y_{u,v}=2*I_{s_u>s_v}-1$

• 如果标注是 pairwise preference $s_{u,v}$，则 doc $pair (x_u,x_v)$ 的真实标签定义为 $y_{u,v}=s_{u,v}$

• 如果标注是整体排序 π，则 doc $pair (x_u,x_v)$ 的真实标签定义为 $y_{u,v}=2*I_{π_u,π_v}-1$

2.2.1 算法简介

1. 基于二分类的算法
   pairwise 类方法基本就是使用二分类算法即可。
   经典的算法有 基于 NN 的 SortNet，基于 NN 的 RankNet，基于 fidelity loss 的 FRank，基于 AdaBoost 的 RankBoost，基于 SVM 的 RankingSVM，基于提升树的 GBRank。

2.2.2 pairwise细则

基于pairwise的方法，在计算目标损失函数的时候，每一次需要基于一个pair的document的预测结果进行损失函数的计算。比如给定一个pair对的document，优化器需要优化的是两个document的排序关系，与groud truth的排序顺序保持一致。目标是最小化与groud truth不一致的排序对。在实际应用中，pairwise方法比pointwise效果更好，因为预测相对的排序相比预测一个类别或者一个分值，更符合排序的性质。其中模型输入和对应的标签label形式如下：

• 输入: 一个pair对document (A,B)
• 输出标签: 相对顺序label (1, 0.5, 0)

其中1表示相关性等级A>B，0.5表示相关性等级A=B，0表示相关性等级A<B。

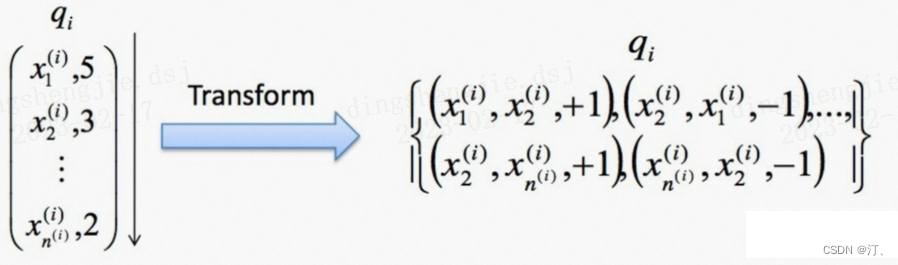
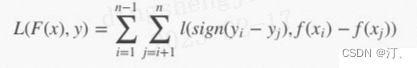
2.2.3 Pairewise排序学习（配对法）总结：

1. 比较流行的LTR学习方法，将排序问题转换为二元分类问题
2. 接收到用户査询后，返回相关文档列表，确定文档之间的先后顺序关系（多个pair的排序问题）
3. 对于同一查询的相关文档集中，对任何两个不同label的文档，都可以得到一个训练实例 $（di,dj）$，如果 $di>dj$则赋值+1，反之-1
4. 没有考虑文档出现在搜索列表中的位置，排在搜索结果前面的文档更为重要，如果靠前的文档出现判断错误，代价会很高

1. 缺点：
虽然 pairwise 类相较 pointwise 类 model 到一些 doc pair 间的相对顺序信息，但还是存在不少问题，回顾概述中提到的评估指标应该基于 query 和 position，

• 如果人工标注给定的是第一种和第三种，即已包含多有序类别，那么转化成 pairwise preference 时必定会损失掉一些更细粒度的相关度标注信息。
• doc pair 的数量将是 doc 数量的二次，从而 pointwise 类方法就存在的 query 间 doc 数量的不平衡性将在 pairwise 类方法中进一步放大。
• pairwise 类方法相对 pointwise 类方法对噪声标注更敏感，即一个错误标注会引起多个 doc pair 标注错误。
• pairwise 类方法仅考虑了 doc pair 的相对位置，损失函数还是没有 model 到预测排序中的位置信息。
• pairwise 类方法也没有考虑同一个 query 对应的 doc pair 间的内部依赖性，即输入空间内的样本并不是 IID 的，违反了 ML 的基本假设，并且也没有充分利用这种样本间的结构性。

2. 改进
pairwise 类方法也有一些尝试，去一定程度解决上述缺陷，比如：

• Multiple hyperplane ranker，主要针对前述第一个缺陷
• magnitude-preserving ranking，主要针对前述第一个缺陷
• IRSVM，主要针对前述第二个缺陷
• 采用 Sigmoid 进行改进的 pairwise 方法，主要针对前述第三个缺陷
• P-norm push，主要针对前述第四个缺陷
• Ordered weighted average ranking，主要针对前述第四个缺陷
• LambdaRank，主要针对前述第四个缺陷
• Sparse ranker，主要针对前述第四个缺陷

2.3 listwise

Listwise 类方法，其 L2R 框架具有以下特征：

• 输入空间中样本是（同一 query 对应的）所有 doc（与对应的 query）构成的多个特征向量（列表）；
• 输出空间中样本是这些 doc（和对应 query）的相关度排序列表或者排列；
• 假设空间中样本是多变量函数，对于 docs 得到其排列，实践中，通常是一个打分函数，根据打分函数对所有 docs 的打分进行排序得到 docs 相关度的排列；
• 损失函数分成两类，一类是直接和评价指标相关的，还有一类不是直接相关的。具体后面介绍。

这里讨论下，关于人工标注标签怎么转换到 listwise 类方法的输出空间：

• 如果标注直接是相关度 $s_j$，则 doc set 的真实标签可以利用相关度 $s_j$进行比较构造出排列
• 如果标注是 pairwise preference $s_{u,v}$，则 doc set 的真实标签也可以利用所有 $s_{u,v}$进行比较构造出排列
• 如果标注是整体排序 π，则 doc set 则可以直接得到真实标签

2.3.1 算法简介

1. 直接基于评价指标的算法

直接取优化 ranking 的评价指标，也算是 listwise 中最直观的方法。但这并不简单，因为前面说过评价指标都是离散不可微的，具体处理方式有这么几种：

• 优化基于评价指标的 ranking error 的连续可微的近似，这种方法就可以直接应用已有的优化方法，如SoftRank，ApproximateRank，SmoothRank
• 优化基于评价指标的 ranking error 的连续可微的上界，如 SVM-MAP，SVM-NDCG，PermuRank
• 使用可以优化非平滑目标函数的优化技术，如 AdaRank，RankGP

上述方法的优化目标都是直接和 ranking 的评价指标有关。现在来考虑一个概念，informativeness。通常认为一个更有信息量的指标，可以产生更有效的排序模型。而多层评价指标（NDCG）相较二元评价（AP）指标通常更富信息量。因此，有时虽然使用信息量更少的指标来评估模型，但仍然可以使用更富信息量的指标来作为 loss 进行模型训练。

通过直接优化排序结果中的评测指标来优化排序任务，但是基于评测指标比如NDCG依赖排序结果，是不连续不可导的。所以优化这些不连续不可导的目标函数面临较大的挑战，目前多数优化技术都是基于函数可导的情况。那么如何解决这个问题？常见的有如下两种方法：

• 通过使用优化技术将目标函数转变成连续可导的函数，然后进行求解，比如SoftRank和 AdaRank等模型
• 通过使用优化技术对非连续的不可导目标函数就行求解，比如 LambdaRank

LambdaRank
RankNet优化目标是最小化pair对错误，但是在信息检索领域比如NDCG这样的评测指标，这样的优化目标并不能够最大化效果，通常在信息检索中我们更关注的是topN的排序结果，且相关性越大的文本最需要排在最前面。如下图所示：

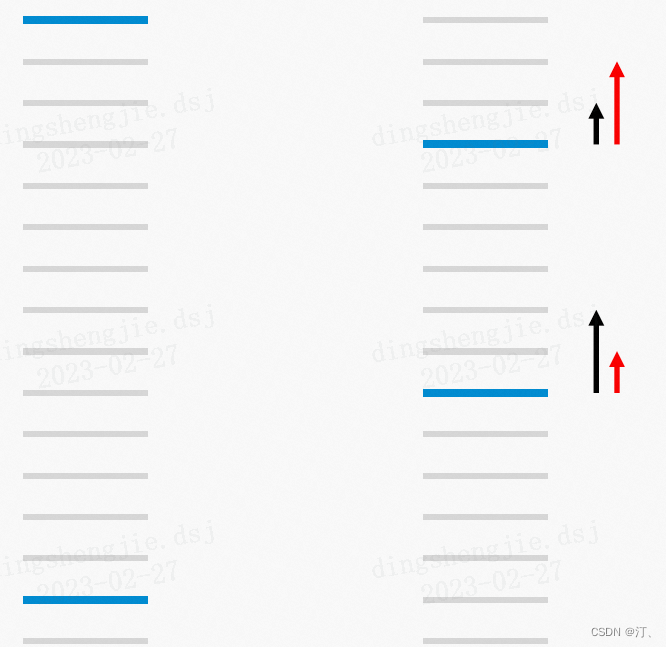
给定一个query，上图为排序结果展示，其中蓝色的线表示的是相关的文档，灰色的线表示不相关的文档，那么在左图，有13个pair对错误，而在右图中，有11个pair对错误，在RankNet，右图的排序结果要比左图好，但是在信息检索指标中，比如NDCG指标，左图的效果比右边更好。
我们在上面介绍RankNet中，将上述(1)(2)公式代人到(3)公式中，我们可以得到损失函数如下：

$\mathrm{C}=\frac{1}{2}\left(1-\mathrm{S}_{\mathrm{ij}}\right) \sigma\left(\mathrm{s}_{\mathrm{i}}-\mathrm{s}_{\mathrm{j}}\right)+\log \left(1+\mathrm{e}^{-\sigma\left(\mathrm{s}_{\mathrm{i}}-\mathrm{s}_{\mathrm{j}}\right)}\right)$

详细内容不展开参考博客：https://blog.csdn.net/BGoodHabit/article/details/122382750
4.1.1节

LambdaMART

参考上述博客4.1.2节

2. 非直接基于评价指标的算法(定义损失函数)
   这里，不再使用和评价指标相关的 loss 来优化模型，而是设计能衡量模型输出与真实排列之间差异的 loss，如此获得的模型在评价指标上也能获得不错的性能。
   经典的如 ，ListNet，ListMLE，StructRank，BoltzRank。

ListNet
ListNet与RankNet很相似，RankNet是用pair对文本排序顺序进行模型训练，而ListNet用的是整个list文本排序顺序进行模型训练。若训练样本中有m个query，假如对应需要排序的最多文本数量为n ，则RankNet的复杂度为 $O(m \cdot n^2)$而ListNet的复杂度为 $O(m \cdot n)$，所以整体来说在训练过程中ListNet相比RankNet更高效。

ListMLE
ListMLE也是基于list计算损失函数，论文对learning to rank算法从函数凸性，连续性，鲁棒性等多个维度进行了分析，提出了一种基于最大似然loss的listwise排序算法，取名为ListMLE。

上述参考博客：4.2.2节

2.3.2 Listwise细则

更多内容参考(https://blog.csdn.net/sinat_39620217/article/details/129057635)[https://blog.csdn.net/sinat_39620217/article/details/129057635]

2.3.3 Listwise排序学习（列表法）总结：

1. 它是将每个Query对应的所有搜索结果列表作为一个训练样例
2. 根据训练样例训练得到最优评分函数F，对应新的查询，评分F对每个文档打分，然后根据得分由高到低排序，即为最终的排序结果
3. 直接考虑整体序列，针对Ranking评价指标（比如MAP, NDCG）进行优化
4. 主要算法：ListNet, AdaRank，SoftRank，LambdaRank, LambdaMART等LambdaMART是对RankNet和LambdaRank的改进，在 Yahoo Learning to Rank Challenge比赛中的冠军模型

listwise 类相较 pointwise、pairwise 对 ranking 的 model 更自然，解决了 ranking 应该基于 query 和 position 问题。

listwise 类存在的主要缺陷是：一些 ranking 算法需要基于排列来计算 loss，从而使得训练复杂度较高，如 ListNet和 BoltzRank。此外，位置信息并没有在 loss 中得到充分利用，可以考虑在 ListNet 和 ListMLE 的 loss 中引入位置折扣因子。

2.4 三类方法代表汇总

wiki有很全的三类方法代表：

2019	FastAP [30]	listwise	Optimizes Average Precision to learn deep embeddings
2019	Mulberry	listwise & hybrid	Learns ranking policies maximizing multiple metrics across the entire dataset
2019	DirectRanker	pairwise	Generalisation of the RankNet architecture
2019	GSF [31]	listwise	A permutation-invariant multi-variate ranking function that encodes and ranks items with groupwise scoring functions built with deep neural networks.
2020	RaMBO[32]	listwise	Optimizes rank-based metrics using blackbox backpropagation[33]
2020	PRM [34]	pairwise	Transformer network encoding both the dependencies among items and the interactions
between the user and items

2020	SetRank [35]	listwise	A permutation-invariant multi-variate ranking function that encodes and ranks items with self-attention networks.
2021	PiRank [36]	listwise	Differentiable surrogates for ranking able to exactly recover the desired metrics and scales favourably to large list sizes, significantly improving internet-scale benchmarks.
2022	SAS-Rank	listwise	Combining Simulated Annealing with Evolutionary Strategy for implicit and explicit learning to rank from relevance labels
2022	VNS-Rank	listwise	Variable Neighborhood Search in 2 Novel Methodologies in AI for Learning to Rank
2022	VNA-Rank	listwise	Combining Simulated Annealing with Variable Neighbourhood Search for Learning to Rank

2.5 评估指标

更多内容参考(https://blog.csdn.net/sinat_39620217/article/details/129057635)[https://blog.csdn.net/sinat_39620217/article/details/129057635]

2.5.1 WTA(Winners take all)

2.5.2 MRR(Mean Reciprocal Rank)

2.5.3 RC(Rank Correlation)

2.5.4 MAP(Mean Average Precision)

2.5.5 NDCG(Normalized Discounted Cumulative Gain)

2.5.6 小结

可以发现，这些评估指标具备两大特性：

• 基于 query ，即不管一个 query 对应的 docs 排序有多糟糕，也不会严重影响整体的评价过程，因为每组 query-docs 对平均指标都是相同的贡献。
• 基于 position ，即显式的利用了排序列表中的位置信息，这个特性的副作用就是上述指标是离散不可微的。
  一方面，这些指标离散不可微，从而没法应用到某些学习算法模型上；另一方面，这些评估指标较为权威，通常用来评估基于各类方式训练出来的 ranking 模型。因此，即使某些模型提出新颖的损失函数构造方式，也要受这些指标启发，符合上述两个特性才可以。

3.推荐参考链接