给定n个元素，找出元素中的第二大元素。该问题如果用线性扫描的方法，首先找出最大值，比较n-1次；然后从n-1个元素中找出最大值即为n个元素的第二大元素，线性扫描比较n-2次，所以找到n个元素的第二大元素需要比较2n-3次。下面考虑设计一个选第二大元素的分治算法。

01、问题分析——分与治的方法

(1) 分解：将n个元素从中间一分为二，当n为奇数时，两个子问题的规模大致相等；当n为偶数时，两个子问题的规模完全相等，均为n/2。

(2) 治理：递归两个子问题，分别求出两个子问题的最大值，同时将被淘汰的较小元素记录在较大元素的列表中。比较子问题的最大值，取较大元素为原问题的最大值。最后在最大值淘汰的元素列表中找出最大值即为原问题的第二大元素。

如找10个元素6,12,3,7,2,18,90,87,54,23的第二大元素。

首先从中间一分为二，递归找出左半部分的最大值，递归找出右半部分的最大值，同时将被淘汰的较小元素记录在淘汰它的元素列表中，如图1所示。

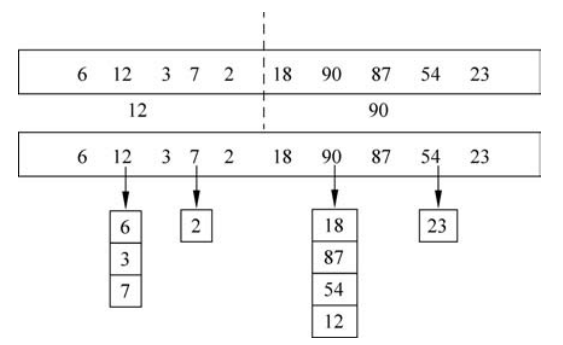
■ 图1 分解及淘汰元素列表示意

比较左半部分的最大值和右半部分的最大值，取较大者作为整个问题的最大值，即90。最后在最大值90的淘汰元素列表中找最大值，即87，即为整个问题的第二大元素。

02、算法设计

1●设计思想

通过问题分析，n个元素存储在列表a_list中，令left表示子问题的下边界，right表示子问题的上边界，则a_list［left:right］表示不同的子问题。其分解步骤表示为mid = (left+right)/2；递归的边界条件表示为left≥right，当问题规模为1时，单个元素本身就是序列的最大值。

治理划分为两个阶段：
①递归求解a_list［left:mid］和a_list［mid+1:right］两个子问题的最大值left_max和right_max，同时将被淘汰的元素放入淘汰它的元素对应的列表中。比较left_max和right_max，取较大的作为n个元素的最大值。
②在n个元素的最大值淘汰的元素列表中，顺序查找最大值，即为第二大元素。

2●伪码描述

第一个阶段找n个元素的最大值，伪码描述如下：