增广路算法

定理4(增广路定理)设flow是网络G的一个可行流，如果不存在从源点s到汇点t关于flow的可增广路P，则flow是G的一个最大流。

1●增广路算法思想

增广路算法是由Ford和Fulkerson于1957年提出的。该算法寻求网络中最大流的基本思想是寻找可增广路，使网络的流量得到增加，直到最大为止。即首先给出一个初始可行流，这样的可行流是存在的，例如零流。如果存在关于它的可增广路，那么调整该路上每条弧上的流量，就可以得到新的可行流。对于新的可行流，如果仍存在可增广路，则用同样的方法使流的值增大。继续这个过程，直到网络中不存在关于新的可行流的可增广路为止。此时，网络中的可行流就是所求的最大流。

该算法分以下两个过程：

(1) 找可增广路。

可采用标号法找可增广路。对网络中的每个节点j，其标号包括两部分信息(pred(j)，maxl(j))。其中，pred(j)表示节点j在可能的增广路中的前一个节点；maxl(j)表示沿该可能的增广路到节点j为止可以增加的最大流量。

具体步骤如下：

第一步，源点s的标号为(0，+∞)。

第二步，从已标号而未检查的点v出发，对于边，如果flow(v，w)<cap(v，w)，则w的标号为(v，maxl(w))，maxl(w)=min{maxl(v),cap(v，w)-flow(v，w)}；对于边，flow(w，v)>0，则w的标号为(-v，maxl(w))，maxl(w)=min{maxl(v)，flow(w，v)}。

第三步，不断重复步骤2，直到已经不存在已标号未检查的点或标到了汇点结束。如果不存在已标号未检查的点，就说明不存在关于当前可行流的可增广路，当前流就是最大流。如果标到了汇点，就找到了一条可增广路，需要沿着该可增广路进行增流，转过程(2)。

(2) 沿着可增广路进行增流。增流方法为：

先确定增流量d，即d=maxl(t)，然后依据下面的公式进行增流。

增流以后的网络流依旧是可行流。

2●算法设计

采用队列LIST来存放已标号未检查的节点。根据增广路算法的思想，算法设计如下：

第一步，初始化可行流flow为零流；对节点t标号，即令maxl(t)=任意正值(如5)。

第二步，若maxl(t)>0，继续下一步；否则算法结束，此时已经得到最大流。

第三步，取消所有节点j∈V的标号，令maxl(j)=0，pred(j)=0；令LIST={s}，对节点s标号，令maxl(s)=∞。

第四步，如果LIST≠∮，且maxl(t)=0，继续下一步；否则：

(1) 如果t已经有标号(即maxl(t)>0)，就找到了一条增广路，沿该增广路对流flow进行增流(增流的流量为maxl(t)，增广路可以根据pred回溯方便得到)，转第二步。

(2) 如果t没有标号(即LIST=∮且maxl(t)=0)，那么转第二步。

第五步，从LIST中移走一个节点i，寻找从节点i出发的所有可能的增广边。

(1) 对非饱和的向前边，若节点j没有标号，则对j进行标号，即令maxl(j)=min{maxl(i)，cap(i，j)-flow(i，j)}，pred(j)=i，并将j加入LIST中，转第四步。

(2) 对非零向后边，若节点j没有标号，则对j进行标号，即令maxl(j)=min{maxl(i), flow(i，j)}，pred(j)=-i，并将j加入LIST中，转第四步。

3●增广路算法的构造实例

【例1】用增广路算法找出如图1所示的网络及可行流的最大流，其中，顶点1为源点，顶点6为汇点，边上的权为(cap，flow)。

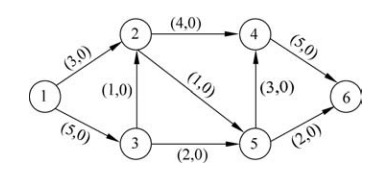
图1网络及可行流

解：标号法找增广路(按顶点序号由小到大的顺序选择已标号未检查的点)如图2所示（注：增广路在图中用黑粗线表示）。

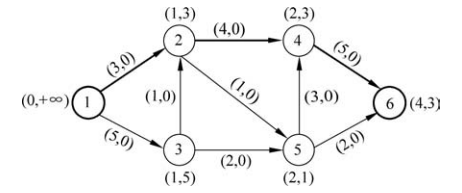
图2 第一次找到的一条可增广路

沿着增广路增流，增加的流量d=3。增流后得到的新的可行流如图3所示。

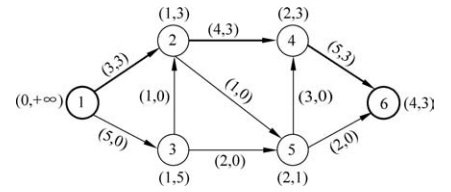
图3第一次增流后的可行流

根据增广路算法，取消所有顶点的标号，给它们重新标号，如图4所示。

图4第二次找到的可增广路

沿着增广路增流，增加的流量d=2。增流后的可行流如图5所示。

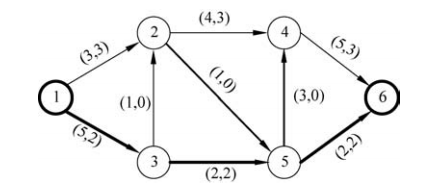
图5第二次增流后的可行流

根据增广路算法，取消所有顶点的标号，给它们重新标号，如图6所示。

图6第三次找到的可增广路

沿着增广路增流，增加的流量d=1，增流后的可行流如图7所示。

图7第三次增流后的可行流

重新开始标号，标号过程进行到3号顶点后无法继续进行，当前网络中已没有关于当前可行流的可增广路，该可行流已达到了最大流，如图8所示。

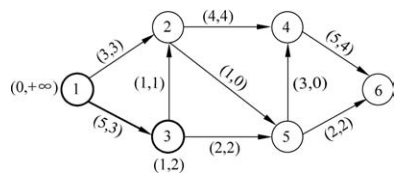
图8网络最大流