Dijistra算法（最短路径）

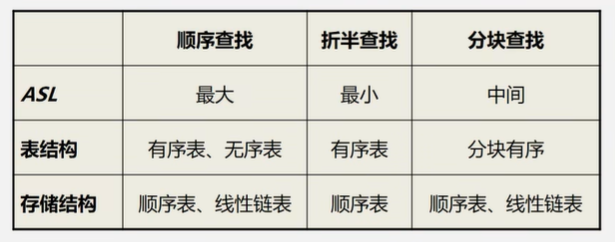
折半查找

适用于有序表

分块查找

①建立索引表，分块记录每一块的最大值

②在索引表中查找，确定是在哪一块

③块内进行顺序查找

平均查找长度：ASL=Lb+Lw（索引表+块内）

Lb = log2(n+1)（n：s总元素/每一块的元素 = 块）

Lw = (s/2)（s：总元素）

树表的查找

二叉排序树

左子树小于根、右子树大于等于根

中序遍历是递增有序的序列

递归查找

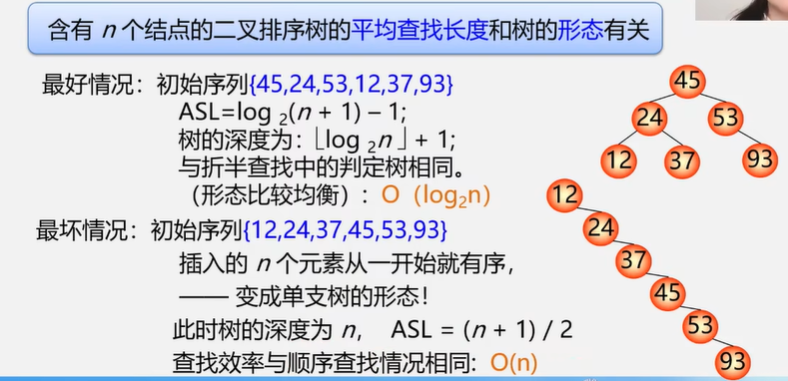
最多比较次数：数的深度

平均查找长度：和数的形态有关，O(log2n)

二叉排序树插入：都在叶结点上，修改指针，不需要移动元素

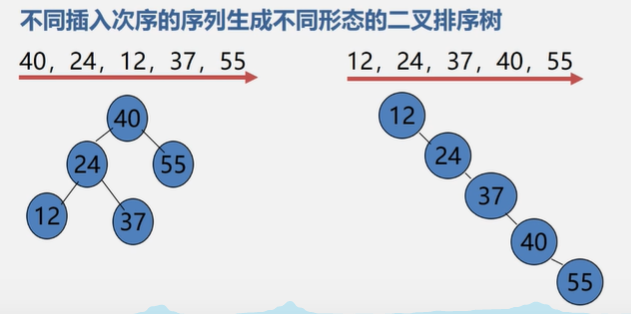
二叉排序树生成：依次插入，重复元素不插入

输入序列不同，生成的二叉树不一样，查找效率也不一样

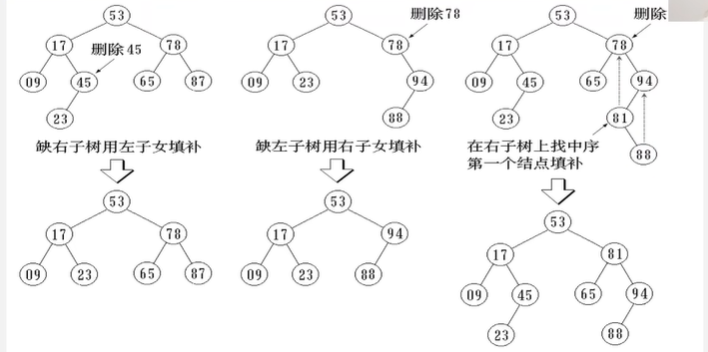
二叉排序树删除：

• 删除的结点是叶子结点：直接删掉就行
• 删除的结点是根结点：如果只存在左孩子或者右孩子，就用孩子替换它；
• 删除的结点有两个孩子的结点：
• 右子树中的最小的结点代替这个被删的结点，将右子树中最小的结点删除；
• 左子树中找到最大的结点，并删除这个结点，将这个结点的值放在被删的结点里面

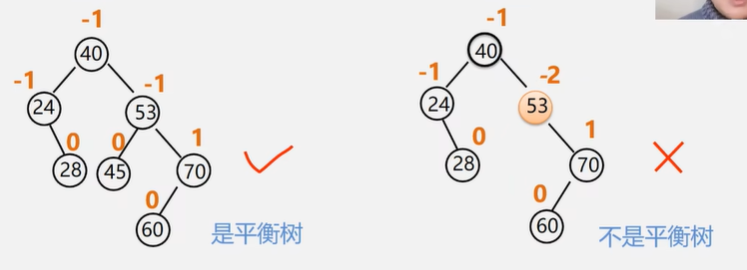
平衡二叉树（AVL）

平衡因子：左子树与右子树的高度差

BF = 结点左子树的高度 - 结点右子树的高度

BF = -1、0、1（就是平衡二叉树）

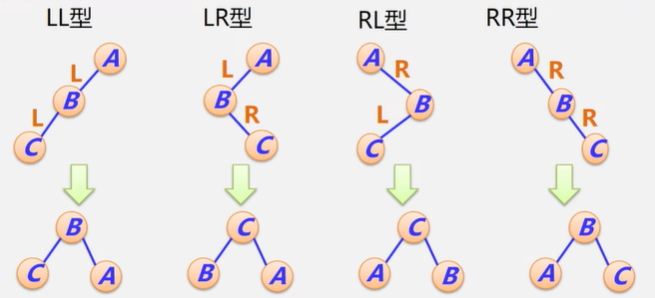
失衡二叉树的分析与调整（四种类型）

LL型、LR型、RL型、RR型

①降低树的高度

②保持二叉排序树的性质（左<根<右）

1. LL型
2. B结点带左子树C一起上升
3. A结点成为B的右孩子
4. 原来的B结点的右子树作为A的左子树

散列表

基本思想：记录的存储位置与关键字之间存在的对应关系

hash函数

看下面这个散列表：

根据散列函数来查找：H(key) = k

优点：查找效率高

缺点：空间效率低

例如：H(k) = k mod n（n：元素个数+1）

冲突：k1≠k2 但是H(k2)=H(k2)

减少冲突：优化散列函数

散列函数的构造方法需要考虑的问题：

1. 执行速度
2. 关键字的长度
3. 散列表的大小
4. 关键字的分布情况
5. 查找频率

直接定值法：关键字构成某种线性函数

解决冲突：如果找到的地址已经存储了值了，就移动到下一个地址

解决冲突的方法：

除留余数法：Hi = (Hash(key)+di) mod m（di为增量序列）

1. 线性探测法：di为1，2，...m-1
2. 二次探测法：di为1^2，-1^2，2^2，-2^2，...，q^2
3. 伪随机探测法：di为伪随机数序列

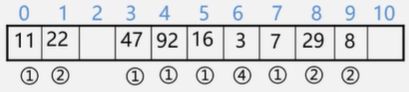
例如：{47,7,29,11,16,92,22,8,3}【线性探测法】

m=11 散列函数为：Hash(key) = key mod 11

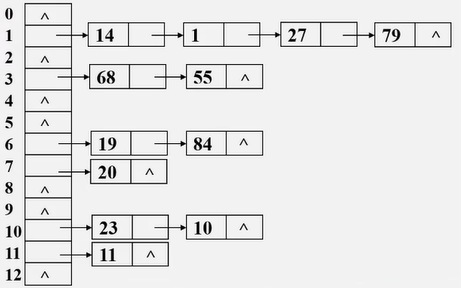
链地址法：余数相同的链接在一个单链表上（头插法）

例如：{19,14,23,1,68,20,84,27,55,11,10,79}

优点：非同义词不会冲突，无聚集现象；适用表长不确定。

散列表的查找ASL：每个元素查找的次数之和 / 元素总个数

排序

排序方法的分类

1. 存储介质：内部排序（内存）、外部排序（内+外）
2. 比较器个数：串行排序（单处理）、并行排序（多）
3. 主要操作：比较排序（插入、交换、选择、归并）、基数排序
4. 辅助空间：原地排序（不需要额外的空间）、非原地排序（需要辅助空间）
5. 稳定性：稳定排序（直接插入排序，相等元素排序后不变）、非稳定排序（简单选择排序，相等元素排序后改变）
6. 自然性：自然排序（有序快）、非自然排序（有序慢）

按排序依据原则

1. 插入排序：直接插入排序(顺序)、折半插入排序(二分)、希尔排序(缩小增量)
2. 交换排序：冒泡排序、快速排序
3. 选择排序：简单选择排序、堆排序
4. 归并排序：2-路归并排序
5. 基数排序

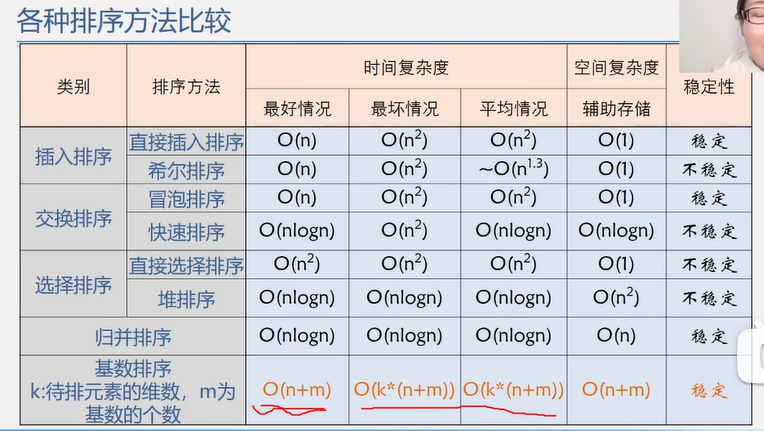
排序算法的好坏

1. 时间效率
2. 空间效率
3. 稳定性

插入排序

插入排序：在有序序列中插入一个元素，保持序列有序

1.直接插入排序：顺序查找插入的位置，还可以使用哨兵模式

算法效率：比较+移动

2. 二分插入排序：查找插入位置时采用折半查找法，使用哨兵。

3. 希尔排序：分割若干个子序列，分别进行直接插入排序；定义递减的增量序列，比如5、3、1，最后一个增量必须为1

交换排序

交换排序：两两比较，如果发生逆序就交换

1.冒泡排序：每一趟不断将记录两两比较，并按“前小后大”规则交换

2.快速排序：任取一个元素为中心，所有比它小的元素一律前放，比它大的元素一律后放，形成左右子表（交替式逼近法，递归）；

选择排序

1.简单选择排序：在等待排序的数据中选出最大(小)的元素放在其最终位置。

例如：直接选出最小的 放在第一个位置

2.堆排序：

小根堆：根都小于等于左右结点

大根堆：根都大于等于左右结点

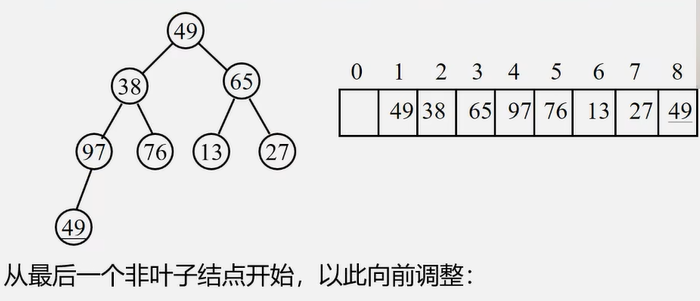
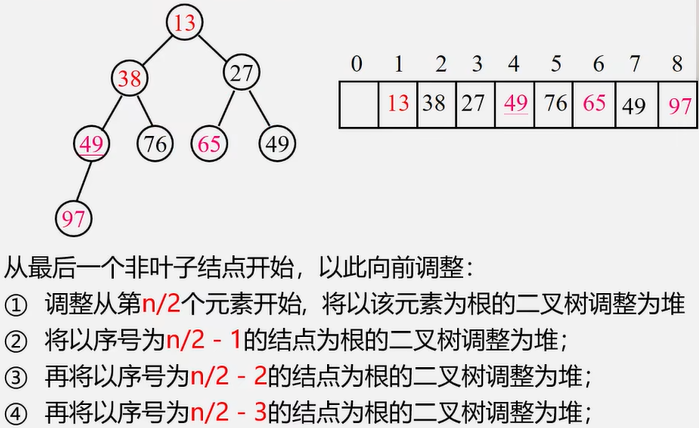
完全二叉树的非叶子结点（位置i）：i > n/2

无序序列建立成一个堆： 将元素直接排成堆 然后再调整

归并排序

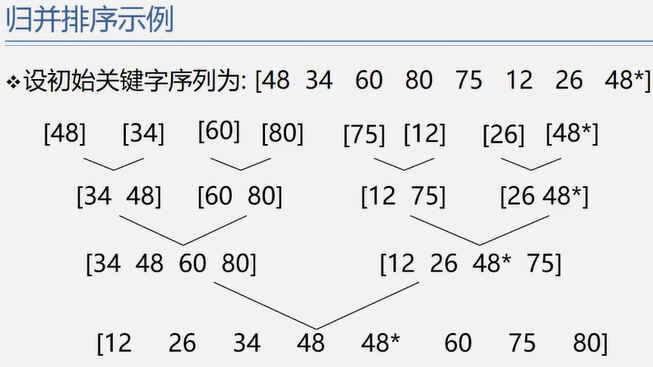
归并排序：将两个或者两个以上的有序序列“归并”为一个有序序列。

1.二路归并排序

排序完成需要log2n次。

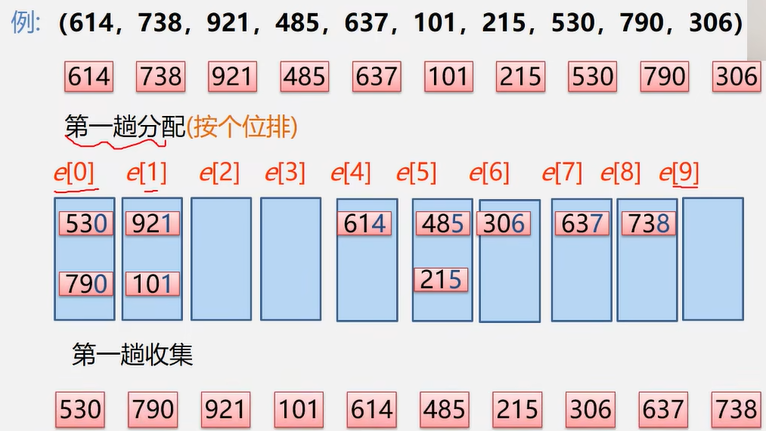
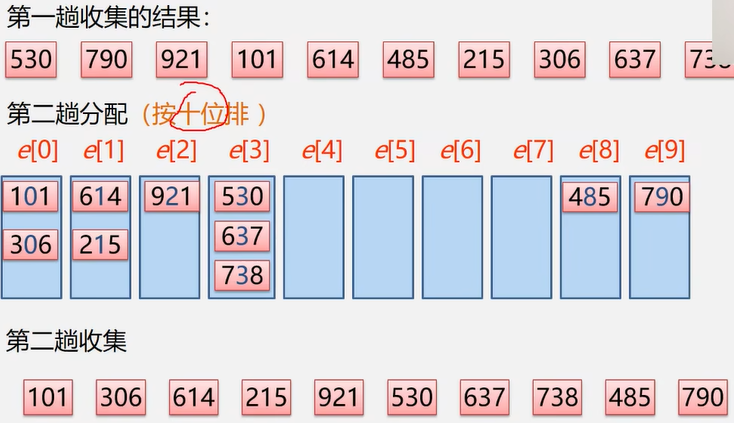
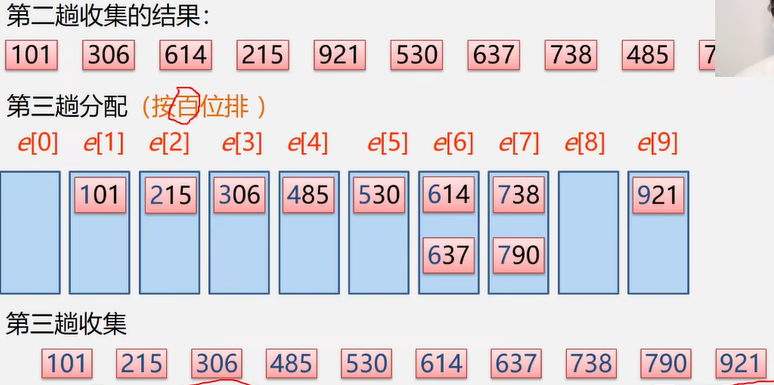
基数排序

1. 基数排序：分配+收集

排序总结