第十四届蓝桥杯集训——练习解题阶段(无序阶段)-分治算法

​

 ​编辑

第十四届蓝桥杯集训——练习解题阶段(无序阶段)-分治算法

分治算法

百度词条解释：

        分治算法的基本思想是将一个规模为N的问题分解为K个规模较小的子问题，这些子问题相互独立且与原问题性质相同。求出子问题的解，就可得到原问题的解。即一种分目标完成程序算法，简单问题可用二分法完成。

基本思想：

        当我们求解某些问题时，由于这些问题要处理的数据相当多，或求解过程相当复杂，使得直接求解法在时间上相当长，或者根本无法直接求出。对于这类问题，我们往往先把它分解成几个子问题，找到求出这几个子问题的解法后，再找到合适的方法，把它们组合成求整个问题的解法。如果这些子问题还较大，难以解决，可以再把它们分成几个更小的子问题，以此类推，直至可以直接求出解为止。这就是分治策略的基本思想。

最简单的分治算法——二分法

        利用分治策略求解时，所需时间取决于分解后子问题的个数、子问题的规模大小等因素，而二分法，由于其划分的简单和均匀的特点，是经常采用的一种有效的方法，例如二分法检索。

解题步骤

（1）分解，将要解决的问题划分成若干规模较小的同类问题；
（2）求解，当子问题划分得足够小时，用较简单的方法解决；
（3）合并，按原问题的要求，将子问题的解逐层合并构成原问题的解。

分治算法例题：

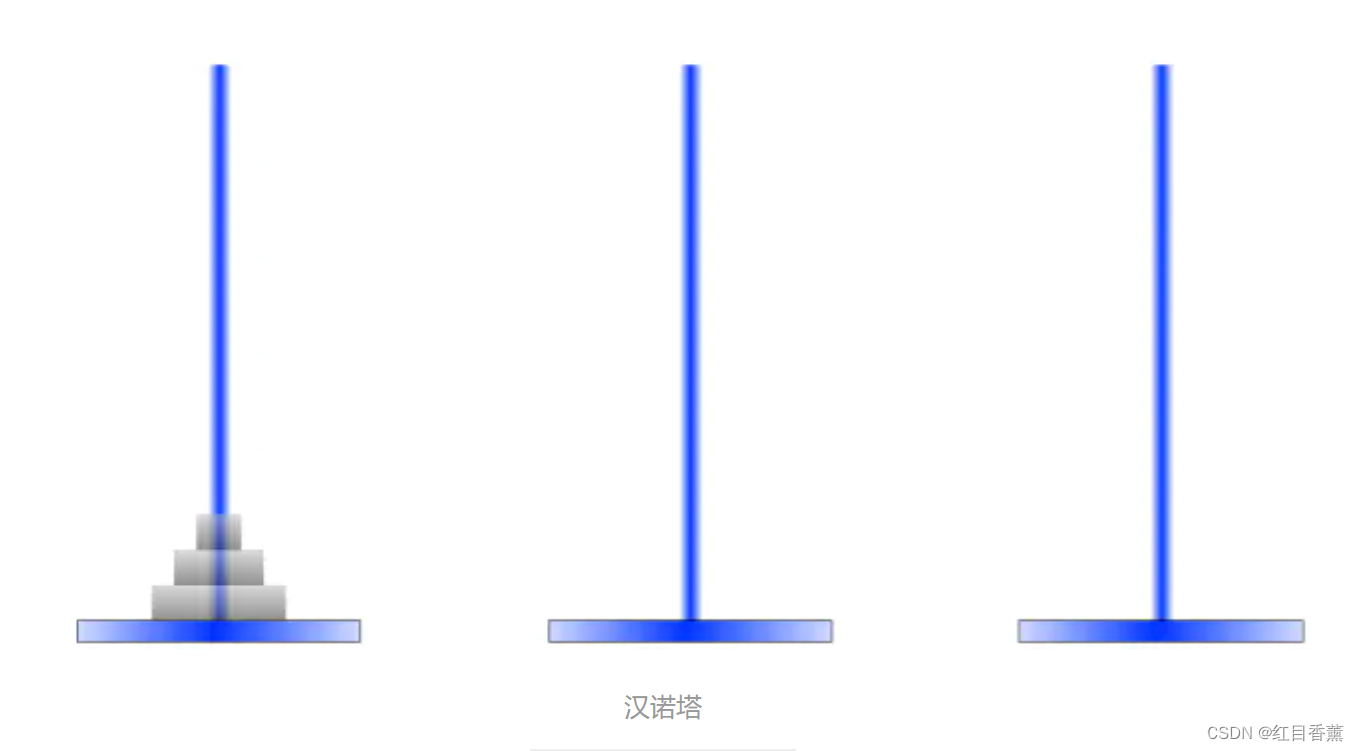
汉诺塔

​编辑

        汉诺塔（又称河内塔）问题是源于印度一个古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子，在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定，在小圆盘上不能放大圆盘，在三根柱子之间一次只能移动一个圆盘。

​编辑

package com.item.action;

public class Demo5 {

	public static void main(String[] args) {
		hanoiTower(6, "A", "B", "C");
	}

	/**
	 * 汉诺塔问题
	 * 
	 * @param plateNum 盘子的数量
	 * @param a        出发地，初始的时候是A
	 * @param b        中转地，初始的时候是B
	 * @param c        目的地，初始的时候是C
	 */
	public static void hanoiTower(int plateNum, String a, String b, String c) {
		if (plateNum == 1) {
			System.out.println("从 " + a + " 到 " + c);
		} else { // 盘子数量大于等于2的情况
			// 上面的从A到B
			hanoiTower(plateNum - 1, a, c, b);
			// 最下面那个从A到C
			System.out.println("从 " + a + " 到 " + c);
			// B针上的所有搬到C
			hanoiTower(plateNum - 1, b, a, c);
		}
	}

}

移动过程

​编辑

应用场景

运用分治策略解决的问题一般来说具有以下特点：

1、原问题可以分解为多个子问题

这些子问题与原问题相比，只是问题的规模有所降低，其结构和求解方法与原问题相同或相似。

2、原问题在分解过程中，递归地求解子问题

由于递归都必须有一个终止条件，因此，当分解后的子问题规模足够小时，应能够直接求解。

3、在求解并得到各个子问题的解后

应能够采用某种方式、方法合并或构造出原问题的解。

总结

不难发现，在分治策略中，由于子问题与原问题在结构和解法上的相似性，用分治方法解决的问题，大都采用了递归的形式。在各种排序方法中，如归并排序、堆排序、快速排序等，都存在有分治的思想。

​