DH算法 | Diffie-Hellman 密钥交换
概述:
DH 算法又称“Diffie–Hellman 算法”,像往常的算法名字一样,这是用俩个数学牛人的名字来命名的算法,实现安全的密钥交换,通讯双方在完全没有对方任何预先信息的条件下通过不安全信道创建起一个密钥。
优点:
- 通讯双方事先不需要有共享的秘密。
- 用该算法协商密码,即使中间被截获,也无法解密出来密钥是啥
缺点:
- 没有办法进行认证
- 计算很复杂,但是一般情况下,一个会话只用计算一次,那么假如有大量的请求,就会耗费大量的资源来进行计算,容易受阻塞性攻击
- 其余的缺点,感兴趣的可以自行百度(QAQ)
数学理论支撑
从概念上讲,要想破解DH算法,那么就是在求解离散对数问题,
离散对数难题是指:当已知一个大质数p和它的一个原根a,如果给定一个b,要计算i的值是相当困难的。
是一个典型的正向求解简单,逆向求解特别难的问题
举例:
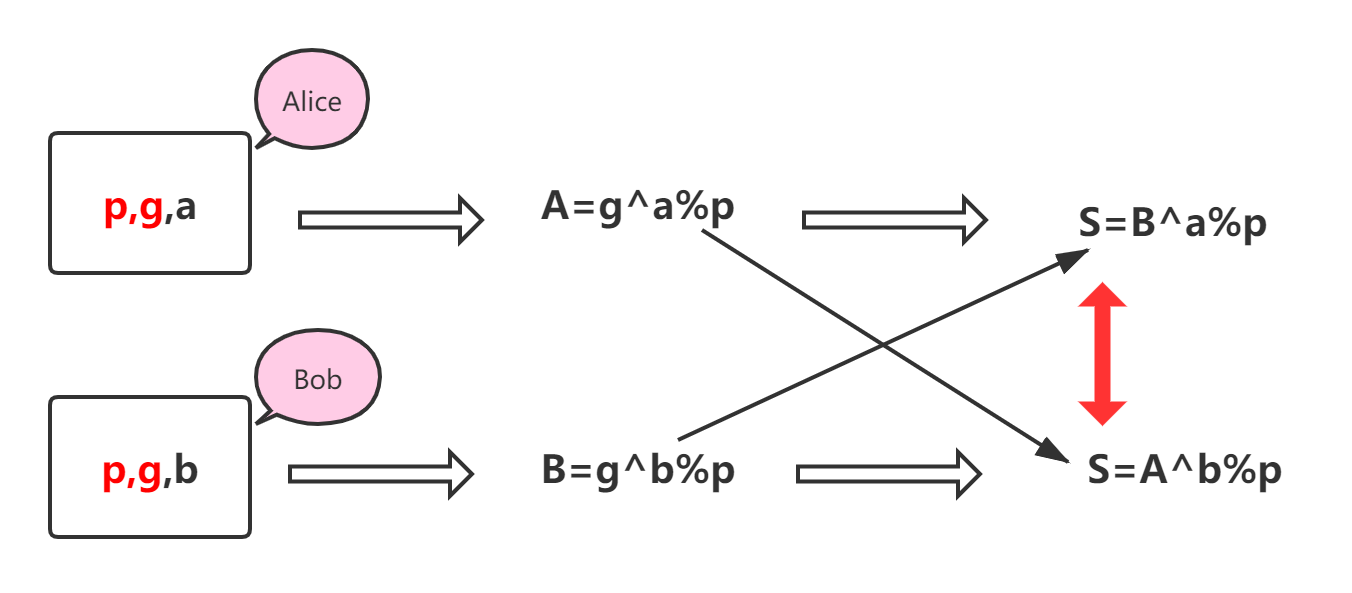
通讯双方(张三、李四)需要先约定好算法参数(algorithm parameters):一个素数 p 作为模数,一个素数 g 作为基数(g 也称为“生成元”)。这两个算法参数是可以对外公开滴。
对于张三而言,需要先想好一个秘密的自然数 a 作为私钥(不能公开),然后计算 A = ga mod p 作为自己的公钥(可以公开)。
对李四而言也类似,先想好一个秘密的自然数 b 作为私钥(不能公开),然后计算 B = gb mod p 作为自己的公钥(可以公开)。
张三和李四互相交换各自的公钥。
然后张三计算出 k = Ba mod p,李四计算出 k = Ab mod p
我们不难发现,张三和李四最后计算出来的k必然是一致的
他们都无法通过已知 的数来推算出对方的私钥
对于中间截获者来说,虽然能看到 p,g,A,B,但是无法推算出 a 和 b(就是说,旁观者无法推算出双方的私钥),自然也无法推算出 k
DH算法
算法核心:为了生成一个共享的秘密——密钥
算法步骤:
-
客户端随机生成随机值Ra
计算Pa(x, y) = Ra * Q(x, y),
Q(x, y)为全世界公认的某个椭圆曲线算法的基点
将Pa(x, y)发送至服务器 -
服务器随机生成随机值Rb
计算Pb(x,y) = Rb * Q(x, y)
将Pb(x,y)发送至客户端 -
客户端计算Sa(x,y) = Ra * Pb(x,y)
服务器计算Sb(x,y) = Rb *Pa(x,y) -
算法保证了Sa = Sb = S,提取其中的S的x向量作为密钥(预主密钥)
- 点赞
- 收藏
- 关注作者


评论(0)