@TOC

一、题目描述

原题传送门

示例 1：

输入：head = [[7,null],[13,0],[11,4],[10,2],[1,0]]
输出：[[7,null],[13,0],[11,4],[10,2],[1,0]]

示例 2：

输入：head = [[1,1],[2,1]]
输出：[[1,1],[2,1]]

示例 3：

输入：head = [[3,null],[3,0],[3,null]]
输出：[[3,null],[3,0],[3,null]]

提示：

• 0 <= n <= 1000
• -104 <= Node.val <= 104
• Node.random 为 null 或指向链表中的节点。

此题是力扣上一道==中等难度==的题目，不过相信很多同学在看了这道题目之后都点云里雾里的感觉，觉得这道题很复杂的样子，一个链表有两个指针域，而且有一个还是随机指针，对于题目的描述完全不读懂它在讲点什么。

是的，这道题虽说是中等难度的题目，但是在我看来本题算是链表章节的题目中比较综合的题，虽然它没有【环形链表】那么绕，需要一些数学的思维，但它的结构是比较复杂的，需要做题者对于链表的掌握程度达到一定的水准，不然得话在处理其指针的关系时就会思绪混乱、无从下手

二、思路分析与罗列

思路一：通过原链表的【random】去找控制拷贝链表的【random】

• 首先来理一下这个题目的思路，其实把这就是一个单链表，只是它存在一个随机指针罢了，那题目的意思就是复制每一个结点，而且复制出来的结点不可以指向原链表中的结点，也就是要重新修改指向，对于这个【random】指针也需要有一个复制。那其实可以看到，就是==完整地将这个链表复制一份出来==

• 那有同学就说，这不是很简单，把每一个结点做一个拷贝，然后再将它们做一个链接，之后再将【random】指针也做一个相同的指向不就好了。【next】指针确实可以做一个链接，但是你觉得这个【random】指针也可以直接这样做一个链接吗？

• 就好比这里的【13】，原链表中是指向7，现在可以指向7,；对于【11】，原链表是指向1，那是在下午我做了一个修改后，现在有两个1了，那指向哪个呢？一般来说都是默认前面那个，因为单链表只能从前往后遍历，那算你能从后往前遍历，【1】是指向【7】的，但是后面又出现一个【7】怎么办呢，那又会出现混乱。所以我们不可以直接指向其原来的位置，要指向哪里？–》==相对位置==

• 这个时候我们就需要去找到这个相对位置，不是去找你【random】值向的值是第几个，而是寻找【random】指向的那个地址，根据地址去进行一个查找。也就是通过原链表的【random】去控制拷贝链表的【random】
• 首先看到【7】，原链表的【random】指向【NULL】，那拷贝链表也就指向它这里的【NULL】，根据【copy】和【cur】当前所指的值进行一个对比
• 此时我们需要定义一个变量【i】去寻找当前原链表【cur】的【random】所指向的地址，那此时这个【i】就需要一直去遍历，找到原链表中的【NULL】

• 此时就需要这个【i】去遍历这个链表进行查找，【i++】就会加到5，此时拷贝链表只需要进行一个【while(i–)】，就可以找到它那里的这个【NULL】了

• 然后【cur】和【copy】后移继续更新【random】，但是【i】不需要动，此时原链表中的【1】指向位置为0的【7】，因此拷贝链表也指向位置为0的【7】

• 然后继续进行一个迭代，此时原链表中的【11】指向的是后面的那个【1】，于是下标【i】就开始寻找指向的那个地址

• 然后【i】去寻找，找一个【++i】，找一个【++i】，==直到找到原链表的这个结点的【random】指向的地址为止==

• 然后拷贝链表也需要做这么一个修改，后面的也是类似，便不细讲

• 我们来分析一下思路，大家认为这个思路的【时间复杂度】是多少，我们知道，时间复杂度是要算最坏的，那我举一个例子，例如说这个【7】，它是指向【NULL】的，然后这个【1】和【11】，我现在做一个修改，让它们也去指向这个【NULL】，那此时这个原链表和拷贝链表都需要遍历【N】次才可以找到这个位置，所以时间复杂度很可能到达O(N^2^)
• 那O(N^2^)这个时间复杂度是不是太高了，于是我们就需要开始思考有没有O(N)的思路可以实现的，你能想到到吗？接下来我们再来讲一种思路

---

思路二：直接链接到原链表处做相邻结点的【random】修改

先行说明，这种思路的时间复杂度是O(3N)，最后进行大O渐进法的优化就是==O(N)==

• 好，接下去我们就来讲讲这种思路，它一共分为三步

Step1：把复制的结点插入到原结点后

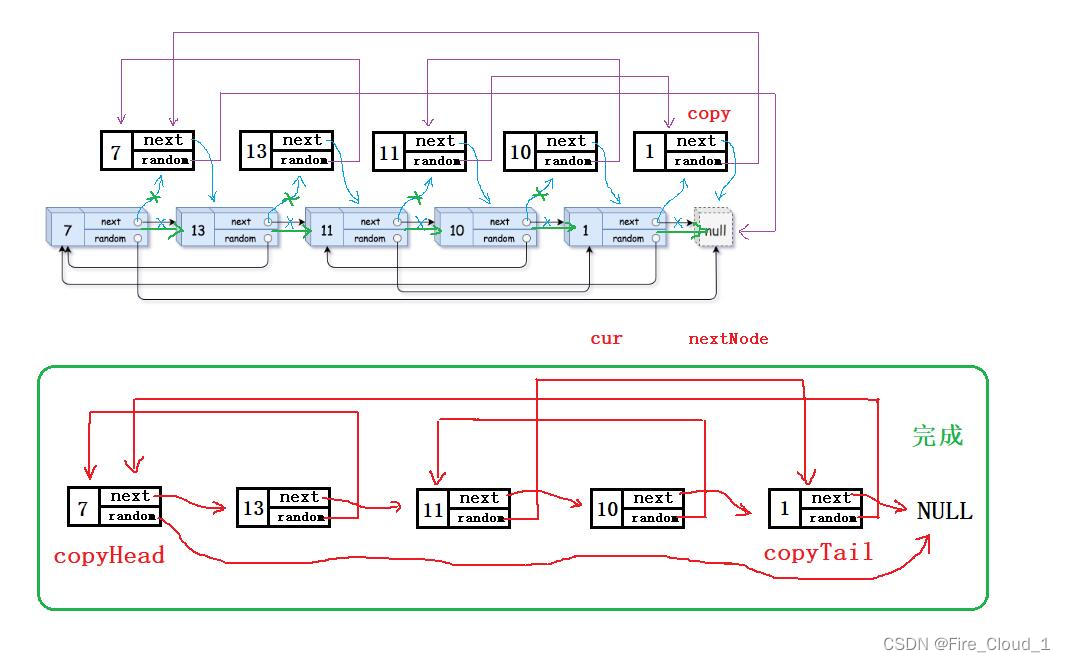
• 首先是第一步，从下图可以看到，我们定义一个【cur】指向原链表的结点，然后根据这个结点去【malloc】出一个新的结点，之后让他们的【val】值都相同
• 接下去我们要修改的就是【next】指针域，这个很容易，保存一下当前【cur】结点的下一个结点，然后将【copy】结点和它们进行一个互连即可，链接好后做一个迭代更新

• 展示一下核心代码

Node* cur = head;
while(cur)
{
    Node* copy = (Node *)malloc(sizeof(Node));
    copy->val = cur->val;

    //插入结点
    Node* nextNode = cur->next;
    cur->next = copy;
    copy->next = nextNode;

    //迭代
    cur = nextNode;
}

Step2：设置拷贝结点的random值【⭐⭐⭐】

• 好，接下去我们开始做第二步，就是去设置每个【copy】结点的【random】指针指向。这一步非常得关键::key:也是比较难理解的一趴，所以要专注精神哦
• 首先第一个【7】，它的【random】是指向【NULL】，所以当前【copy】的【random】也要指向【NULL】，这个我们需要单独做判断

• 然后对于【13】，我们是不是要让它指向【copy】的【7】，但是要怎么找到它呢？此时我们需要根据当前的【cur】，也就是原链表中当前结点的【random】所指向结点的【next】，去寻找这个拷贝的【random】域
• 那有同学问，为什么可以这么找呢？这是由什么依据吗？因为我们刚才是将每一个拷贝结点都链接到了源结点之后，所以通过找到源节点的【random】域，找它的【next】，就可以很轻松地寻找到拷贝结点的【random】域

我们继续看下去。一样，这个【11】可以通过源节点【11】的【random】域所指向的【1】，然后去找到它后面的一个结点，然后【copy->next】等于它即可

• 同上

• 你可试着自己分析

• 给出这部分的代码

cur = head;
while(cur)
{
    Node* copy = cur->next;
    if(cur->random == NULL)
        copy->random = NULL;
    else
        //拷贝结点的随机指针即为原结点的随机指针所指向结点的下一个结点
        copy->random = cur->random->next;
    //迭代（移动两步）
    cur = copy->next;
}

• 好，到这里我们的第二步就算是完成了，这个时候其实你去力扣上提交的话已经是可以过了，但是你不觉得这样整个链表变得很冗杂吗？那要怎么对其再进行一个优化呢？

Step3：提取复制后的链表恢复原链表

• 此时我们就需要第三步，也就是将这个拷贝完后链表从原链表中分割出来，然后恢复原来链表的指向。既然我们借用了原来链表的结构，去方便地将拷贝链表的【random】域做了一个链接，那此时我们就要将其恢复
• 这其实和我们现实中的大哥带小弟一个道理，大哥把房间给到小弟一起住，然后小弟每天努力拼搏，最后有了能力，翅膀也硬了✈，要自己单飞了。但是呢，大哥先前对你这么好，你在临走前是不是要把大哥给你住的房间打扫一遍，收拾一下，这样才算样子

---

好，插了一个题外话，我们继续分析这第三个步骤

• 首先，既然是要把拷贝的每一个结点单独拿出来，那就需要将其重新构成一个链表的形式，那其实也就是我们熟悉的尾插，如下图所示

• 这里的拷贝结点的【random】域无需去理会它，只是我为了完整性而画的

• 可以看到，只需要把【copy】结点一个个拿下来，做一个尾插，然后在原链表中进行一个【三指针的迭代】即可。可能有同学会疑惑将这个结点拿下来后拷贝结点的【random】指针不会变化吗？当然不会，只要你不去修改，那它就一直是指向它之前已经指向的那块地址，
• 如果有这个疑惑的同学，你可以去仔细看看我的单链表从浅入深详解，你就会明白了

• 同上。而且还要说明一点，如果你仔细看可以发现，我对于原链表的指向也是同步地再做修改

• 可以看到，此时我们就把依附在原链表中的拷贝结点一一分解下来，然后做成了一个新的链表形式。此时只需要返回【copyHead】就可以获取整个拷贝后的链表

• 代码在下一模块统一给出。你可先根据我的推导分析自己画画图写一遍，再与我的代码进行对照

时间复杂度与空间复杂度的分析

• 第一个思路的时间复杂度说过了，是O(N^2^)，空间复杂度是O(N)
• 我们主要来分析一下第二个思路的复杂度，开头说过是O(3N)：分别分析三个步骤，可以发现他们都需要O(N)，第一个步骤是插入、第二个步骤是查找、第三个步骤是尾插，如果你认真看过我的单链表就可以知道，他们都是O(N)的复杂度，那么三个O(N)就是O(3N)，可以优化为O(N)。
• 那对于空间复杂度是多少呢？没错，也是O(N)，因为我们需要存放拷贝的结点值，就要从堆区为其开辟一块空间，使用到了【malloc】，如果复杂度这一块不是很懂的同学可以看看我的这篇文章时间与空间复杂度就看这篇了

三、整体代码展示

展示一下整体的代码，不过还是自己去敲一遍比较好哦

• 第一个思路不够优，因为不做过多分析。我们主要掌握第二个思路

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* next;
    Node* random;
    
    Node(int _val) {
        val = _val;
        next = NULL;
        random = NULL;
    }
};
*/

class Solution {
public:
    Node* copyRandomList(Node* head) {
        //1、把复制的结点插入到原结点后
        Node* cur = head;
        while(cur)
        {
            Node* copy = (Node *)malloc(sizeof(Node));
            copy->val = cur->val;

            //插入结点
            Node* nextNode = cur->next;
            cur->next = copy;
            copy->next = nextNode;

            //迭代
            cur = nextNode;
        }

        //2、设置拷贝结点的random值
        cur = head;
        while(cur)
        {
            Node* copy = cur->next;
            if(cur->random == NULL)
                copy->random = NULL;
            else
                //拷贝结点的随机指针即为原结点的随机指针所指向结点的下一个结点
                copy->random = cur->random->next;
            //迭代（移动两步）
            cur = copy->next;
        }

        //3、提取复制后的链表恢复原链表
        cur =  head;
        Node* copyHead, *copyTail;
        copyHead = copyTail = NULL;
        while(cur)
        {
            Node* copy = cur->next;
            Node* nextNode = copy->next;

            //恢复原链表的指向
            cur->next = nextNode;

            //尾插逻辑
            if(copyTail == NULL)
            {
                copyHead = copyTail = copy;
            }
            else
            {
                copyTail->next = copy;
                copyTail = copyTail->next;
            }
            cur = nextNode;
        }

        return copyHead;
    }
};

• 可以看到，这个思路的代码量确实是很大，可能你听懂了我的思路，但若是你自己去画图分析再写代码，是需要耗费一定时间的，如果你可以独立地分析写出来，说明你链表部分掌握的还算是不错了，可以进入下一关:door:

四、总结与提炼

• 最后我们来总结一下本文所介绍的内容，本文讲解的是一道力扣中有关链表章节比较综合性的题目，一共有两个思路，第一个思路的复杂度较高，不够优，因此我们了解一下即可；第二个思路的解法比较优一些，但是实现起来比较繁琐，需要你对指针这一块有着很熟练的掌握。
• 本题考察得比较综合，若是还觉得吃力的小伙伴应该再回过头去看看一些没搞懂知识点，正确做到对链表对一块能够熟练掌握，因为这是我们【数据结构】中最重要，也是最基础的一块，为后续的二叉树、红黑树、哈希表等复杂数据结构打下坚实的基础🛡

以上就是本文所要描述的所有内容，感谢您对本文的观看，如有疑问请于评论区留言或者私信我都可以:four_leaf_clover: