@toc

1、题目及实现思路

  题目：假设我们有 4 个 2 维的数据，数据的特征分别是(3,3),(4,3),(1,1),(2,1)。
  (3,3),(4,3) 这两个数据的标签为 1，
  (1,1),(2,1)这两个数据的标签为-1。
  构建神经网络来进行分类。

  思路：我们要分类的数据是 2 维数据，所以只需要 2 个输入节点（一般输入数据有几个特征，我们就设置几个输入神经元），我们可以把神经元的偏置值也设置成一个输入节点。这样我们需要 3 个输入节点。

  输入数据有 4 个(1,3,3),(1,4,3),(1,1,1),(1,2,1)

  数据对应的标签为(1,1,-1,-1)

  初始化权值 w1,w2,w3 取 0 到 1 的随机数

   学习率 lr(learning rate)设置为 0.1

  激活函数为 sign 函数

  我们可以构建一个单层感知器如图所示。

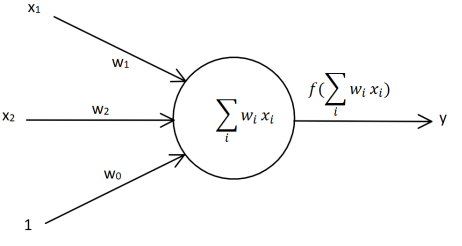
2、代码实战

import numpy as np
import matplotlib.pyplot as plt

# 定义输入，我们习惯上用一行代表一个数据
X = np.array([[1,3,3],
              [1,4,3],
              [1,1,1],
              [1,2,1]])
# 定义标签，我们习惯上用一行表示一个数据的标签
T = np.array([[1],
              [1],
              [-1],
              [-1]])

# 权值初始化，3行1列
# np.random.random可以生成0-1的随机数
W = np.random.random([3,1])
# 学习率设置
lr = 0.1
# 神经网络输出
Y = 0

# 更新一次权值
def train():
    # 使用全局变量W
    global W
    # 同时计算4个数据的预测值
    # Y的形状为(4,1)-4行1列
    Y = np.sign(np.dot(X,W)) 
    # T - Y得到4个的标签值与预测值的误差E。形状为(4,1)
    E = T - Y 
    # X.T表示X的转置矩阵，形状为(3,4)
    # 我们一共有4个数据，每个数据3个值。定义第i个数据的第j个特征值为xij
    # 如第1个数据，第2个值为x12
    # X.T.dot(T - Y)为一个3行1列的数据：
    # 第1行等于：x00×e0+x10×e1+x20×e2+x30×e3，它会调整第1个神经元对应的权值
    # 第2行等于：x01×e0+x11×e1+x21×e2+x31×e3，它会调整第2个神经元对应的权值
    # 第3行等于：x02×e0+x12×e1+x22×e2+x32×e3，它会影调整3个神经元对应的权值
    # X.shape表示X的形状X.shape[0]得到X的行数，表示有多少个数据
    # X.shape[1]得到列数，表示每个数据有多少个特征值。
    # 这里的公式跟书中公式3.2看起来有些不同，原因是这里的计算是矩阵运算，书中公式3.2是单个元素的计算。如果在草稿子上仔细推算的话你会发现它们的本质是一样的
    delta_W = lr * (X.T.dot(E)) / X.shape[0]
    W = W + delta_W

# 训练100次
for i in range(100):
    #更新一次权值
    train()
    # 打印当前训练次数
    print('epoch:',i + 1)
    # 打印当前权值
    print('weights:',W)
    # 计算当前输出 
    Y = np.sign(np.dot(X,W)) 
    # .all()表示Y中的所有值跟T中所有值都对应相等，结果才为真
    if(Y == T).all(): 
        print('Finished')
        # 跳出循环
        break

#————————以下为画图部分————————#
# 正样本的xy坐标
x1 = [3,4]
y1 = [3,3]
# 负样本的xy坐标
x2 = [1,2]
y2 = [1,1]

# 计算分类边界线的斜率以及截距
# 神经网络的信号总和为w0×x0+w1×x1+w2×x2
# 当信号总和大于0再进过激活函数，模型的预测值会得到1
# 当信号总和小于0再进过激活函数，模型的预测值会得到-1
# 所以当信号总和w0×x0+w1×x1+w2×x2=0时为分类边界线表达式
# 我们在画图的时候把x1，x2分别看成是平面坐标系中的x和y
# 可以得到：w0 + w1×x + w2 × y = 0
# 经过通分：y = -w0/w2 - w1×x/w2，因此可以得到：
k = - W[1] / W[2]
d =  -W[0] / W[2]
# 设定两个点
xdata = (0,5)
# 通过两个点来确定一条直线，用红色的线来画出分界线
plt.plot(xdata,xdata * k + d,'r')
# 用蓝色的点画出正样本
plt.scatter(x1,y1,c='b')
# 用黄色的点来画出负样本
plt.scatter(x2,y2,c='y')
# 显示图案
plt.show()

结果：

  因为权值的初始化使用的是随机的初始化方式，所以每一次训练的周期以及画出来的图 可能都是不一样的。这里我们可以看到单层感知器的一个问题，虽然单层感知器可以顺利地 完成分类任务，但是使用单层感知器来做分类的时候，最后得到的分类边界距离某一个类别 比较近，而距离另一个类别比较远，并不是一个特别理想的分类效果。