@toc

完整代码：https://download.csdn.net/download/qq_43753724/86242828

1、自编码器原理

  先考虑有监督学习中神经网络的功能：

$$o=f_\theta (x),x\in R^{d_{in}}, o\in R^{d_{out}}$$

   $d_{in}$是输入的特征向量长度， $d_{out}$是网络输出的向量长度。对于分类问题，网络模型通过把长度为 $d_{in}$输入特征向量x变换到长度为 $d_{out}$的输出向量o,这个过程可以看成是特征降维的过程，把原始的高维输入向量x变换到低维的变量o。

  特征降维在机器学习中有广泛的应用，如文件压缩、数据预处理等。最常见的降维算法有主成分分析法(Principal Components Analysis,PCA),通过对协方差矩阵进行特征分解而得到数据的主要成分，但是PCA本质上是一种线性变换，提取特征的能力极为有限。

  能否利用神经网络的强大非线性表达能力学习到低维的数据表示？问题的关键在于，训练神经网络一般需要一个显式的标签数据(或监督信号)，但是无监督的数据没有额外的标注信息，只有数据x本身。

  于是，尝试利用数据x本身作为监督信号来知道网络的训练，即希望神经网络能够学习到映射 $f_\theta (x):x\longrightarrow x$。把网络 $f_\theta$切分为两个部分，前面的子网络尝试学习映射关系 $g_{\theta _{1}}:x\longrightarrow z$，后面的自网络尝试学习映射关系 $h_{\theta _{2}}:z\longrightarrow x$。如下图所示。

  把 $g_{\theta _{1}}$看成一个数据编码(Encode)的过程，把高纬度的输入x编码成低纬度的隐变量z，称为Encoder网络(编码器)； $h_{\theta _{2}}$堪称数据解码(Decode)的过程，把编码过后的输入z解码为高纬度的x,称为Decode网络(解码器)。

  编码器和解码器共同完成了输入数据x的编码和解码过程，把整个网络模型 $f_\theta$称为自动编码器(Auto-Encoder),简称自编码器。如果使用深层神经网络来参数化 $g_{\theta _{1}}$和 $h_{\theta _{2}}$函数，则称为深度自编码器，如下图所示。

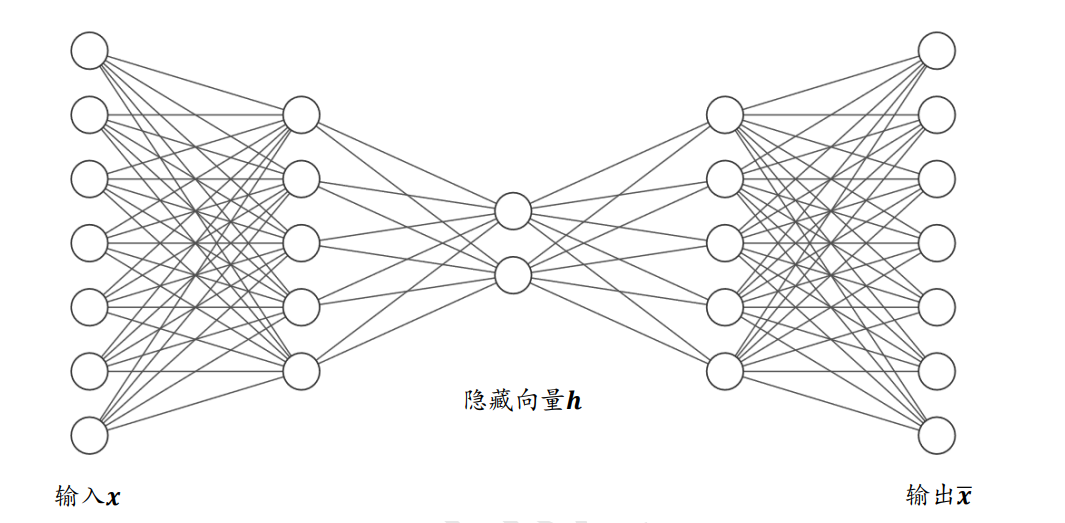
  自编码器能够将输入变换到隐藏向量𝒛，并通过解码器重建(Reconstruct，或恢复)出𝒙 。 我们希望解码器的输出能够完美地或者近似恢复出原来的输入，即𝒙 ≈ 𝒙，那么，自编码器 的优化目标可以写成：

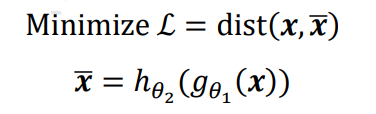
  其中 $dist(x,\bar{x})$表示 𝒙和 $\bar{x}$的距离度量，称为重建误差函数。最常见的度量方法有欧氏距离 (Euclidean distance)的平方，计算方法如下：

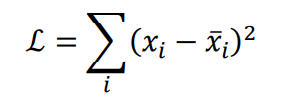
  它和均方误差原理上是等价的。自编码器网络和普通的神经网络并没有本质的区别，只不过训练的监督信号由标签𝒚变成了自身𝒙。借助于深层神经网络的非线性特征提取能力，自编码器可以获得良好的数据表示，相对于 PCA 等线性方法，自编码器性能更加优秀，甚至可以更加完美的恢复出输入𝒙。

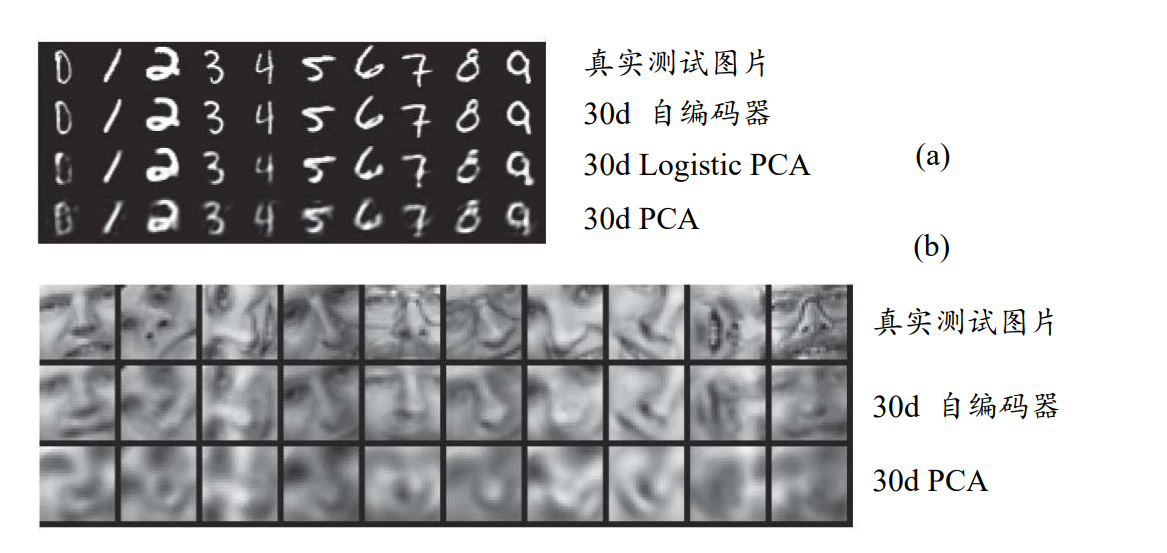
  在下图 (a)中，第 1 行是随机采样自测试集的真实 MNIST 手写数字图片，第 2、3、 4 行分别是基于长度为 30 的隐藏向量，使用自编码器、Logistic PCA 和标准 PCA 算法恢复 出的重建样本图片；在图 (b)中，第 1 行为真实的人像图片，第 2、3 行分别是基于长度为 30 的隐藏向量，使用自编码器和标准 PCA 算法恢复出的重建样本。可以看到，使用 深层神经网络的自编码器重建出图片相对清晰，还原度较高，而 PCA 算法重建出的图片较模糊。

2、FashionMNIST图片重建实战

  自编码器算法非常简单，实现方便，训练也较为稳定，相对于PCA算法，神经网络的强大表达能力可以学习输入的高层抽象的隐藏特征向量z,同时也能够基于z重建出输入。这里基于FashionMNIST数据集进行图片重建实战。

2.1 FashionMNIST数据集

  Fashion MNIST是一个定位在比 MNIST图片识别问题稍复杂的数据集，它的设定与MNIST几乎完全一样，包含了10类不同类型的衣服、鞋子、包等灰度图片，图片大小为28× 28，共70000张图片，其中60000张用于训练集，10000张用于测试集，如图所示，每行是一种类别图片。可以看到，Fashion MNIST除了图片内容与MNIST不一样，其它设定都相同，大部分情况可以直接替换掉原来基于MNIST训练的算法代码，而不需要额外修改。由于Fashion MNIST图片识别相对于MNIST图片更难，因此可以用于测试稍复杂的算法性能。

  在 TensorFlow 中，加载 Fashion MNIST 数据集同样非常方便，利用 keras.datasets.fashion_mnist.load_data()函数即可在线下载、管理和加载。代码如下：

#加载Fashion MNIST图片数据集
(x_train,y_train),(x_test,y_test)=keras.datasets.fashion_mnist.load_data()
#归一化
x_train,x_test=x_train.astype(np.float32)/255.,x_test.astype(np.float32)/255.
#只需要通过图片数据即可构建数据集对象，不需要标签
train_db = tf.data.Dataset.from_tensor_slices(x_train)
train_db = train_db.shuffle(batchsz * 5).batch(batchsz)
test_db = tf.data.Dataset.from_tensor_slices(x_test)
test_db = test_db.batch(batchsz)

print(x_train.shape, y_train.shape)
print(x_test.shape, y_test.shape)

2.2 编码器

  我们利用编码器将输入图片 $x\in R^{784}$降维到较低维度的隐藏向量: $h\in R^{20}$，并基于隐藏向量h利用解码器重建图片，自编码器模型如图所示，编码器由3层全连接层网络组成，输出节点数分别为256、128、20，解码器同样由3层全连接网络组成，输出节点数分别为128、256、784。

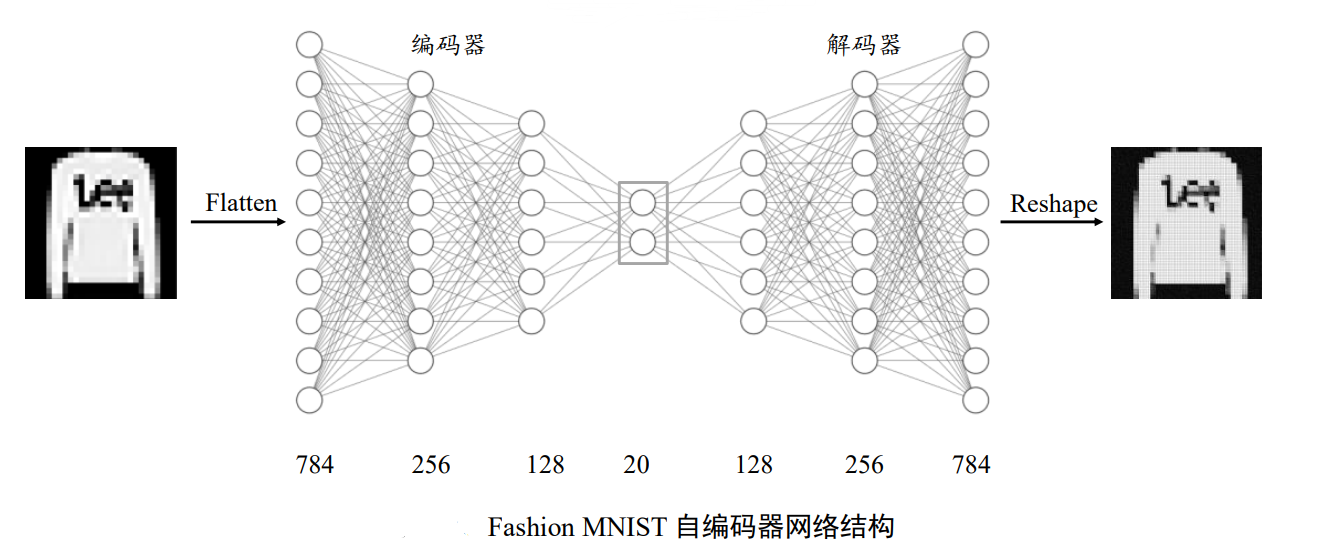
  首先是编码器子网络的实现。利用 3 层的神经网络将长度为 784 的图片向量数据依次 降维到 256、128，最后降维到 h_dim 维度，每层使用 ReLU 激活函数，最后一层不使用激 活函数。代码如下：

		#创建Encoders网络,实现在自编码器类的初始化函数中
        self.encoder=Sequential([
            layers.Dense(256,activation=tf.nn.relu),
            layers.Dense(128,activation=tf.nn.relu),
            layers.Dense(h_dim)
        ])

2.3 解码器

  然后再来创建解码器子网络，这里基于隐藏向量 h_dim 依次升维到 128、256、784 长度，除最后一层，激活函数使用 ReLU 函数。解码器的输出为 784 长度的向量，代表了打 平后的28 × 28大小图片，通过 Reshape 操作即可恢复为图片矩阵。代码如下：

		#创建Decoders网络
        self.decoder=Sequential([
            layers.Dense(128,activation=tf.nn.relu),
            layers.Dense(256,activation=tf.nn.relu),
            layers.Dense(784)
        ])

2.4 自编码器

  上述的编码器和解码器 2 个子网络均实现在自编码器类 AE 中，我们在初始化函数中同时创建这两个子网络。

  接下来将前向传播过程实现在 call 函数中，输入图片首先通过 encoder 子网络得到隐 藏向量 h，再通过 decoder 得到重建图片。依次调用编码器和解码器的前向传播函数即可， 代码如下：

#自编码器类
class AE(keras.Model):
    #自编码器模型类，包含了Encoder和Decoder2个子网络
    def __init__(self):
        super(AE,self).__init__()
        #创建Encoders网络
        self.encoder=Sequential([
            layers.Dense(256,activation=tf.nn.relu),
            layers.Dense(128,activation=tf.nn.relu),
            layers.Dense(h_dim)
        ])
        #创建Decoders网络
        self.decoder=Sequential([
            layers.Dense(128,activation=tf.nn.relu),
            layers.Dense(256,activation=tf.nn.relu),
            layers.Dense(784)
        ])
    
    def call(self,inputs,training=None):
        #前向传播函数
        #编码获得隐藏向量h,[b,784]=>[b,20]
        h=self.encoder(inputs)
        #解码获得重建图片,[b,20]=>[b,784]
        x_hat=self.decoder(h)
        
        return x_hat

2.5 网络训练

  自编码器的训练过程与分类器的基本一致，通过误差函数计算出重建向量 $\bar{x}$与原始输 入向量𝒙之间的距离，再利用 TensorFlow 的自动求导机制同时求出 encoder 和 decoder 的梯度，循环更新即可。

  首先创建自编码器实例和优化器，并设置合适的学习率。

#创建自编码器实例和优化器，并设置合适的学习率
#创建网路对象
model=AE()
#指定输入大小
model.build(input_shape=(4,784))
#打印网络信息
model.summary()
#创建优化器，并设置学习率
optimizer=keras.optimizers.Adam(lr=lr)

  这里固定训练 100 个 Epoch，每次通过前向计算获得重建图片向量，并利用 tf.nn.sigmoid_cross_entropy_with_logits 损失函数计算重建图片与原始图片直接的误差，实际上利用 MSE 误差函数也是可行的。代码如下：

for epoch in range(100):#训练100个Epoch
    for step,x in enumerate(train_db):#遍历训练集
        #打平，[b,28,28]=>[b,784]
        x=tf.reshape(x,[-1,784])
        #构建梯度记录器
        with tf.GradientTape() as tape:
            #前向计算获得重建的图片
            x_rec_logits=model(x)
            #计算重建图片与输入之间的损失函数
            rec_loss=tf.nn.sigmoid_cross_entropy_with_logits(labels=x,logits=x_rec_logits)
            #计算均值
            rec_loss=tf.reduce_mean(rec_loss)
        #自动求导，包含了2个子网络的梯度
        grads=tape.gradient(rec_loss,model.trainable_variables)
        #自动更新，同时更新2个子网络
        optimizer.apply_gradients(zip(grads,model.trainable_variables))
        
        if step%100==0:
            #间隔性打印训练误差
            print(epoch,step,float(rec_loss))

2.6 图片重建

  与分类问题不同的是，自编码器的模型性能一般不好量化评价，尽管ℒ值可以在一定程度上代表网络的学习效果，但我们最终希望获得还原度较高、样式较丰富的重建样本。 因此一般需要根据具体问题来讨论自编码器的学习效果，比如对于图片重建，一般依赖于人工主观评价图片生成的质量，或利用某些图片逼真度计算方法(如 Inception Score 和 Frechet Inception Distance)来辅助评估。

  为了测试图片重建效果，我们把数据集切分为训练集与测试集，其中测试集不参与训 练。我们从测试集中随机采样测试图片 $x\in D^{test}$，经过自编码器计算得到重建后的图片， 然后将真实图片与重建图片保存为图片阵列，并可视化，方便比对。代码如下：

#测试
        #重建图片，从测试集采样一批图片
        x=next(iter(test_db))
        #打平送入自编码器
        logits=model(tf.reshape(x,[-1,784]))
        #将输出转换为像素值，使用sigmoid函数
        x_hat=tf.sigmoid(logits)
        
        #恢复为28*28,[b,784]=>[b,28,28]
        x_hat=tf.reshape(x_hat,[-1,28,28])
        
        #输入的前50张+重建的前50张图片合并(在第1个维度拼接)，[b,28,28]=>[2b,28,28]
        x_concat=tf.concat([x[:50],x_hat[:50]],axis=0)
        #恢复为0-255
        x_concat=x_concat.numpy()*255.
        #转化为整型
        x_concat=x_concat.astype(np.uint8)
        #保存图片
        save_images(x_concat,'ae_images/rec_epoch_%d.png'%epoch)

  图片重建的效果如图 所示，其中每张图片的左边5列为真实图片，右边5列为对应的重建图片。可以看到，第一个 Epoch时，图片重建效果较差，图片非常模糊，逼真度较差;随着训练的进行，重建图片边缘越来越清晰，第100个Epoch时，重建的图片效果已经比较接近真实图片。

  这里的 save_images 函数负责将多张图片合并并保存为一张大图，这部分代码使用 PIL 图片库完成图片阵列逻辑，代码如下：

#save_images函数负责将多张图片合并并保存为一张大图，使用PIL图片库完成图片阵列逻辑
def save_images(imgs,name):
    #创建280*280大小图片阵列
    new_im=Image.new('L',(280,280))
    index=0
    for i in range(0,280,28):#10行图片阵列
        for j in range(0,280,28):#10列图片阵列
            im=imgs[index]
            im=Image.fromarray(im,mode='L')
            new_im.paste(im,(i,j))#写入对应位置
            index+=1
    #保存图片阵列
    new_im.save(name)

  迭代100次：

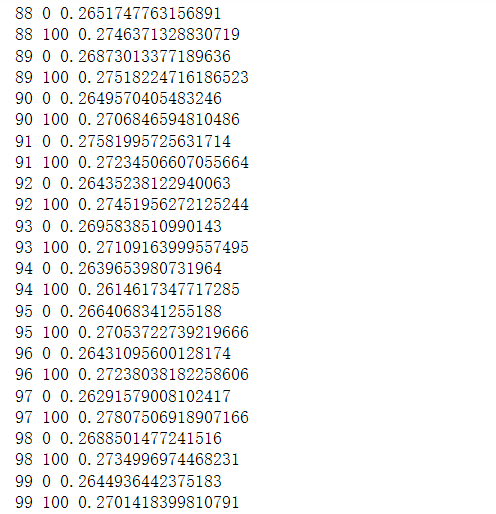
  重建的100张图片：