详解二叉树遍历(C/C++)
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档
文章目录
一、先序遍历
1.知识点概述
若二叉树为空,则空操作返回,否先访问根结点,然后先序遍历左子树,再先序遍历右子树
简记 : 根左右
2.图片理解
顺序为 A B D E C F G
思路:
3.代码
代码如下
二、中序遍历
1.知识点概述
中序遍历是指中序遍历根结点的左子树,然后访问根结点,在中序遍历右子树(左子树为空或者已经遍历才能访问根)
简记:左根右
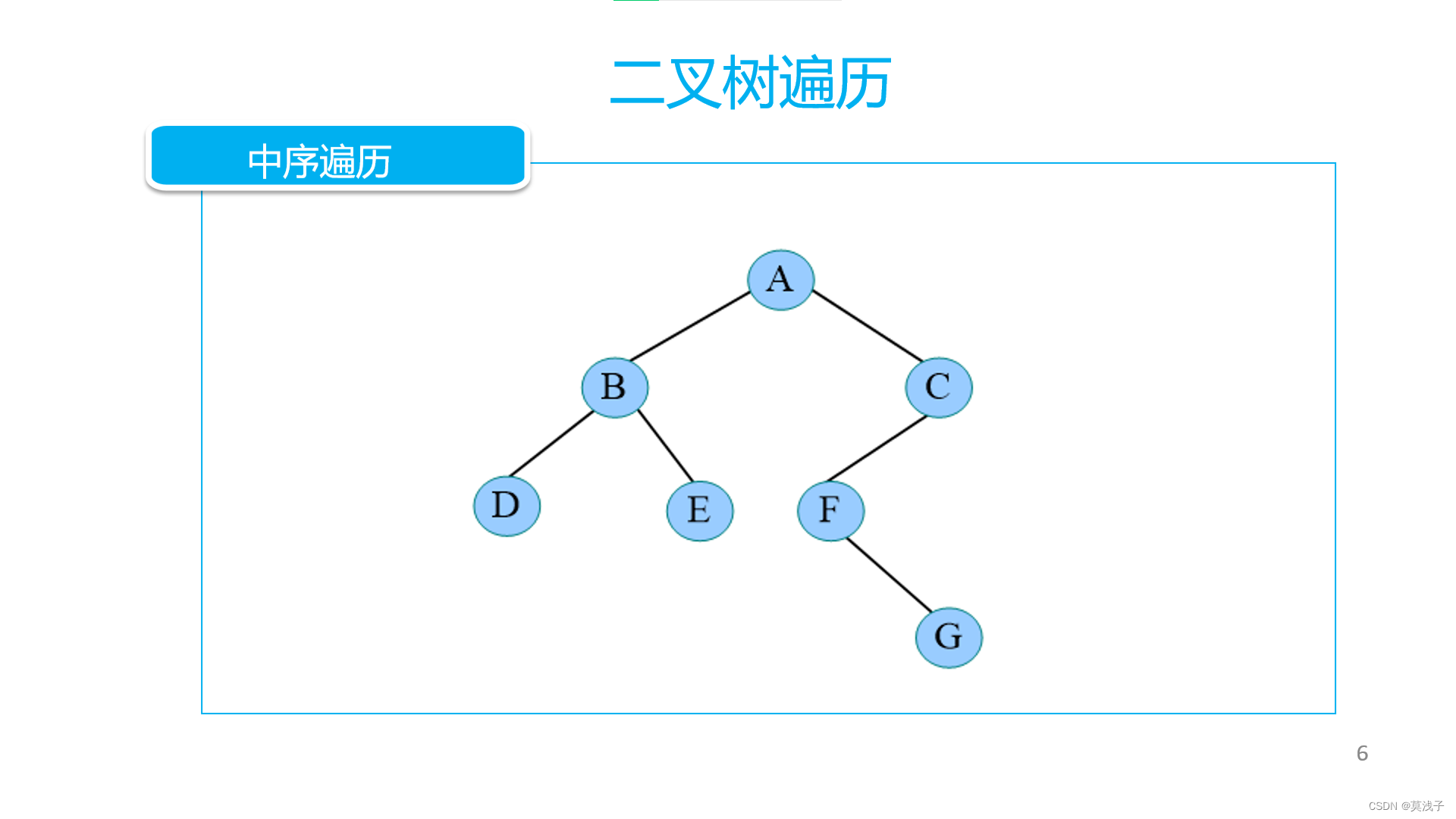
2.图片理解
顺序为 D B E A F G C
最开始看A的左节点B, B的最结点不为空,然后看D,D的左节点为空,访问D,然后此时的
B做左节点D,已经遍历,可以访问B,然后看E,E因为左节点为空,可以访问,然后看根结点A,访问A,看 C ,C结点不为空看F,F左节点为空,可以访问F,G的左节点为空,访问G,最后C的左节点完成访问,可以访问C。
3.代码
代码如下
三、后序遍历
1.知识点概念
后序遍历是指后序遍历左子树,后序遍历右子树,然后访问根(左子树、右子树为空或已遍历才能访问根)
简记:左右根
2.图片理解
最开始看B,但是B不满足条件左右都不为空,所以不遍历,所以遍历D,因D左右子树皆为空,访问D,然后看E,它的左右子树为空,所以访访问E,B的左右结点都已经遍历可以访问B,然后看C,C的左节点不为空,看F,F的右节点不为空,看G,G满足条件,访问G,此时F左为空,右已遍历,可以访问F,然后F遍历了,C右又为空,所以C可以访问,最后访问A。
最终顺序为:D E B G F C A
3.代码
代码如下
四、层序遍历
1.知识点概述
从根结点开始访问,从上到下逐层遍历,在同一层中,按照从左到右的顺序逐个访问
2.图片理解
顺序为 A B C D E F G
算法思想:
① 初始化一个辅助队列
②根结点入队
③若队列非空,则对头结点出队,访问该节点,并将其左右孩子插入队尾
3.代码
代码如下
五、二叉树的建立
1.补空法
补空法是指如果左子树或右子树为空时,用特殊字符补空,如 “#”,然后按照先序遍历的顺序,得到先序遍历序列,根据该序列创建二叉树
步骤
输入补空后的二叉树先序遍历序列;
如果ch = '#',T = NULL; 否则创建一个新结点T,令 T->date = ch; 递归创建T的左子树,递归创建T的右子树。
代码如下:
六、二叉树的还原
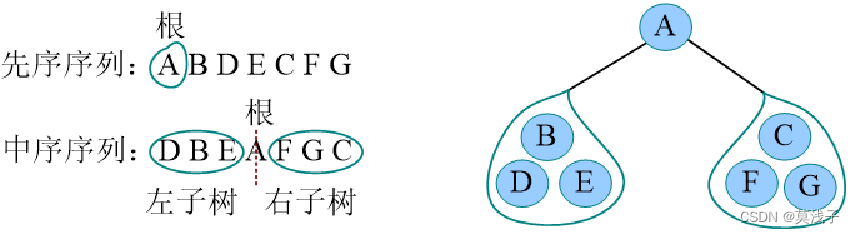
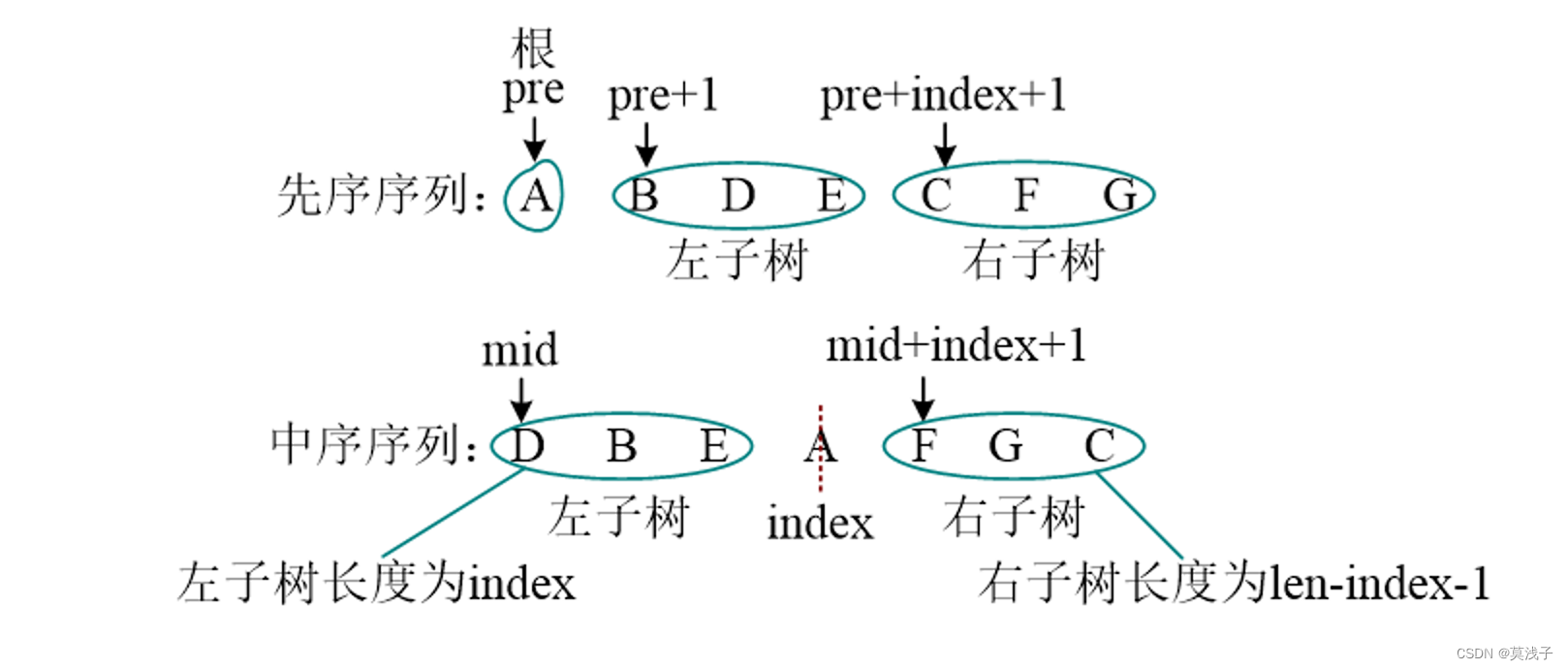
列如 :已知一棵二叉树的先序序列ABDECFG 和中序序列DBEAFGC,画出这棵二叉树。
1.算法步骤
1. 先序序列的第一个字符为根;
2. 在中序列中,以根为中心划分左右子树;
3. 还原左右子树。
2.代码
总结(二叉树的四种遍历代码)
- 点赞
- 收藏
- 关注作者





评论(0)