​

 提示：记得点赞关注加收藏

提示：以下是本篇文章参考《算法训练营》

一、概念

邻接表是图的一种链式存储方法，其数据结构包括两部分：节点和邻接点。

二、分类 

1）无向图的邻接表

例如，一个无向图及其邻接表如下图所示。一个节点的所有邻接点构成一个单链表

​编辑

解释：

• 节点a 的邻接点是节点b 、d ，其邻接点的存储下标为1、3，按照头插法（逆序）将其放入节点a 后面的单链表中；

• 节点b 的邻接点是节点a 、c 、d ，其邻接点的存储下标为0、2、3，将其放入节点b 后面的单链表中；

• 节点c 的邻接点是节点b、d ，其邻接点的存储下标为1、3，将其放入节点c 后面的单链表中；

• 节点d 的邻接点是节点a、b、c ，其邻接点的存储下标为0、1、2，将其放入节点d 后面的单链表中。

无向图邻接表的特点如下。

• 如果无向图有n 个节点、e 条边，则节点表有n 个节点，邻接点表有2e 个节点。

• 节点的度为该节点后面单链表中的节点数。

在上图中，节点数n =4，边数e =5，则在该图的邻接表中，节点表有4个节点，邻接点表有10个节点。节点a 的度为2，其后面单链表中的节点数为2；节点b 的度为3，其后面单链表中的节点数为3。

2）有向图的邻接表（出弧）

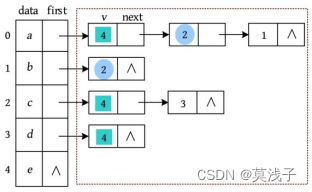
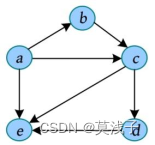
例如，一个有向图及其邻接表如下图所示。

​编辑

解释：

• 节点a 的邻接点（只看出边，即出弧）是节点b、c、e ，其邻接点的存储下标为1、2、4，按照头插法（逆序）将其放入节点a 后面的单链表中；

• 节点b 的邻接点是节点c ，其邻接点的存储下标为2，将其放入节点b 后面的单链表中；

• 节点c 的邻接点是节点d、e ，其邻接点的存储下标为3、4，按头插法将其放入节点c 后面的单链表中；

• 节点d 的邻接点是节点e ，其邻接点的存储下标为4，将其放入节点d 后面的单链表中；

• 节点e 没有邻接点，其后面的单链表为空。

注意： 对有向图中节点的邻接点，只看该节点的出边（出弧）。
 

有向图的邻接表的特点如下。

• 如果有向图有n 个节点、e 条边，则节点表有n 个节点，邻接点表有e 个节点。

• 节点的出度为该节点后面单链表中的节点数。

在上图中，节点数n =5，边数e =7，则在该图的邻接表中，节点表有5个节点，邻接点表有7个节点。节点a 的出度为3，其后面单链表中的节点数为3；节点c 的出度为2，其后面单链表中的节点数为2。

在有向图邻接表中很容易找到节点的出度，但是找入度很难，需要遍历所有邻接点表中的节点，查找到该节点出现了多少次，入度就是多少。例如在下图中，节点c 的下标为2，在邻接点表中有两个为2的节点，因此节点c 的入度为2；节点e 的下标为4，在邻接点表中有3个为4的节点，因此节点e 的入度为3。

​编辑

3）有向图的逆邻接表（入弧）

有时为了方便得到节点的入度，可以建立一个有向图的逆邻接表，如下图所示。

​编辑

解释：

• 节点a 没有逆邻接点（只看入边，即入弧），其后面的单链表为空；

• 节点b 的逆邻接点是节点a ，其邻接点的存储下标为0，将其放入节点b 后面的单链表中；

• 节点c 的逆邻接点是a、b ，其邻接点的存储下标为0、1，按照头插法将其放入节点c 后面的单链表中；

• 节点d 的逆邻接点是节点c ，其邻接点的存储下标为2，将其放入节点d 后面的单链表中；

• 节点e 的逆邻接点是节点a、c、d ，其邻接点的存储下标为0、2、3，按照头插法（逆序）将其放入节点e 后面的单链表中。

注意： 对有向图中节点的逆邻接点，只看该节点的入边（入弧）。

有向图的逆邻接表的特点如下。

（1）如果有向图有n 个节点、e 条边，则节点表有n 个节点，邻接点表有e 个节点。

（2）节点的入度为该节点后面的单链表中的节点数。

在上图中，节点数n =5，边数e =7，在该图的邻接表中，节点表有5个节点，邻接点表有7个节点。节点a 的入度为其后面的单链表中的节点数0，节点c 的入度为其后面的单链表中的节点数2。

 三.步骤

算法步骤： 

（1）输入节点数和边数；

（2）依次输入节点信息，将其存储到节点数组Vex[]的data域中，将Vex[]的first域置空；

（3）依次输入每条边依附的两个节点，如果是网，则还需要输入该边的权值。

• 如果是无向图，则输入a b ，查询节点a、b 在节点数组Vex[]中的存储下标i 、j ，创建一个新的邻接点s ，令s ->v =j ; s ->next=NULL；然后将节点s 插入第i 个节点的第1个邻接点之前（头插法）。在无向图中，从节点a 到节点b 有边，从节点b 到节点a 也有边，因此还需要创建一个新的邻接点s 2 ，令s 2 ->v =i ; s 2 ->next=NULL；然后将s 2 节点插入第j 个节点的第1个邻接点之前（头插法）。

• 如果是有向图，则输入a b ，查询节点a、b 在节点数组Vex[]中的存储下标i 、j ，创建一个新的邻接点s ，令s ->v =j ; s ->next=NULL；将节点s 插入第i 个节点的第1个邻接点之前（头插法）。

• 如果是无向网或有向网，则和无向图或有向图的处理方式一样，只是邻接点多了一个权值域。

图解： 一个有向图如下图所示，其邻接表的存储过程如下所述。

                                          ​编辑

（1）输入节点数5和边数7，G .vexnum=5，G .edgenum=7。

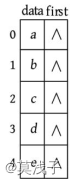
（2）输入节点信息a b c d e 并将其存入节点表，存储结果如下图所示。

    ​编辑

（3）依次输入每条边依附的两个节点。

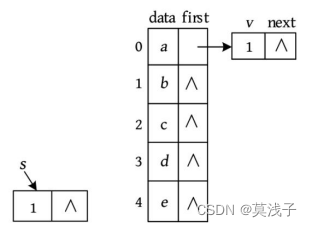
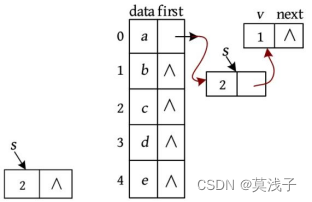
• 输入a b ，处理结果：在Vex[]数组的data域中查找到节点a 、b 的下标分别为0、1，创建一个新的邻接点s ，令s ->v =1; s ->next=NULL。将节点s 插入第0个节点的第1个邻接点之前（头插法）。

​编辑

• 输入a c ，处理结果：在Vex[]数组的data域中查找到节点a 、c 的下标分别为0、2，创建一个新的邻接点s ，令s ->v=2; s ->next=NULL。将节点s 插入第0个节点的第1个邻接点之前（头插法）。

​编辑

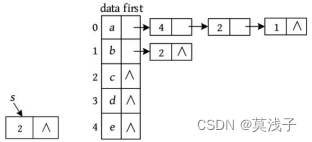
• 输入a e ，处理结果：在Vex[]数组的data域中查找到节点a 、e 的下标分别为0、4，创建一个新的邻接点s ，令s ->v =4; s ->next=NULL。将节点s 插入第0个节点的第1个邻接点之前（头插法）。

​编辑

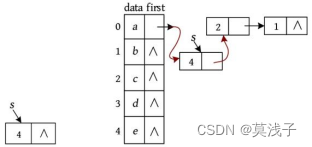
 • 输入b c ，处理结果：在Vex[]数组的data域中查找到节点b 、c 的下标分别为1、2，创建一个新的邻接点s ，令s ->v =2; s ->next=NULL。将节点s 插入第1个节点的第1个邻接点之前（头插法）。

​编辑

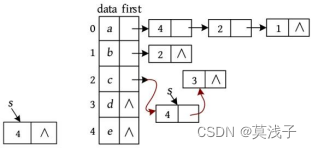
• 输入c d ，处理结果：在Vex[]数组的data域中查找到节点c 、d 的下标分别为2、3，创建一个新的邻接点s ，令s ->v =3; s ->next=NULL。将节点s 插入第2个节点的第1个邻接点之前（头插法）。

​编辑

• 输入c e ，处理结果：在Vex[]数组的data域中查找到c 、e 的下标分别为2、4，创建一个新的邻接点s ，令s ->v =4; s ->next=NULL。将节点s 插入第2个节点的第1个邻接点之前（头插法）。

​编辑

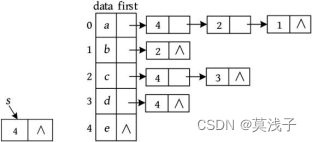
• 输入d e ，处理结果：在Vex[]数组的data域中查找到节点d 、e 的下标分别为3、4，创建一个新的邻接点s ，令s ->v =4; s ->next=NULL。将节点s 插入第3个节点的第1个邻接点之前（头插法）。

​编辑

注意： 由于后输入的内容被插在了单链表的前面，因此若输入顺序不同，则建立的单链表也不同。

四、代码

代码如下

//创建有向图的邻接表
#include <iostream>
using namespace std;
const int MaxVnum=100;//顶点数最大值

typedef char VexType;//顶点的数据类型为字符型
typedef struct AdjNode{ //定义邻接点类型
	int v; //邻接点下标
	struct AdjNode *next; //指向下一个邻接点
}AdjNode;

typedef struct VexNode{ //定义顶点类型
	VexType data; // VexType为顶点的数据类型，根据需要定义
	AdjNode *first; //指向第一个邻接点
}VexNode;

typedef struct{//定义邻接表类型
    VexNode  Vex[MaxVnum];
    int vexnum,edgenum; //顶点数，边数
}ALGragh;

int locatevex(ALGragh G,VexType x)
{
    for(int i=0;i<G.vexnum;i++)//查找顶点信息的下标
       if(x==G.Vex[i].data)
        return i;
    return -1;//没找到
}

void insertedge(ALGragh &G,int i,int j)//插入一条边
{
    AdjNode *s;
    s=new AdjNode;
    s->v=j;
    s->next=G.Vex[i].first;
    G.Vex[i].first=s;
}

void printg(ALGragh G)//输出邻接表
{
   cout<<"----------邻接表如下：----------"<<endl;
   for(int i=0;i<G.vexnum;i++)
   {
       AdjNode *t=G.Vex[i].first;
       cout<<cout<<G.Vex[i].data<<"：  ";
       while(t!=NULL)
       {
           cout<<"["<<t->v<<"]  ";
           t=t->next;
       }
       cout<<endl;
   }
}

void CreateALGraph(ALGragh &G)//创建有向图邻接表
{
    int i,j;
    VexType u,v;
    cout<<"请输入顶点数和边数:"<<endl;
    cin>>G.vexnum>>G.edgenum;
    cout << "请输入顶点信息:"<<endl;
    for(i=0;i<G.vexnum;i++)//输入顶点信息，存入顶点信息数组
        cin>>G.Vex[i].data;
    for(i=0;i<G.vexnum;i++)
        G.Vex[i].first=NULL;
    cout<<"请依次输入每条边的两个顶点u,v"<<endl;
    while(G.edgenum--)
    {
        cin>>u>>v;
        i=locatevex(G,u);//查找顶点u的存储下标
        j=locatevex(G,v);//查找顶点v的存储下标
        if(i!=-1&&j!=-1)
            insertedge(G,i,j);
        else
        {
           cout << "输入顶点信息错！请重新输入！"<<endl;
           G.edgenum++;//本次输入不算
        }
    }
}

int main()
{
    ALGragh G;
    CreateALGraph(G);//创建有向图邻接表
    printg(G);//输出邻接表
    return 0;
}

​