​

 目录

一、生成树

二、最小生成树（代价最小树）

三、求最小生成树

1、Prim算法（普里姆） 

2.Kruskal 算法（克鲁斯卡尔）

3.Prim算法和Kruskal算法对比

一、生成树

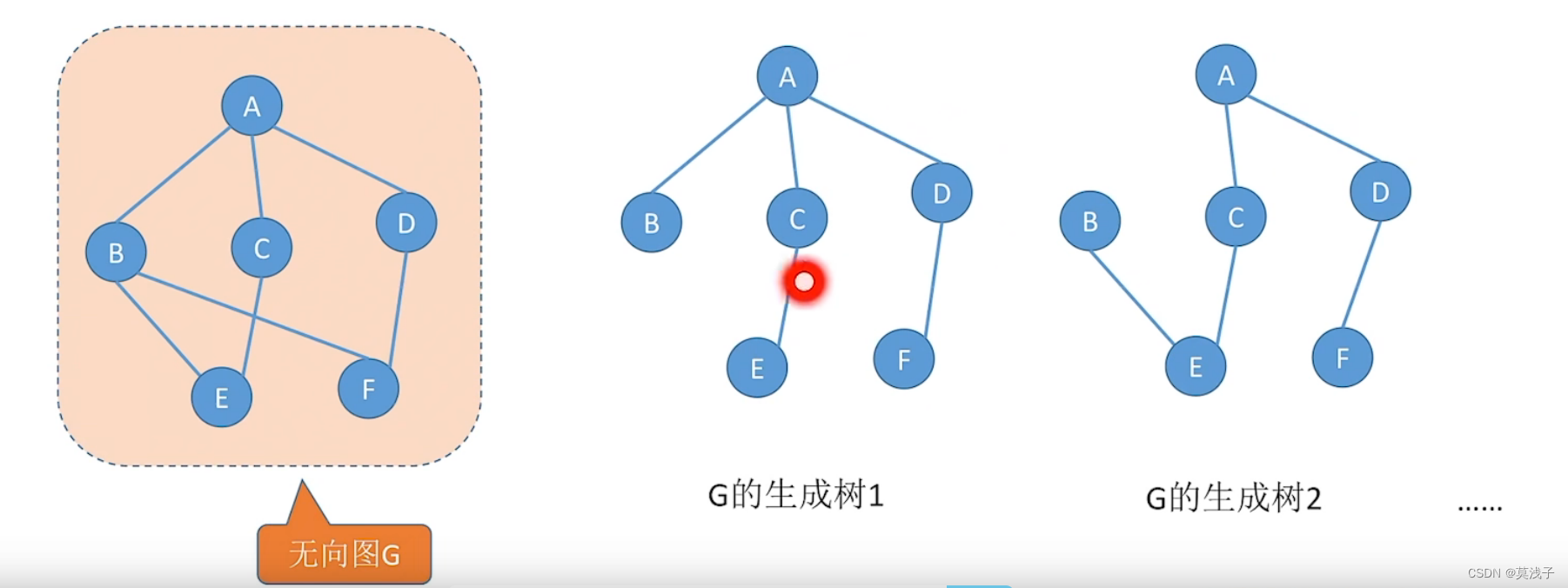
连通图的生成树是包含图中全部顶点的一个极小连通子图。

边尽可能少，但要保持连通

若图中顶点数为n，则它的生成树含有n-1条边。对生成树而言，若砍去它的一条边，则会变成非连通图，若加上一条边则会形成一个回路。

一个连通图可能有多个连通树
 

​编辑

二、最小生成树（代价最小树）

对于一个带权连通无向图G=(V, E)，生成树不同，每棵树的权（即树中所有边上的权值之和)也可能不同。设R为G的所有生成树的集合，若T为R中边的权值之和最小的生成树，则T称为G的最小生成树（Minimum-Spanning-Tree,MST) 。

最小生成树可能有多个，但边的权值之和总是唯一且最小的

最小生成树的边数=顶点数–1。砍掉一条则不连通，增加一条边则会出现回路

如果一个连通图本身就是—棵树，则其最小生成树就是它本身

只有连通图才有生成树，非连通图只有生成森林

三、求最小生成树

1、Prim算法（普里姆） 

Prim算法（普里姆):
从某一个顶点开始构建生成树;每次将代价最小的新顶点纳入生成树，直到所有顶点都纳入为止。

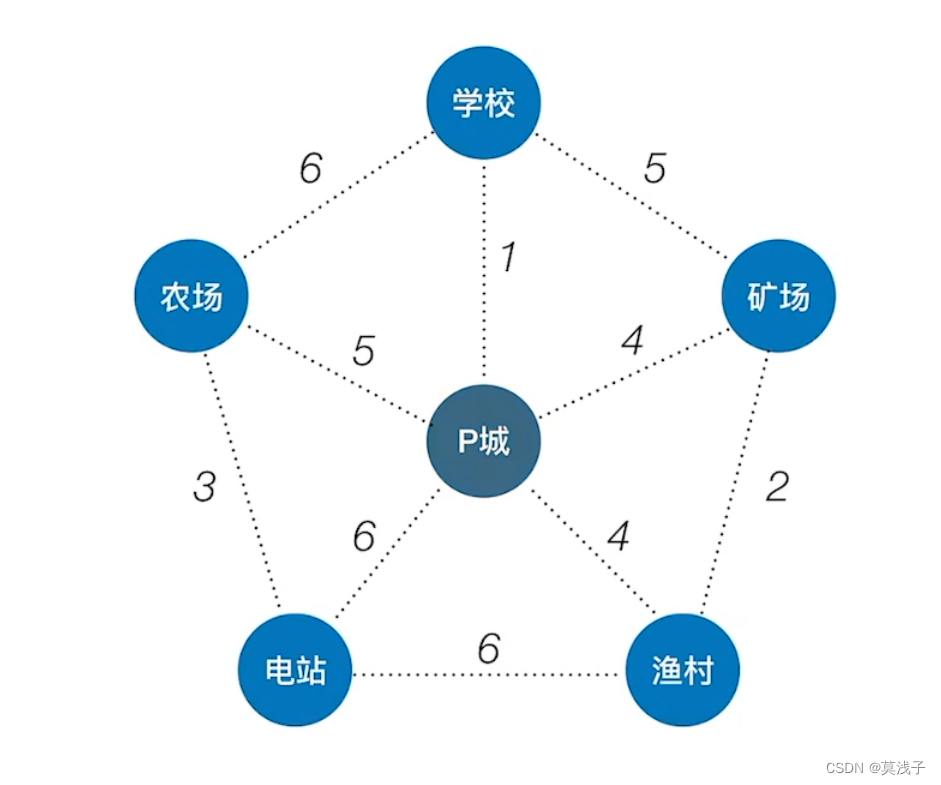
具体该如何实现呢，以下面的为例

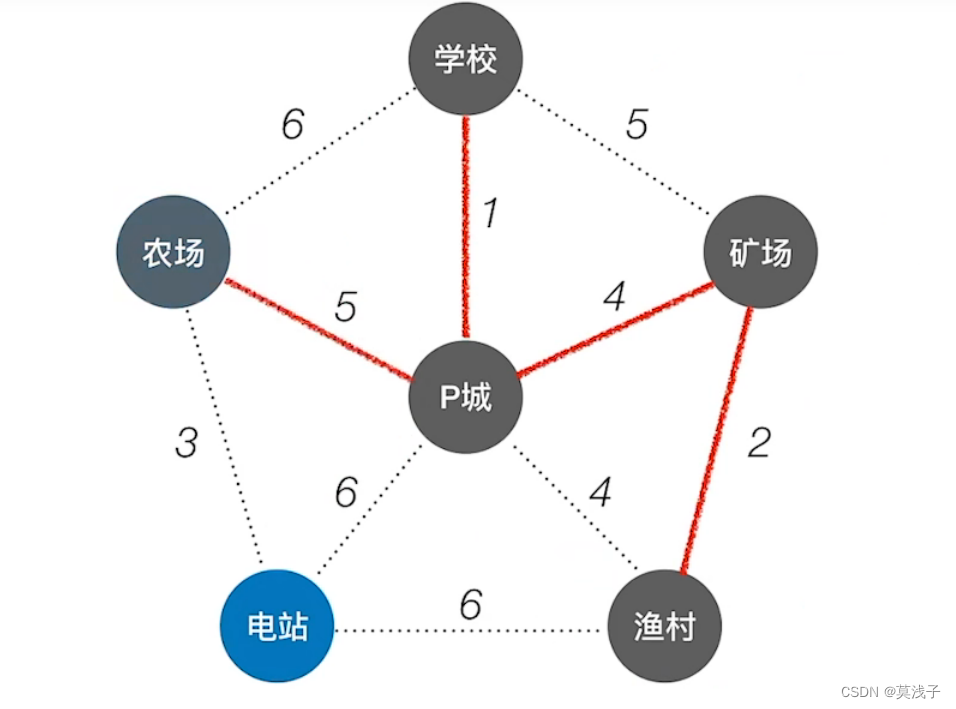
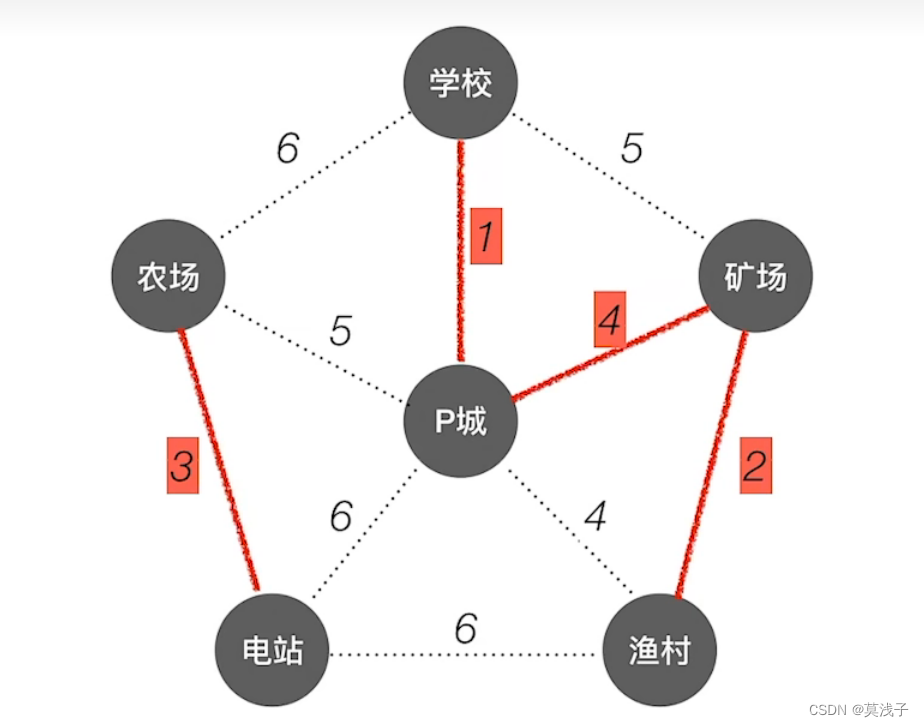
从P城出发找最小生成树,从P城出发。

​

编辑

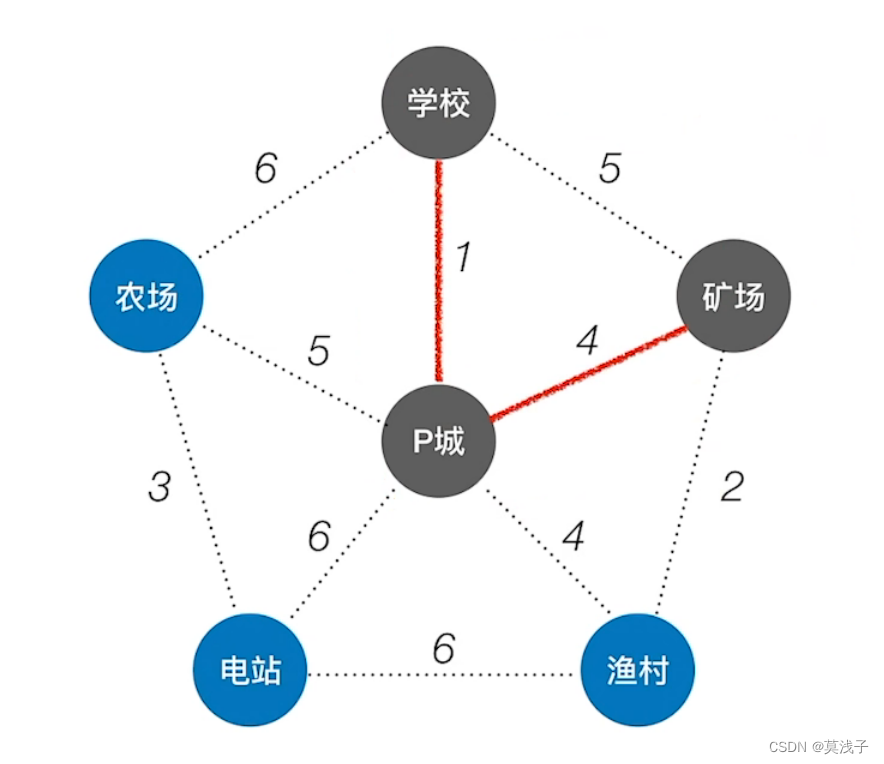
 P到学校的代价最小是1，最小所以P城连接学校

​

编辑

 然后找那个点，到P城和学校形成的树中，最小代价的，我们可以看到，只有矿场到P城是最小的

所以连接P城和矿场。（如果选下面的4最终图不一样，但是最终最小代价一样）

​

编辑

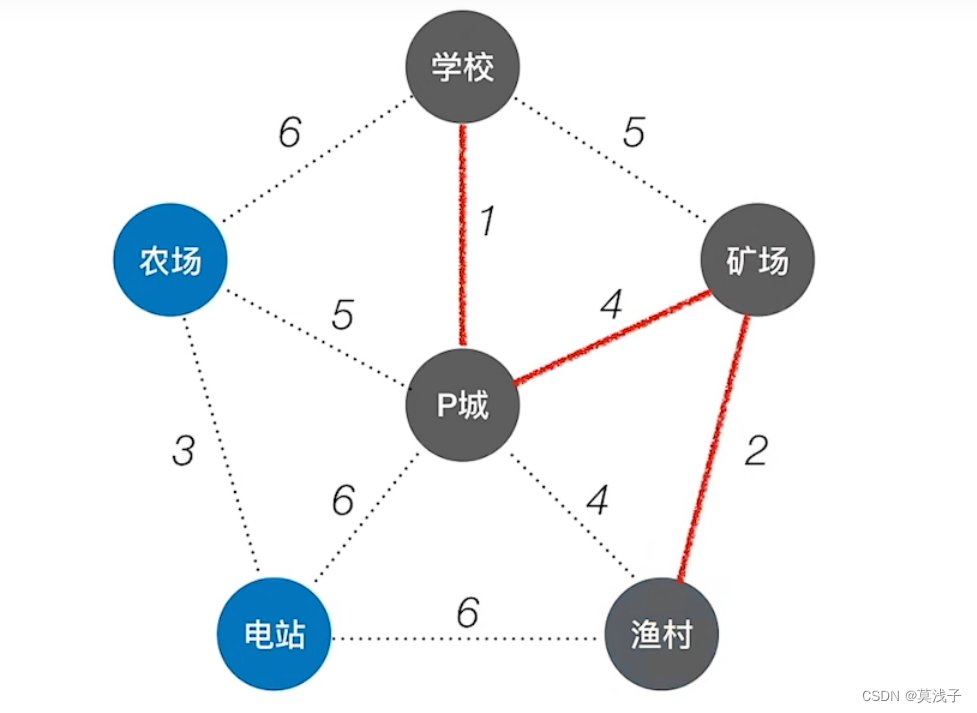
然后看哪个点到这个三个点形成的树最小的代价，知道渔村是最小的，连接矿场和渔村。

​

编辑

在寻找是剩下俩个结点中到这棵树的最下代价，易知是农场到P城的路径最小。

​

编辑

 最后还剩一个电站与农场相连路径最短为3 。

​

编辑

 这个也是最终的最小生成树（红线连接部分）

2.Kruskal 算法（克鲁斯卡尔）

Kruskal算法(克鲁斯卡尔)∶
每次选择一条权值最小的边，使这条边的两头连通(原本已经连通的就不选)
直到所有结点都连通

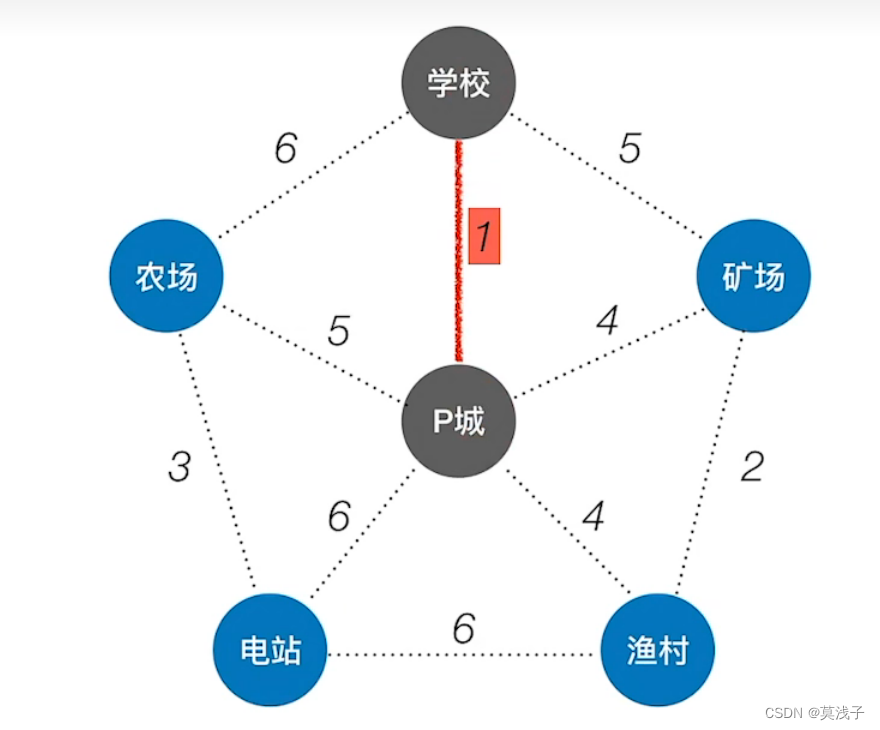
 任然是这个图

​

编辑

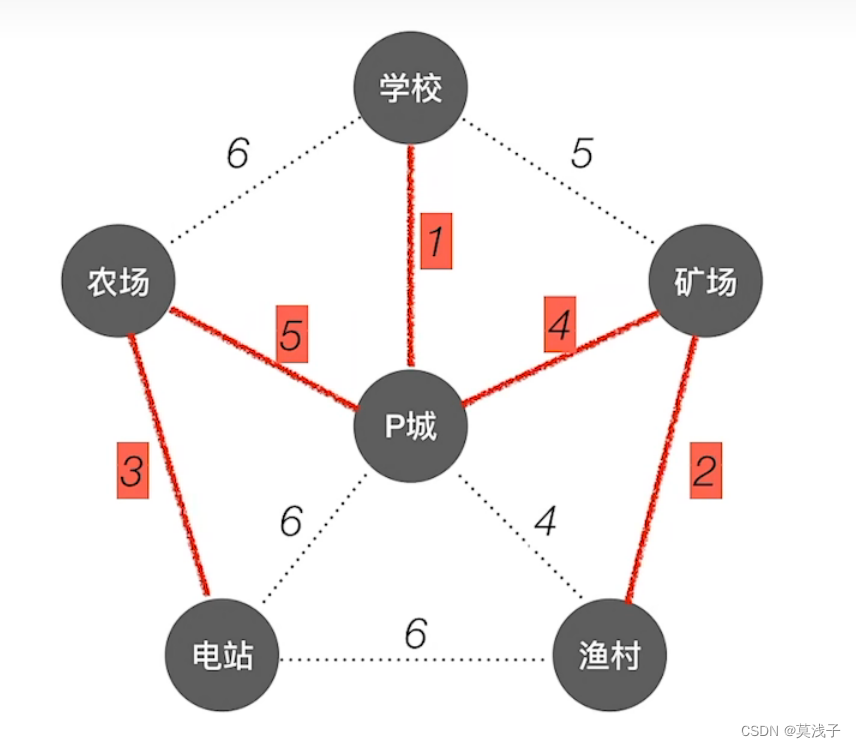
按照克鲁斯卡尔算法，找到一个最小的权值的边，是学校和P城

​

编辑

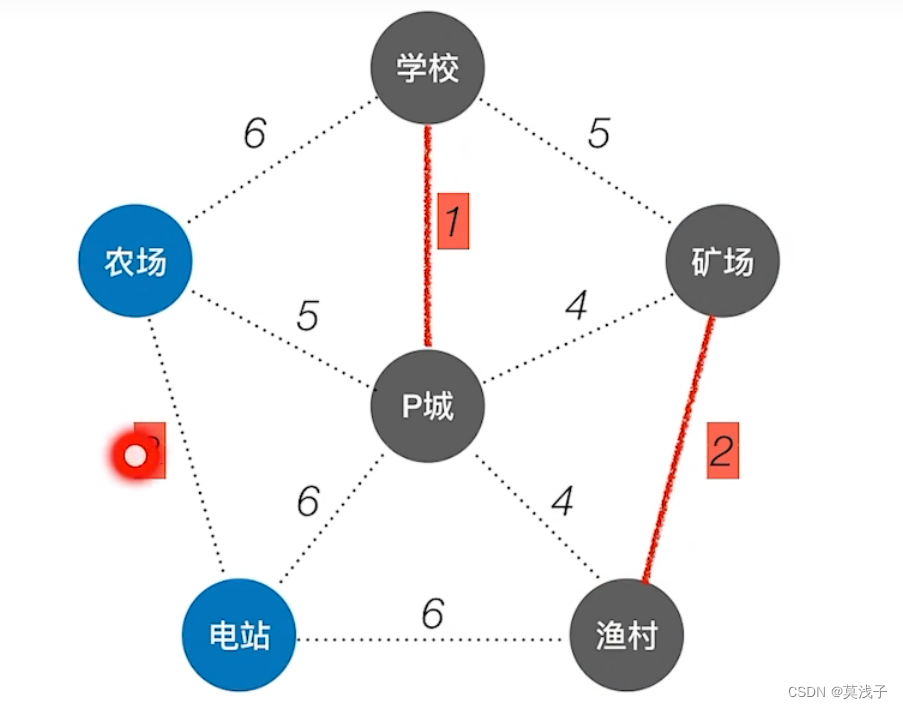
 然后在找到是矿场和渔村，且俩个点不连通，可以选。

​

编辑

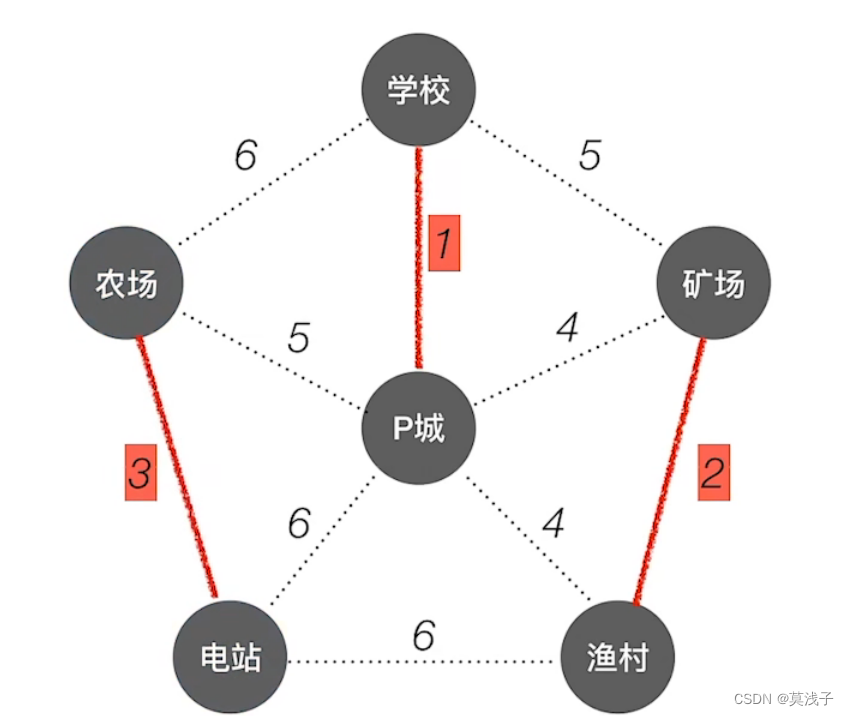
然后找权值最小的边是渔村和电站为3，且俩个点目前不连通·

​

编辑

在从剩余的边中找到权值最小的，有俩个是P城和矿场以及P城和渔村，随便选都行。虽然最终图不一样，但是最小代价一样。

​

编辑

然后找最小，发现是P城和渔村，但是P城和渔村是连通的。所以不选，在找，权值是5的有俩个，然而，学校和矿场确是俩通的，只能选农场和P城，选完以后发现全部连通

​

编辑

3.Prim算法和Kruskal算法对比

​编辑

​