详解数据结构——二叉排序树
目录
二叉排序树
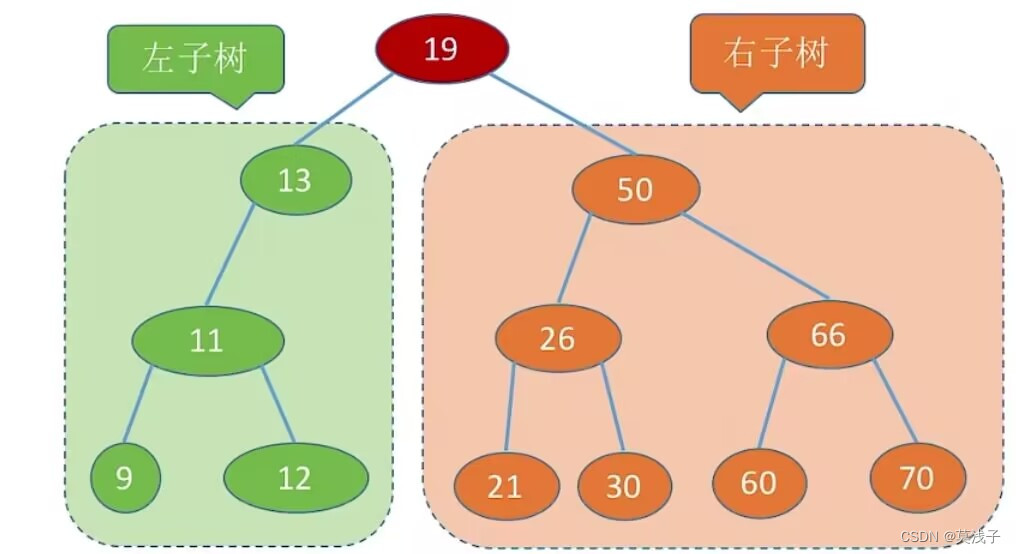
二叉排序树，又称二叉查找树（BST，Binary Search Tree)一棵二叉树或者是空二叉树，或者是具有如下性质的二叉树:
左子树上所有结点的关键字均小于根结点的关键字;
右子树上所有结点的关键字均大于根结点的关键字。左子树和右子树又各是一棵二叉排序树
左子树结点值<根结点值<右子树结点值
进行中序遍历可以得到一个递增的有序序列
二叉排序树的查找
若树非空，目标值与根结点的值比较:
若相等，则查找成功;
若小于根结点，则在左子树上查找，否则在右子树上查找。若查找成功，返回结点指针：查找失败返回NULL
代码
//二叉排序树结点
typedef struct BSTNode{
int key;
struct BSTNode *lchild ,*rchild;
}BSTNode,*BSTtree;
//在二叉排序树中找到值为key的结点 ,时间复杂度最后 O(1)
BSTNode *BST_Search(BSTree T,int key){
while(T!=NULL &&key != T->key ){ //若树空或等于根结点，循环结束
if(key < T->key) T = T -> lchild; //小于，左子树查找
else T = T -> rchild; //大于，右子树查找
}
return T;
}
//在二叉排序树中找到值为key的结点--递归实现 ,时间复杂度最坏O(h) h 是树的高度
BSTNode *BST_Search(BSTree T,int key){
if(T = NULL)
return NULL; //查找失败
if(key == T->key)
return T; //查找成功
else if (key < T->lchild)
return BSTSearch(T->lchild,key); //在左子树中查找
else
return BSTSearch(T->rchild,key);
}二叉排序树的插入
若原二叉排序树为空，则直接插入结点;否则，
若关键字k小于根结点值，则插入到左子树，
若关键字k大于根结点值，则插入到右子树
代码
最坏时间复杂度O(h) ，树的高度
//在二叉排序树插入关键字为k的新结点（递归实现)
int BST_Insert(BSTree &T, int k){
if(T==NULL){ //原树为空，新插入的结点为根结点
T=(BSTree)malloc(sizeof(BSTNode) );
T->key = k;
T->lchild = T->rchild = NULL;
return 1; //返回1，插入成功
}
else if(k==T->key) //树中存在相同关键字的结点，插入失败
return 0;
else if(k<T->key) //插入到T的左子树
return BST_Insert(T-lchild,k);
else //插入到T的右子树
return BST_Insert(T->rchild,k);
}
二叉排序树的构造
//按照str[]中的关键字序列建立二叉排序树
void Creat_BST(BSTree &T,int str[],int n){
T = NULL; //初始时T为空树
int i = 0;
while (i < n){ //依次将每个关键字插入到二叉排序树中
BST_Insert(T,str[i]);
i++;
}
}
二叉排序树的删除
先搜索找到目标结点:
1、若被删除结点z是叶结点，则直接删除，不会破坏二叉排序树的性质。
2、若结点z只有一棵左子树或右子树，则让z的子树成为z父结点的子树，替代z的位置。
3、若结点z有左、右两棵子树，则令z的直接后继（或直接前驱）替代z，然后从二叉排序树中删去这个直接后继（或直接前驱），这样就转换成了第一或第二种情况。
例子
对于上述2，如果要删除60，我们发现它只有一个右子树，所以只需要把63替换到它位置就行
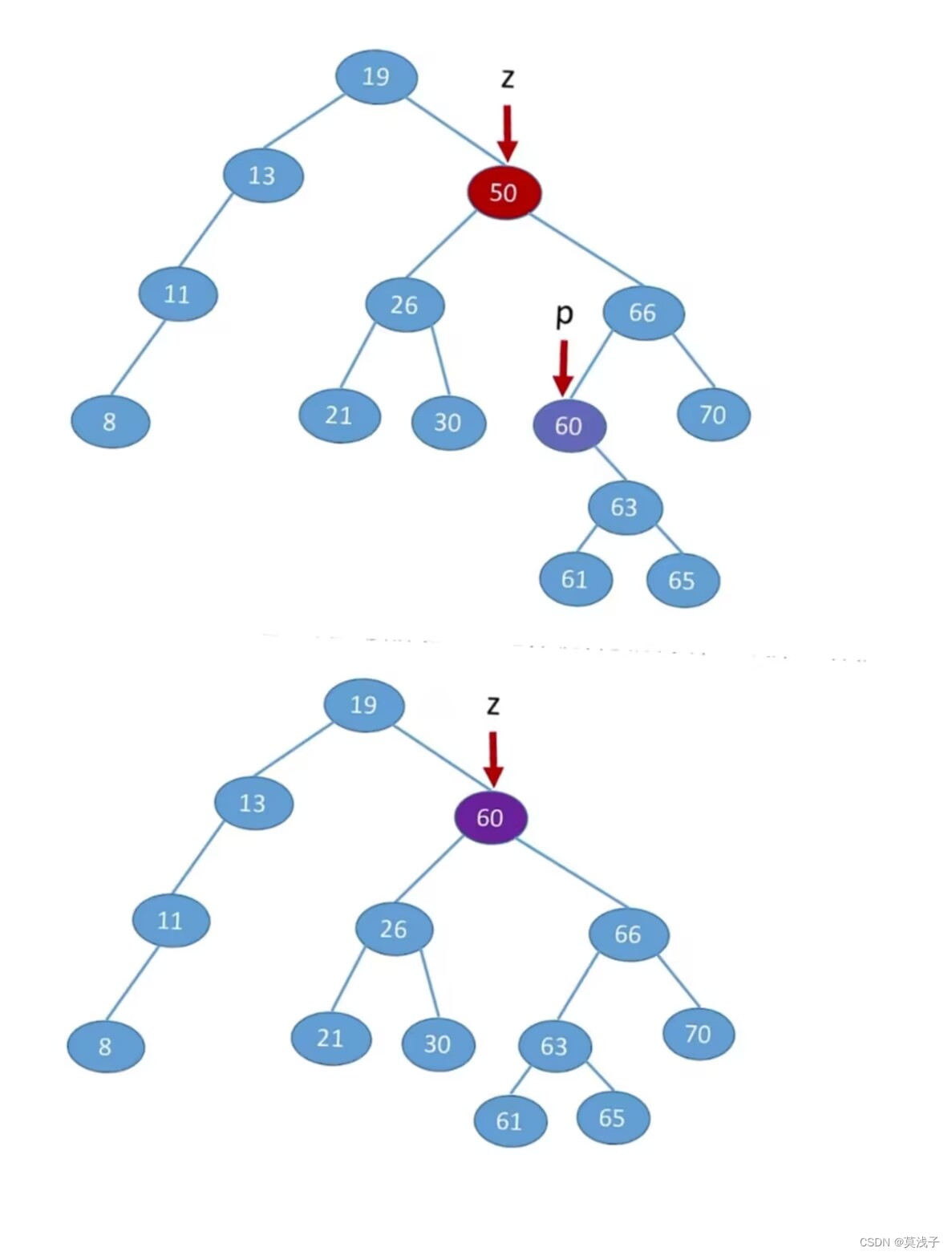
对于第三个，删除60这个结点我们发现，60有左右子树，所以我们可以先利用中序排序找到第一个访问的结点（其实就是最小的结点）然后删除50，想办法把60替换上去，其实就是删除60，删除60，我们发现它只有右子树，按照上面的方法（删除只有一棵左子树或右子树的方法），即可做到，如下图
也可以用当前左子树中最大的值，即是30，所以我们把60替换掉，取代60的位置就行，道理如
上 。
查找时间效率分析
查找长度——在查找运算中，需要对比关键字的次数称为查找长度，反应查找操作时间复杂度
查找成功的平均查找长度
查找失败的平均查找长度
- 点赞
- 收藏
- 关注作者
评论（0）