@TOC

图的定义及相关术语

• 图的定义：V表示由顶点的有穷非空集合，E表示顶点之间边的集合，则图G由V和E组成，记为G = (V, E)。其中顶点集V一定非空，边集可以为空。|V|表示图G中顶点的个数，|E|表示图G中边的条数。
• 相关术语：
  （1）有向图： 若E是有向边（弧）的有限集合时，则图G为有向图。<v, w>表示从v到w的一条弧，其中v, w是顶点，v称为弧尾，w称为弧头。
  
  （2）无向图：若E是无向边（边）的有限集合时，则图G为无向图。（v, w）表示v和w之间的一条边，其中v, w为顶点，（v, w）= （w, v）。
  
  （3）简单图：满足不存在重复边，不存在顶点到自身的边的图
  （4）完全图：对于无向图，|E|的取值范围是0到n(n-1)/2，有n(n-1)/2条边的无向图称为完全图（任意两个顶点之间都存在边）；对于有向图|E|的取值范围是0到n(n-1)，有n(n-1)条边的有向图称为有向完全图（任意两个顶点之间都存在方向相反的两条弧）。
  （5）稠密图、稀疏图：有很少条边或弧的图（如|E| < |V|log|V|）称为稀疏图，反之称为稠密图。
  （6）权、网：在一个图中，每条边都可以标上具有某种含义的数值，该数值称为该边的权值。这种带权的图称为带权图，也称网。
  （7）连通、连通图和连通分量：在无向图中，若从顶点v到w有路径存在，则称v和w是连通的。若G中任意两个顶点都是连通的，则G为连通图。无向图中的极大连通子图称为连通分量。
  （8）强连通、强连通图和强连通分量：在有向图中，若从顶点v到w和从顶点w到v之间都有路径，则称v和w是强连通的。若图中任意两个顶点都是强连通的，则称该图为强连通图。有向图中的极大强连通子图称为强连通分量。
  （9）生成树、生成森林：连通图的生成树是包含图中全部顶点的一个极小连通子图。在非连通图中，连通分量的生成树构成了非连通图的生成森林。
  （10）度、出度和入度：和顶点v相关联的边的数目称为v的度。对于有向图，以顶点v为头的弧的数目，称为v的入度；以顶点v为尾的弧的数目，称为v的出度。
  （11）简单路径：顶点不重复出现的路径，称为简单路径。
  （12）路径长度、距离：路径上边的数目称为路径长度。从顶点v到w的最短路径若存在，则此路径的长度称为v到w的距离。
  （13）有向树：一个顶点的入度为0，其余顶点的入度均为1的有向图，称为有向树。

图的存储结构

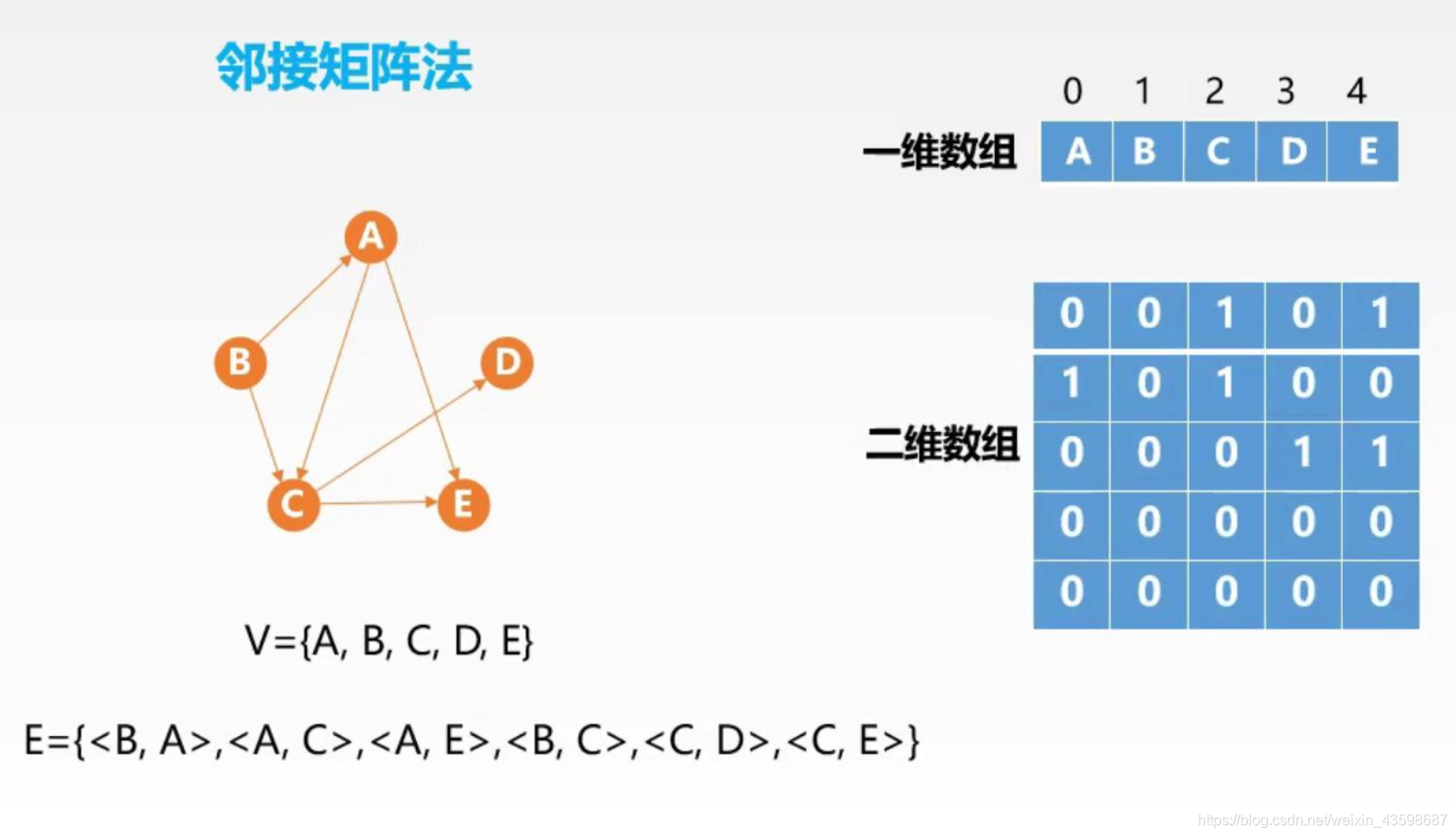
邻接矩阵法

用两个数组分别存储数据元素（顶点）的信息（一维数组）和数据元素之间的关系（边或弧）的信息（二维数组）。

#define MaxVNum 100			//最大顶点数
typedef struct{
	VType V[MaxVNum ];		//顶点表
	EType E[MaxVNum ][MaxVNum ];		//领接矩阵，边表
	int vnum, arcnum;		//当前顶点数和弧数
}Graph;

邻接矩阵具有以下特点：

• 无向图的邻接矩阵一定是一个对称矩阵；
• 在无向图中，邻接矩阵的第i行（或第i列）非零元素的个数就是第i个顶点的度；
• 在有向图中，邻接矩阵的第i行非零元素的个数就是第i个顶点的出度；邻接矩阵的第i列非零元素的个数就是第i个顶点的入度；
• 邻接矩阵法适合存储稠密图；
• 若A为图G的邻接矩阵，则A^n^的元素A^n^[i][j]等于由顶点i到j的长度为n的路径的数目。

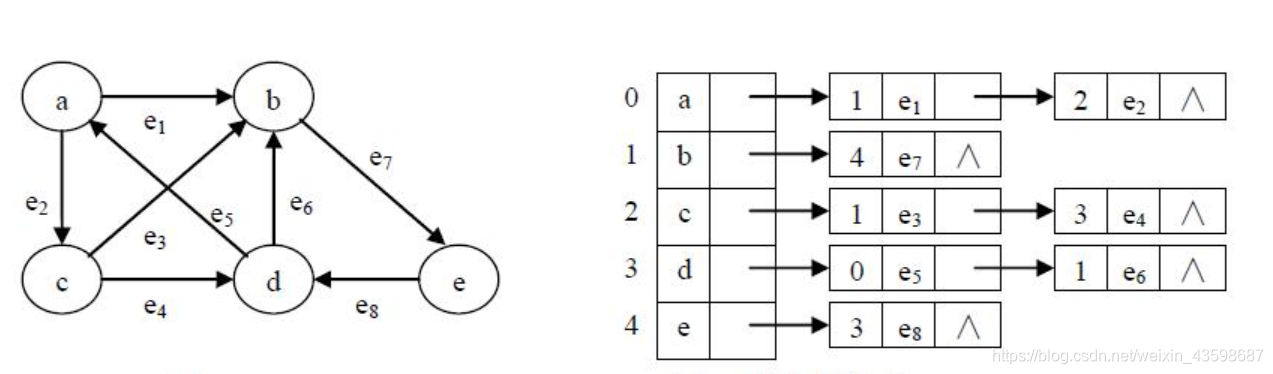
邻接表法

邻接表是指对图G中的每个顶点v~i~建立一个单链表，第i个单链表中的结点表示依附于顶点v~i~ 的边(对于有向图则是以顶点以为尾的弧)，这个单链表就称为顶点v~i~的边表(对于有向图则称为出边表)。边表的头指针和项点的数据信息采用顺序存储(称为顶点表)，所以在邻接表中存在两种结点：顶点表结点和边表结点。

顶点表结点由项点域(data)和指向第一条邻接边的指针(firstarc) 构成，边表(邻接
表)结点由邻接点域(adjvex)和指向下一条邻接边的指针域(nextarc) 构成。

#define MaxVNum 100			//最大顶点数
typedef struct ENode{		//边表节点
	int adjvex;				//该弧所指向的顶点的位置
	struct ENode *next;		//指向下一条弧的指针
}ENode;

typedef struct VNode{		//顶点表节点
	VType data;				//顶点信息
	ENode *first;			//指向第一条依附该顶点的弧的指针
}VNode,AdjList[MaxVNum];

typedef struct{
	AdjList vertices;		//邻接表
	int vnum, arcnum;		//当前顶点数和弧数
}Graph;

邻接表具有以下特点：

• 邻接表适合存储稀疏图；
• 图的邻接表表示并不唯一，因为在每个顶点对应的单链表中，各边结点的链接次序可以是任意的，它取决于建立邻接表的算法及边的输入次序；
• 在有向图的邻接表表示中，一个给定顶点的出度等于其邻接表中的结点个数；

十字链表

十字链表是有向图的一种链式存储结构。在十字链表中，对应于有向图中每一条弧有一个节点，对应于每个顶点也有一个节点。
弧结点中有5个域:尾域(tailvex) 和头域(headvex) 分别指示弧尾和弧头这两个顶点在图中的位置；链域hlink指向弧头相同的下一条弧；链域tlink指向弧尾相同的下一条弧；info域指向该弧的相关信息。这样，弧头相同的弧就在同一个链表上，弧尾相同的弧也在同一个链表上。
顶点结点中有3个域：data域存放顶点相关的数据信息，如顶点名称；firstin和firstout两个域分别指向以该顶点为弧头或弧尾的第一个弧结点。

#define MaxVNum 100			//最大顶点数
typedef struct ENode{		//边表节点
	int tailvex,headvex;	//该弧的尾和头顶点的位置
	struct ENode *hlink,*tlink;		//分别为弧头相同和弧尾相同的弧的链域
	InfoType *info;			//该弧相关信息的指针
}ENode;

typedef struct VNode{		//顶点表节点
	VType data;				//顶点信息
	ENode *firstin,*firstout;			//分别指向该顶点的入弧和出弧
}VNode;

typedef struct{
	VNode xlist[MaxVNum];	//表头向量
	int vnum, arcnum;		//当前顶点数和弧数
}Graph;

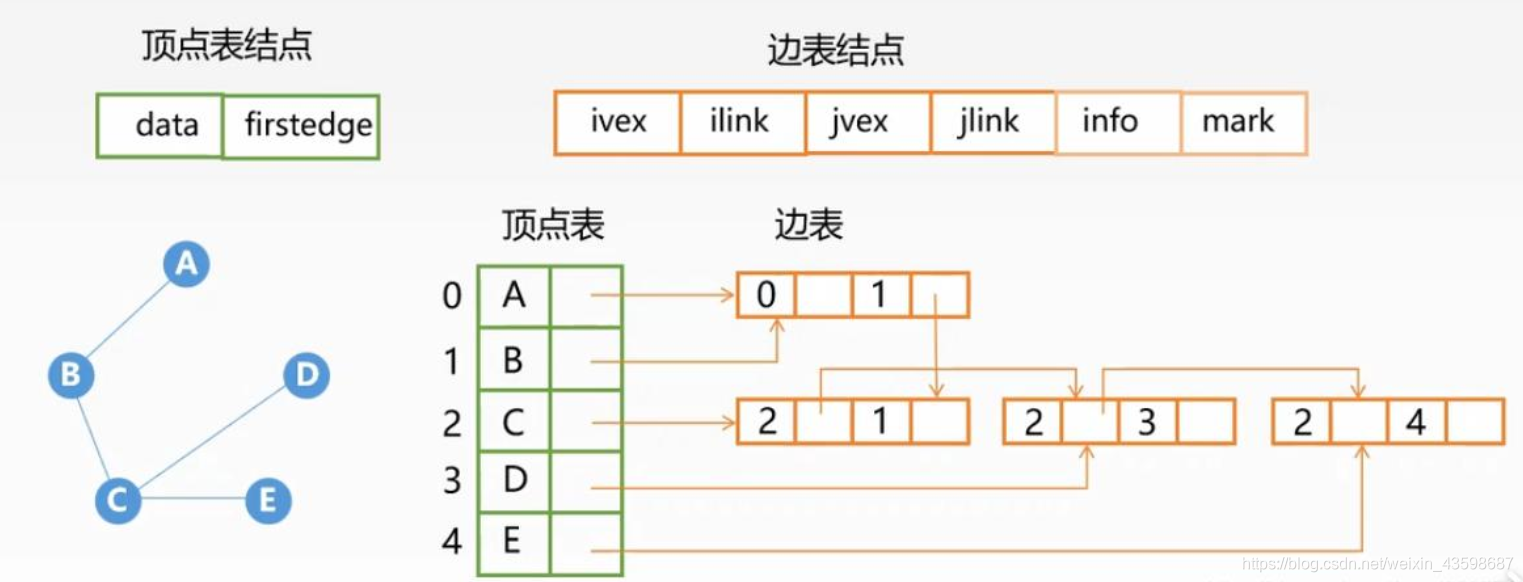
邻接多重表

邻接多重表是无向图的一种链式存储结构。
与十字链表类似，在邻接多重表中，每条边用一个结点表示。其中，mark为标志域，可用以标记该条边是否被搜索过; ivex和jvex为该边依附的两个顶点在图中的位置; ilink 指向下一条依附于顶点ivex的边; jlink 指向下一条依附于顶点jvex的边，info 为指向和边相关的各种信息的指针域。
每个顶点也用一个结点表示，其中，data域存储该顶点的相关信息，firstedge域指示第一条依附于该顶点的边。

#define MaxVNum 100			//最大顶点数
typedef struct ENode{		//边表节点
	int mark;				//访问标记
	int ivex,jvex;			//该边依附的两个顶点的位置
	struct ENode *ilink,*jlink;		//分别指向依附这两个顶点的下一条边
	InfoType *info;			//该边相关信息的指针
}ENode;

typedef struct VNode{		//顶点表节点
	VType data;				//顶点信息
	ENode *firstedge;		//指向第一条依附该顶点的边
}VNode;

typedef struct{
	VNode xlist[MaxVNum];
	int vnum, edgenum;		//当前顶点数和弧数
}Graph;