Python数学基础二、利用正弦sin求曲边图形的面积

​

目录

正弦

求曲边图形的面积

推导方式解法：

推导式解法：

正弦

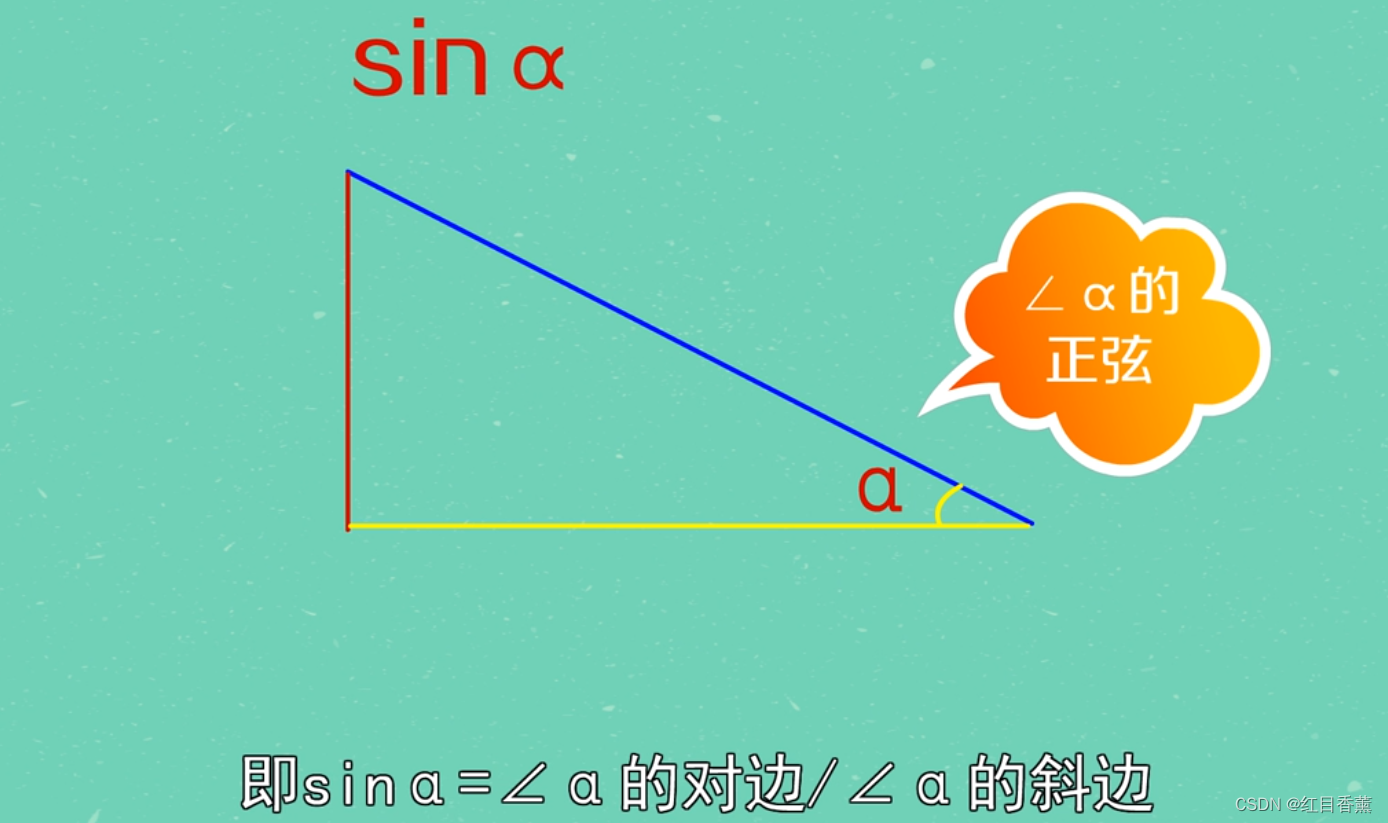
古代的勾三股四弦五中说的弦就是我们要说的正弦，也就是直角三角形中的斜边，叫做弦，股就是人的大腿，古人称直角三角形长的那个直角边就叫做股。

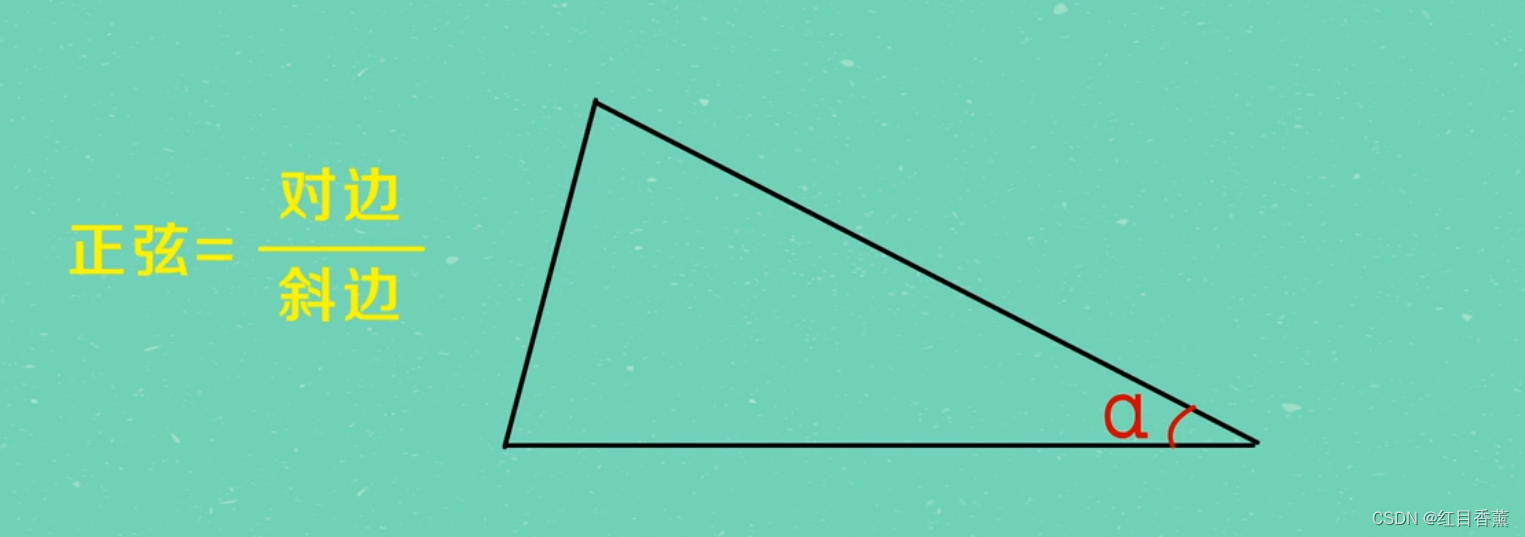
正弦是∠α的对边/斜边的比。

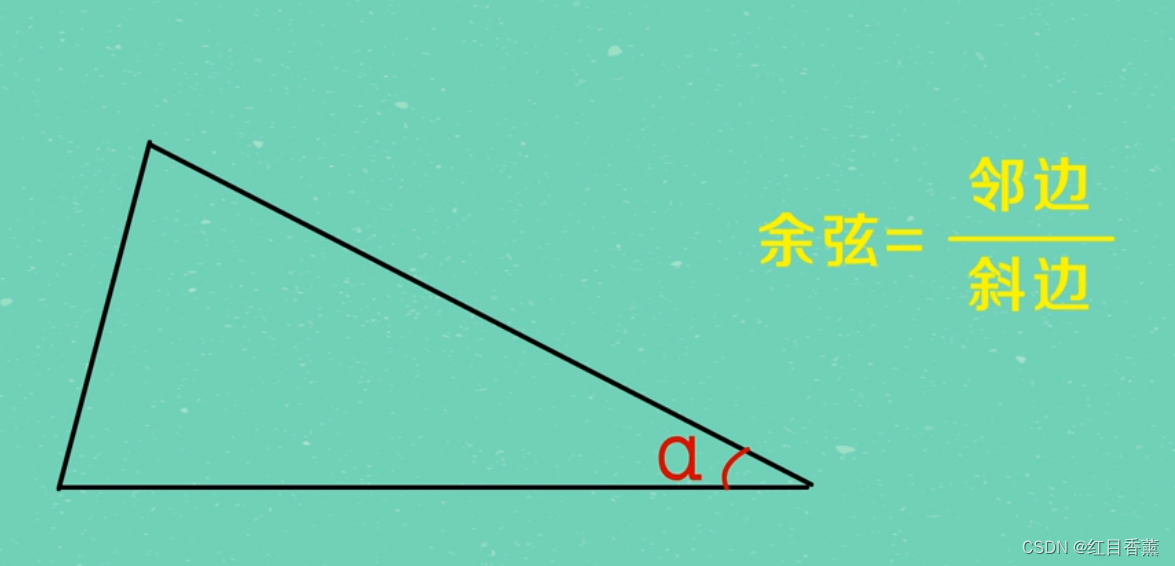
余弦是邻边/斜边的比

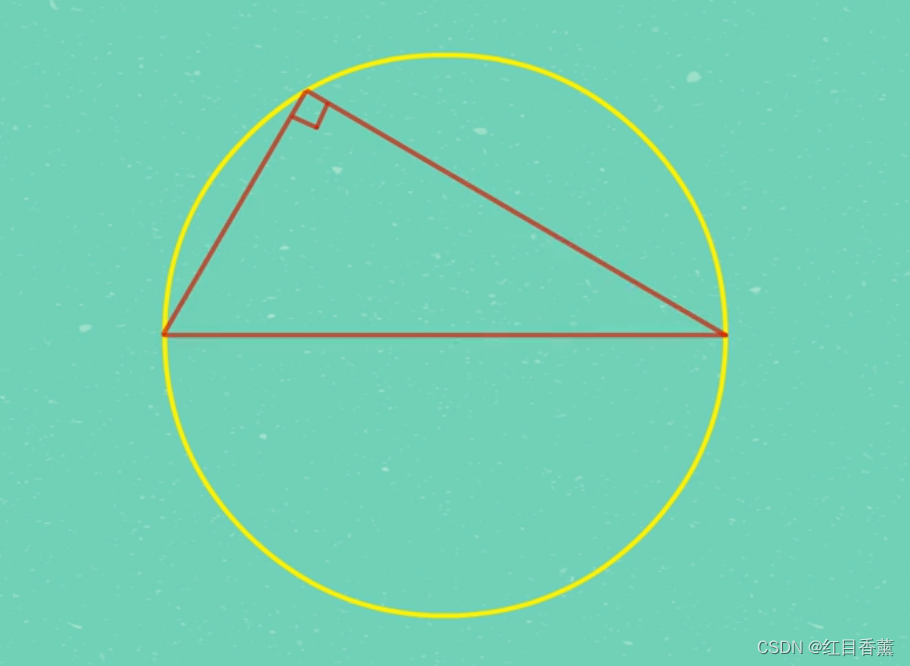
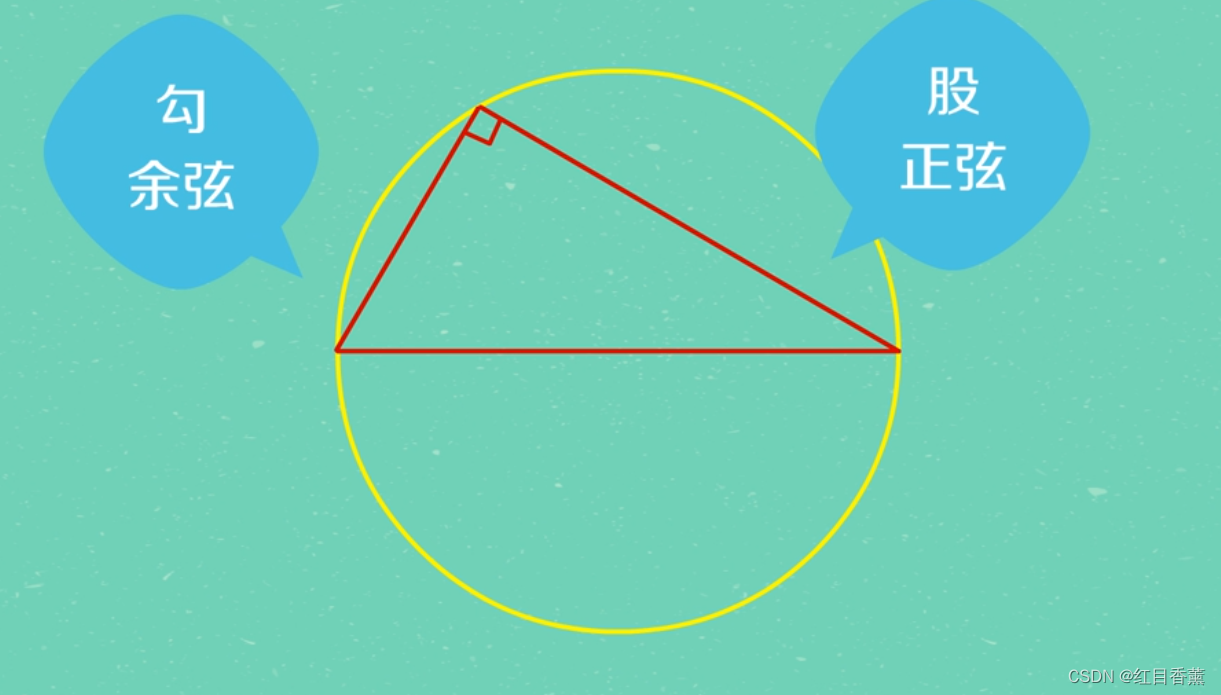
如果把勾股弦放在一个圆里面，弦就是圆上两个点的连线，最大的正弦值就是圆的直径。

这个图也能明显的看出来，勾股弦之间的关系。

∠α的正弦=对边/斜边

我们确定正弦是什么后，我们来计算下面的这个题目：

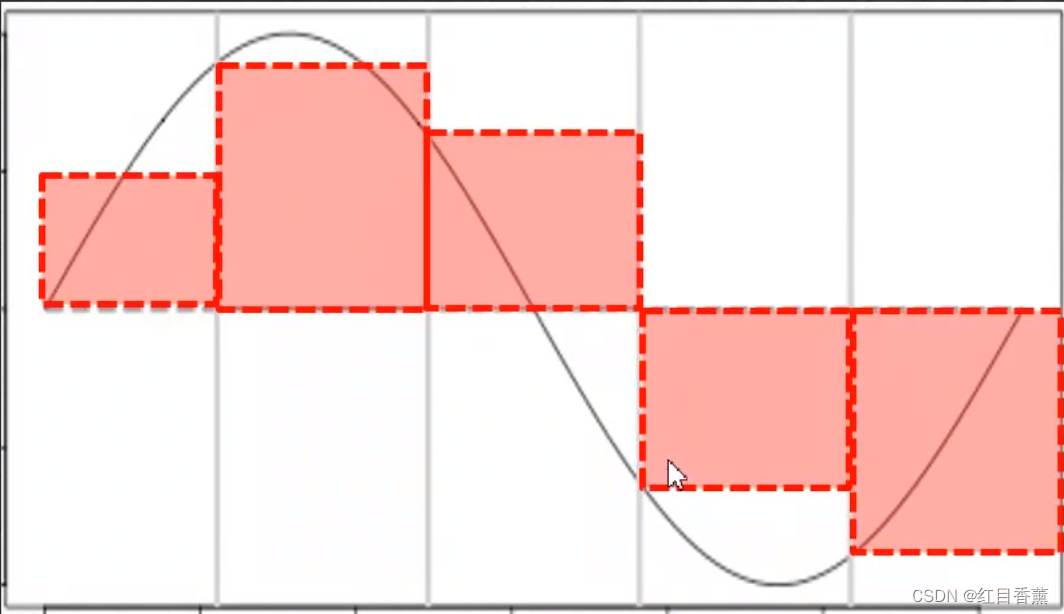
求曲边图形的面积

求y=sin(x)从0到2* pi，与x轴围成的面积。

步骤分析：
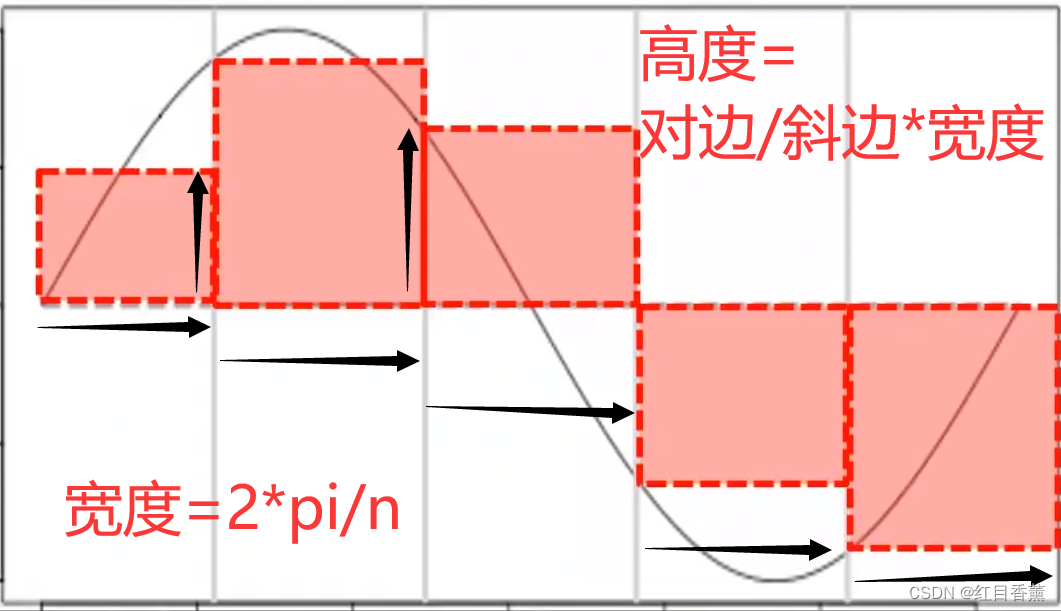
1.将各小矩形的高度存放至一列表中。

高度=正弦值的绝对值=对边/斜边*宽度
2.将各高度乘以宽度，得各矩形面积。这里可以分为无数的小矩形。

小矩形面积=高度*宽度
3.求和。

sum(叫矩形面积数组)

推导方式解法：

# 求曲边图形的面积
import math

# 先拆分10个简单算一下。不精确
n = 10
# 每个宽度=2*pi/n
width = 2 * math.pi / n
# 宽度数组
x = []
# 把x轴每次延伸的值逐一放进去
for i in range(n):
    x.append((i * width))
# 高度数组
y = []
# 遍历宽度，根据高度=正弦的绝对值，由于是正弦肯定有正负，那么我们就计算一下绝对值。
for i in x:
    y.append(abs(math.sin(i)))
# 求和
S = sum(y) * width
print(S)

推导式解法：

# 求曲边图形的面积
import math

# 先拆分10个简单算一下。不精确
n = 10
# 每个宽度=2*pi/n
width = 2 * math.pi / n
# 推导式
s = [abs(math.sin(i * width)) * width for i in range(n)]
print(sum(s))

这个小题还是有些麻烦的，理解起来还是没那么容易的。我们看第一个解决方案还是相对理解起来比较容易的，第二个推导式就不是太容易理解的。我们需要对Python的语法非常了解，再加上对题目的理解来搞定这个题目。

如果对于第二个方法难以理解的话可以看后面的博客文章，我会在下一篇文章对这块进行一个深度的讲解。

​