二叉树最大宽度&&后继者
【摘要】 662. 二叉树最大宽度https://leetcode.cn/problems/maximum-width-of-binary-tree/从题可以得知:本题的层数从1开始,根节点是第一层空节点也被算进长度中,所以普通的层序遍历不能解决问题,每个节点原本的值是没有用处的,所以我们可以用其来保存节点的位置信息对于一颗完全二叉树,如果按照从上至下,从左往右对所有节点从零开始顺序编号则父节点的左...
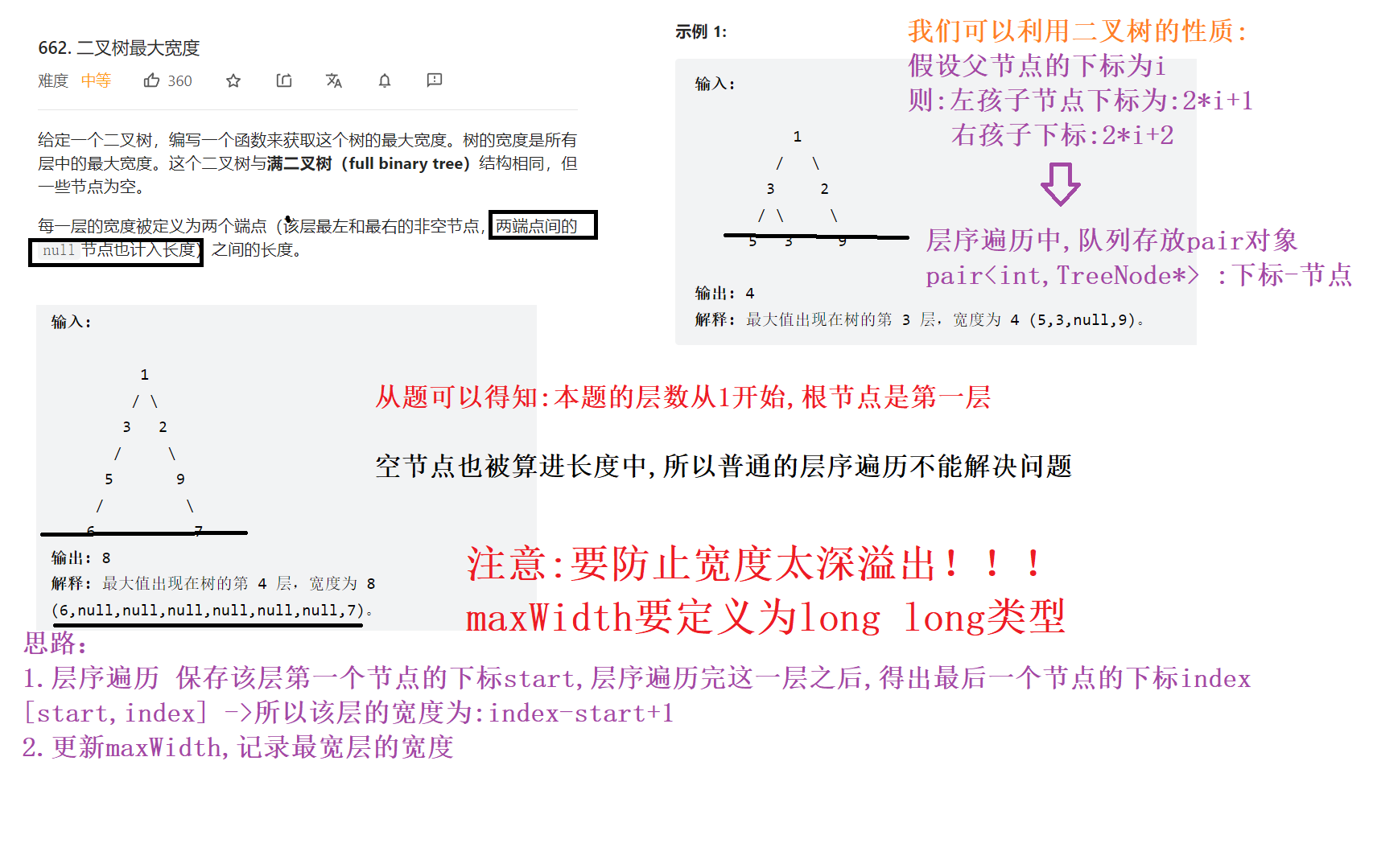
662. 二叉树最大宽度
从题可以得知:本题的层数从1开始,根节点是第一层
空节点也被算进长度中,所以普通的层序遍历不能解决问题,每个节点原本的值是没有用处的,所以我们可以用其来保存节点的位置信息
对于一颗完全二叉树,如果按照从上至下,从左往右对所有节点从零开始顺序编号则父节点的左孩子节点的序号:2*i+1 父节点的左孩子节点的序号:2*i+2;所以每层的宽度就可以使用:每层最后一个节点的值减去最后一个节点的值+1
层序遍历中,队列存放pair对象 pair<int,TreeNode*> :下标-节点
思路:
- 层序遍历 保存该层第一个节点的下标start,层序遍历完这一层之后,得出最后一个节点的下标index
[start,index] ->所以该层的宽度为:index-start+1 - 更新maxWidth,记录最宽层的宽度
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
//如果不改成long long类型会过不了!
/*
[0,0,0,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null,null,0,0,null]
*/
class Solution {
public:
int widthOfBinaryTree(TreeNode* root) {
if(root == nullptr) return 0;
//队列存放的是pari对象
//第一个成员代表:该节点所在数组的下标 第二个成员:节点
queue<pair<int,TreeNode*>> q;
q.push(make_pair(1,root));//根节点在下标为1位置
long long maxWidth = 0;//最大宽度
while(!q.empty())
{
long long start = q.front().first;//这一层第一个节点的起始下标位置
long long index = 0;//标志当前节点的下标,其左孩子下标:index*2+1 右孩子:index*2+2
long long size = q.size();//这一层有多少个节点
//处理这一层的节点
for(int i = 0;i<size;i++)
{
pair<int,TreeNode*> tmp = q.front();//队头元素
q.pop();
//tmp是pair对象
//tmp.first -> 该节点所在下标 tmp->second ->节点
index = tmp.first;//拿到当前节点的下标
//处理左右孩子
if(tmp.second->left != nullptr)
{
q.push(make_pair(index*2+1,tmp.second->left));
}
if(tmp.second->right !=nullptr)
{
q.push(make_pair(index*2+2,tmp.second->right));
}
}
//更新最大宽度
//start为当前层的第一个节点的下标位置 index为当前层最后一个节点的下标
//当前层的宽度为: index - start+1 [start,index]
maxWidth = max(maxWidth,index - start+1);
}
return maxWidth;
}
};
面试题 04.06. 后继者
题目也可以转化为求: 第一个比p->val值更大的节点
二叉搜索树,我们很自然的想到中序遍历 所以方法:走一遍中序遍历,找到第一个比p->val大的节点就返回该节点
非递归版本:
class Solution {
public:
TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p)
{
if(root == nullptr) return nullptr;
//找到中序遍历中第一个值大于p->val的节点
//非递归中序遍历
stack<TreeNode*> st;
TreeNode* cur = root;
TreeNode* ans = nullptr;//记录答案
while(!st.empty() || cur !=nullptr)
{
//先把左路节点全部入栈
while(cur)
{
st.push(cur);
cur = cur->left;
}
TreeNode* top = st.top();
st.pop();
//比较值是否大于p->val
//找到第一个比p->val大的节点就直接返回
if(top->val > p->val)
{
ans = top;
break;
}
//去右树访问
cur = top->right;
}
return ans;
}
};
递归版本:
去左树看看有没有比p->val的值大的节点 ,找到了就返回 没有就去右树找
答案不是在左树就是在右树
class Solution {
public:
TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
//我们要找的是第一个大于p->val的节点, 所以遇到第一个大于p->val的即可返回
if(root == nullptr) return nullptr;
TreeNode* res = inorderSuccessor(root->left,p); //在左树有没有找到答案
//左树返回不为空,说明res就是答案
if(res!=nullptr) return res;
//找到第一个大于p->val的节点
if(root->val > p->val)
return root;
//如果答案不是在左树就是在右树
return inorderSuccessor(root->right,p);
}
};
方法2:利用二叉搜索树的性质查找第一个比p->val大的节点
- 如果当前节点的值比p->val的值小:去右树中寻找
- 如果当前节点的值比p->val的值大:先记录当前节点,然后去左树继续找 (因为要找的是>p.val的所有节点的值最小的一个节点)
class Solution {
public:
TreeNode* inorderSuccessor(TreeNode* root, TreeNode* p) {
if(root == nullptr) return nullptr;
//求>p.val的所有节点的值最小的一个节点
int target = p->val;//目标值
TreeNode* cur = root;//从根节点开始找
TreeNode* ans = nullptr;//记录答案节点
while(cur)
{
if(cur->val > target)
{
ans = cur;
cur = cur->left;//继续去左树看有没有更合适的>p.val的较小值
}
else //cur->val < target 不可能取等于,因为是二叉搜索树
{
cur = cur->right;
}
}
return ans;
}
};
【声明】本内容来自华为云开发者社区博主,不代表华为云及华为云开发者社区的观点和立场。转载时必须标注文章的来源(华为云社区)、文章链接、文章作者等基本信息,否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)