左叶子之和&&从二叉搜索树到更大和树
【摘要】 404.左叶子之和https://leetcode.cn/problems/sum-of-left-leaves/1.根节点不累加到结果中2.注意理解这里的左叶子的含义:这个是所有左边的叶子节点,并不是最左的结点,所以并不能使用层序遍历去拿到第一个左边的结点3.我们不能判断当前节点是不是左叶子只能判断当前节点是不是叶子(当前节点左为空&&右为空)必须通过其父节点来判断其左孩子是不是左叶子条...
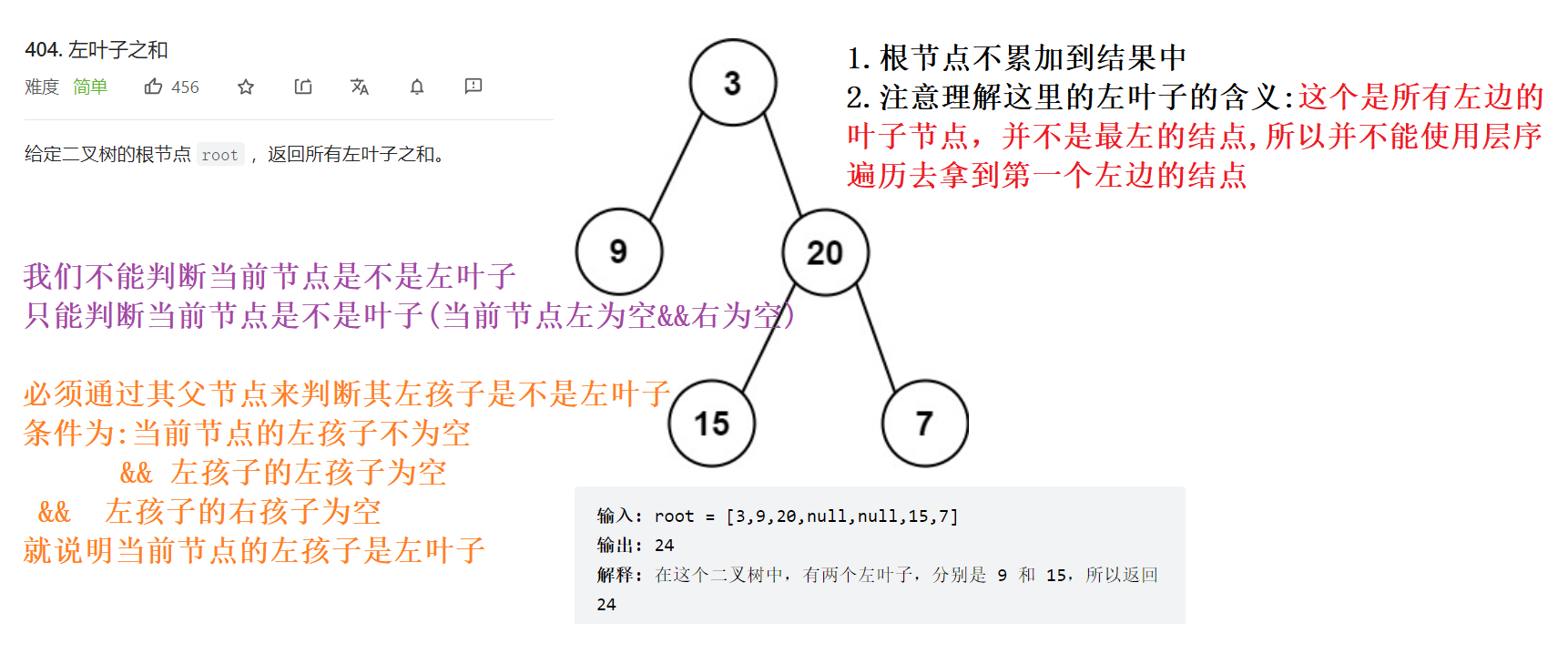
404.左叶子之和
1.根节点不累加到结果中
2.注意理解这里的左叶子的含义:这个是所有左边的叶子节点,并不是最左的结点,所以并不能使用层序遍历去拿到第一个左边的结点
3.我们不能判断当前节点是不是左叶子
- 只能判断当前节点是不是叶子(当前节点左为空&&右为空)
必须通过其父节点来判断其左孩子是不是左叶子
- 条件为:当前节点的左孩子不为空 && 左孩子的左孩子为空 && 左孩子的右孩子为空 就说明当前节点的左孩子是左叶子
遍历整个二叉树,判断是否为左叶子,如果是就累加到sum中
核心代码:通过当前节点判断它的左孩子是不是左叶子root->left && root->left->left == nullptr&& root->left->right == nullptr
- root->left !=nullptr 保证了当前节点有左孩子
- root->left->left == nullptr &&root->left->right == nullptr : 说明当前节点的左孩子没有孩子->是叶子节点->是左叶子
同理:判断是不是右叶子:root->right&& root->right->right== nullptr&& root->right->left== nullptr
- root->right!=nullptr 保证了当前节点有右孩子
- root->right->left == nullptr &&root->right->right== nullptr : 说明当前节点的右孩子没有孩子->是叶子节点->是右叶子
class Solution {
public:
int sum = 0;//统计左叶子的值的和,相当于是全局变量
int sumOfLeftLeaves(TreeNode* root) {
if(root == nullptr) return 0;
//问题所在:左叶子如何判断
//根据父亲判断比较好!
//如果当前节点的左孩子不为空 && 左孩子的左孩子为空 && 左孩子的右孩子为空 就说明当前节点的左孩子是左叶子
if(root->left && root->left->left == nullptr&& root->left->right == nullptr)
{
sum+=root->left->val;//累加当前节点的左孩子的值 (累加左叶子的值)
}
sumOfLeftLeaves(root->left);//去右树递归
sumOfLeftLeaves(root->right);//去左树递归
return sum;
}
};
1038. 从二叉搜索树到更大和树
https://leetcode.cn/problems/binary-search-tree-to-greater-sum-tree/
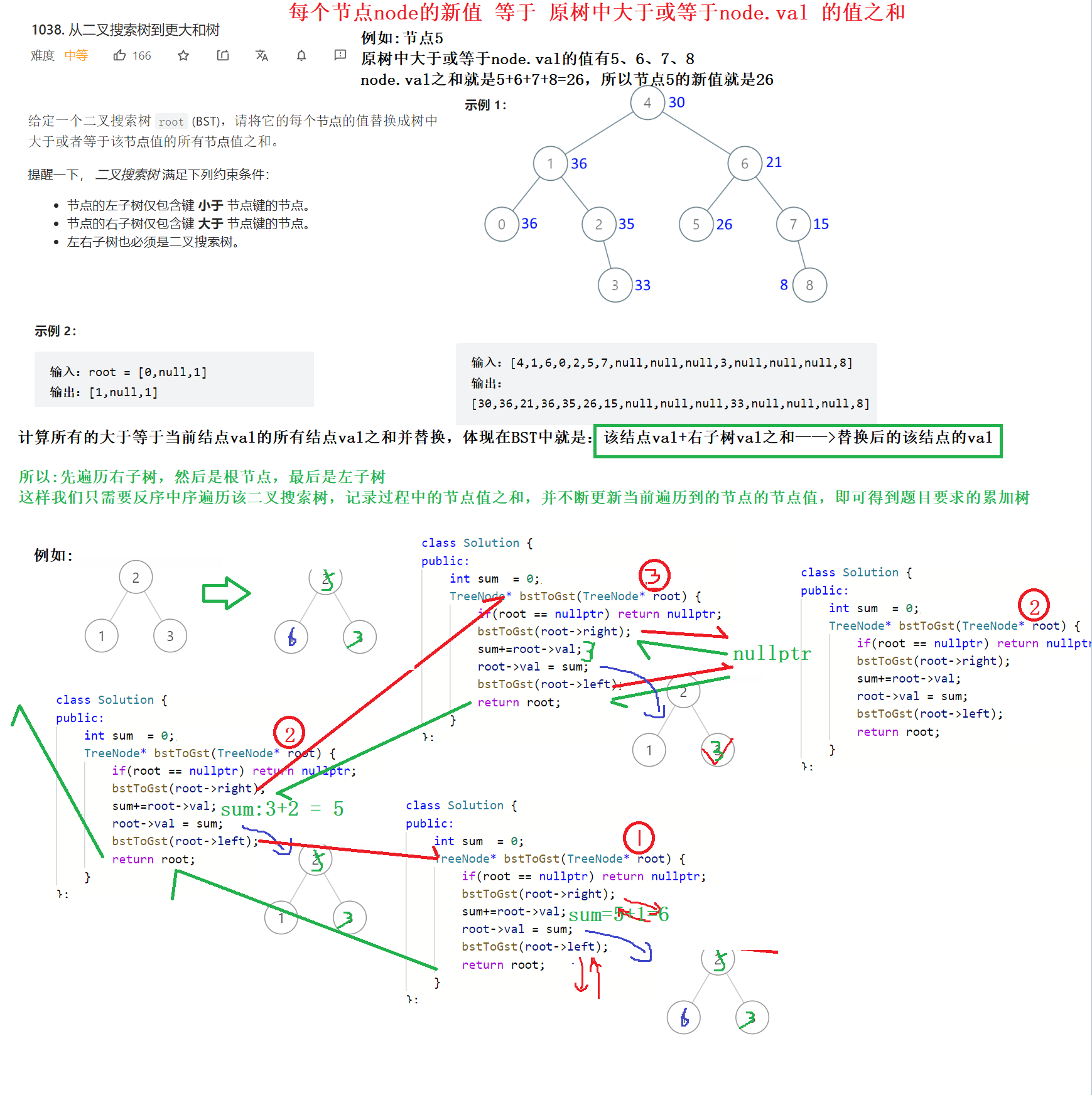
计算所有的大于等于当前结点val的所有结点val之和并替换,体现在BST中就是:该结点val+右子树val之和=>替换后的该结点的val
所以:先遍历右子树,然后是根节点,最后是左子树
这样我们只需要反序中序遍历该二叉搜索树,记录过程中的节点值之和,并不断更新当前遍历到的节点的节点值,即可得到题目要求的累加树
class Solution {
public:
int sum = 0;//记录过程中的节点值之和
TreeNode* bstToGst(TreeNode* root) {
//反向走中序
if(root == nullptr) return nullptr;
bstToGst(root->right);//先递归右树
//处理
sum+=root->val;//sum累加当前节点的值 该节点的值 + 右子树的值->替换后的val
root->val = sum;//更新节点的值为sum
bstToGst(root->left);//递归左树
return root;
}
};
【声明】本内容来自华为云开发者社区博主,不代表华为云及华为云开发者社区的观点和立场。转载时必须标注文章的来源(华为云社区)、文章链接、文章作者等基本信息,否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容,欢迎发送邮件进行举报,并提供相关证据,一经查实,本社区将立刻删除涉嫌侵权内容,举报邮箱:
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者


评论(0)