⭐️【强化完全背包练习】完全背包原题⭐️

🔐题目详情

279. 完全平方数

难度中等

给你一个整数 n ，返回 和为 n 的完全平方数的最少数量 。

完全平方数 是一个整数，其值等于另一个整数的平方；换句话说，其值等于一个整数自乘的积。例如，1、4、9 和 16 都是完全平方数，而 3 和 11 不是。

示例 1：

输入：n = 12
输出：3 
解释：12 = 4 + 4 + 4

示例 2：

输入：n = 13
输出：2
解释：13 = 4 + 9

提示：

• 1 <= n <= 104

💡解题思路与代码

🍭朴素解法

我们分析一下，本题的意思是从不大于n的完全平方数中选择若干数凑成n，求凑成数n的最小数量。

那这道题就是一道完全背包问题，即背包中的【物品】就是不大于n的完全平方数，每件物品的价值可以理解为1，每件物品体积可以理解为数字的值，每个物品可以选择无数次 ，求凑成数n的所选择物品的最小数量（即凑出总体积恰好为n时的物品最低价值）。

状态定义： 不妨定义 $f[i][j]$表示从前 $i$件物品中选择，恰好凑成 $j$，所选物品的最小数量，任何数都是1的倍数，所以不存在无法凑出的情况。

确定初始状态： 当 $i=0$时，只能选择物品【1】，因为 $1$可以被任何正整数整除，所以 $f[0][j]=j/1$。

状态转移方程推导： 当我们选择第 $i$件物品的时候，我们可以选择 $0,1,2...k$件，其中 $k$是最大能够选择的件数，即在恰好凑出 $j$的情况下。
假设第 $i$件物品的数值【体积】为 $t$。
当我们不选择第 $i$件物品时，即 $k=0$， $f[i][j]=f[i-1][j]$。
当我们选择 $1$件第 $i$件物品时，即 $k=1$， $f[i][j]=f[i-1][j - t] + 1$。
当我们选择 $2$件第 $i$件物品时，即 $k=2$， $f[i][j]=f[i-1][j - 2 * t] + 2$。
…
当我们选择 $k$件第 $i$件物品时，即 $k=k$， $f[i][j]=f[i-1][j - k * t]+k$。

我们所要求的是最小平方数的数量值，所以取以上所有情况的最小值即可。

综上所述，我们的状态转移方程就出来了，不妨记当前物品的价值为：

$$f[i][j]=max(f[i-1][j-k*t]+k),k=0,1,...$$

实现代码：

class Solution {
    public int numSquares(int n) {
        //动态规划 完全背包问题
        //1.枚举1-n之间所有的完全平方数
        int len = (int) Math.sqrt(n);
        int[] nums = new int[n];
        for (int i = 1; i * i <= n; i++) {
            nums[i - 1] = i * i;
        }

        //状态定义f[i][j]表示和为n完全平方和的最小数量

        int[][] f = new int[len][n + 1];

        //确定初始状态，处理只有一个数字时
        for (int j = 1; j <= n; j++) {
            int k = j / nums[0];
            //由于第一个数字是1 大于1的整数一定能够被1整除，所以判断是否为1的倍数可以省略
            f[0][j] = k;
        }

        //状态转移
        for (int i = 1; i < len; i++) {
            int t = nums[i];
            for (int j = 1; j <= n; j++) {
                //不选
                f[i][j] = f[i - 1][j];
                //选择k个
                for (int k = 1; k * t <= j; k++) {
                    f[i][j] = Math.min(f[i][j], f[i - 1][j - k * t] + k);
                }
            }
        }
        return f[len - 1][n];
    }
}

时间复杂度： $O(n^2*len)$， $k$的值不会大于 $n$，因为 $t$最小为 $1$，最多选择的数的数量不会超过 $n$。
空间复杂度： $O(n*len)$

🍭滚动数组优化空间

根据观察我们知道第 $i$行的状态仅依赖与第 $i-1$行的状态，因此我们可以使用滚动数组进行优化。

实现代码：

class Solution {
    public int numSquares(int n) {
        //动态规划 完全背包问题
        //1.枚举1-n之间所有的完全平方数
        int len = (int) Math.sqrt(n);
        int[] nums = new int[n];
        for (int i = 1; i * i <= n; i++) {
            nums[i - 1] = i * i;
        }

        //状态定义f[i][j]表示和为n完全平方和的最小数量

        int[][] f = new int[2][n + 1];

        //确定初始状态，处理只有一个数字时
        for (int j = 1; j <= n; j++) {
            int k = j / nums[0];
            //由于第一个数字是1 大于1的整数一定能够被1整除，所以判断是否为1的倍数可以省略
            f[0][j] = k;
        }

        //状态转移
        for (int i = 1; i < len; i++) {
            int t = nums[i];
            int cur = i & 1;
            int pre = (i - 1) & 1;
            for (int j = 1; j <= n; j++) {
                //不选
                f[cur][j] = f[pre][j];
                //选择k个
                for (int k = 1; k * t <= j; k++) {
                    f[cur][j] = Math.min(f[cur][j], f[pre][j - k * t] + k);
                }
            }
        }
        return f[(len - 1) & 1][n];
    }
}

对于时空复杂度，只是优化了空间而已，所以时间复杂度不发生改变，空间复杂度优化到 $O(n)$。
时间复杂度： $O(n^2*len)$， $k$的值不会大于 $n$，因为 $t$最小为 $1$，最多选择的数的数量不会超过 $n$。
空间复杂度： $O(n)$

🍭一维数组优化空间

首先我们对状态转移方程进行一个简单的推导：

$$f[i][j]=min(f[i-1][j],f[i-1][j-t]+1,f[i-1][j-2*t]+2,...,f[i-1][j-kt]+k)$$

$$f[i][j-t]=min(f[i-1][j-t],f[i-1][j-2t]+1,f[i-1][j-3t]+2...,f[i-1][j-kt]+k-1)$$

其中 $k*t<=j$。

通过观察上面两个状态的式子，我们发现后面一部分式子是差了一个 $1$如下图：

所以我们可以进一步优化状态转移方程，即：

$$f[i][j]=min(f[i-1][j],f[i][j-t]+1)$$

对于新推导出来的状态转移方程，它的状态转移仅仅只依赖与上一行同列状态与同一行元素前面的元素，所以我们可以将原来的二维数组优化为一维，由于它只依赖左边与正上方的元素，我们可以采取从小到大遍历背包容量状态来求背包中所放物品最大值。

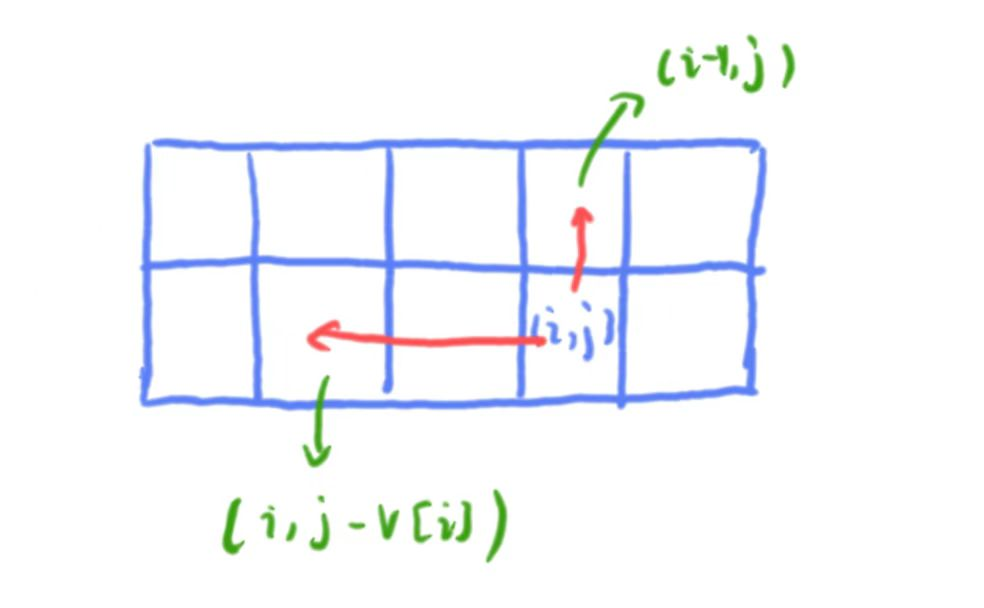
只保留【凑出数字值】维度，状态转移方程为：

$$f[j]=max(f[j],f[j-t]+1)$$

实现代码：

class Solution {
    public int numSquares(int n) {
        //动态规划 完全背包问题
        //1.枚举1-n之间所有的完全平方数
        int len = (int) Math.sqrt(n);
        int[] nums = new int[n];
        for (int i = 1; i * i <= n; i++) {
            nums[i - 1] = i * i;
        }

        //状态定义f[j]表示和为n完全平方和的最小数量

        int[] f = new int[n + 1];

        //确定初始状态，处理只有一个数字时
        for (int j = 1; j <= n; j++) {
            int k = j / nums[0];
            //由于第一个数字是1 大于1的整数一定能够被1整除，所以判断是否为1的倍数可以省略
            f[j] = k;
        }

        //状态转移
        for (int i = 1; i < len; i++) {
            int t = nums[i];
            for (int j = t; j <= n; j++) {
                //f[j]=min(f[j], f[j-t]+1)

                f[j] = Math.min(f[j], f[j - t] + 1);
            }
        }
        return f[n];
    }
}

时间复杂度： $O(len*n)$
空间复杂度： $O(n+1)$

🌱总结

本篇文章介绍了【完全背包】的运用，使用该模型运用到实际的问题当中，强化一维优化过程的推导。

对于完全背包的优化，相比于0-1背包问题的优化，形式上，我们只需要将 01 背包问题的「一维空间优化」解法中的「容量维度」遍历方向从「从大到小 改为 从小到大」就可以解决完全背包问题。
但本质是因为两者进行状态转移时依赖了不同的格子：
0 -1 背包依赖的是「上一行正上方的格子」和「上一行左边的格子」。
完全背包依赖的是「上一行正上方的格子」和「本行左边的格子」。

参考资料： 宫水三叶背包问题