⭐️左右最值最大差⭐️

🔐题目详情

给定一个长度为N(N>1)的整型数组A，可以将A划分成左右两个部分，左部分A[0…K]，右部分A[K+1…N-1]，K可以取值的范围是[0,N-2]。求这么多划分方案中，左部分中的最大值减去右部分最大值的绝对值，最大是多少？

给定整数数组A和数组的大小n，请返回题目所求的答案。

测试样例：

[2,7,3,1,1],5
返回：6

链接：左右最值最大差
来源：牛客网

💡解题思路

基本思路： 数学
解题思路：

左边部分至少包含arr[0]，右边部分至少包含arr[n-1]，也就是说左边的最大值至少为arr[0]，右边的最大值至少为arr[n - 1]，并且整个数组的最大值不是分在左边就是分在右边，当一边最大值为arr[0]与arr[n - 1]较小一个，另一边最大值为数组最大值时，此时两边的最大值差的绝对值最大，因此左边与右边最大的绝对值差为max-min(arr[0], arr[1])。

🔑源代码

import java.util.*;

public class MaxGap {
    public int findMaxGap(int[] arr, int n) {
        // write code here
        int max = 0;
        for (int i = 0; i < n; i++) {
            if (arr[i] > max) max = arr[i];
        }
        //左区间至少包含arr[0]，右区间至少包含arr[n - 1]
        //两边最大值之差最大为数组最大值减去两个端点的最小值
        return max - Math.min(arr[0], arr[n - 1]);
    }
}

🌱总结

本题为数学推理题。

⭐️顺时针打印矩阵⭐️

🔐题目详情

对于一个矩阵，请设计一个算法从左上角(mat[0][0])开始，顺时针打印矩阵元素。

给定int矩阵mat,以及它的维数nxm，请返回一个数组，数组中的元素为矩阵元素的顺时针输出。

测试样例：

[[1,2],[3,4]],2,2
返回：[1,2,4,3]

链接：顺时针打印矩阵
来源：牛客网

💡解题思路

基本思路： 模拟

解题思路：
第一步，打印顶行。
第二步，打印右列。
第三步，打印底行。
第四步，打印左列。

每一步都需要验证，左列序号是否大于右列序号或顶行序号是否大于底行序号，如果是，需要终止循环。

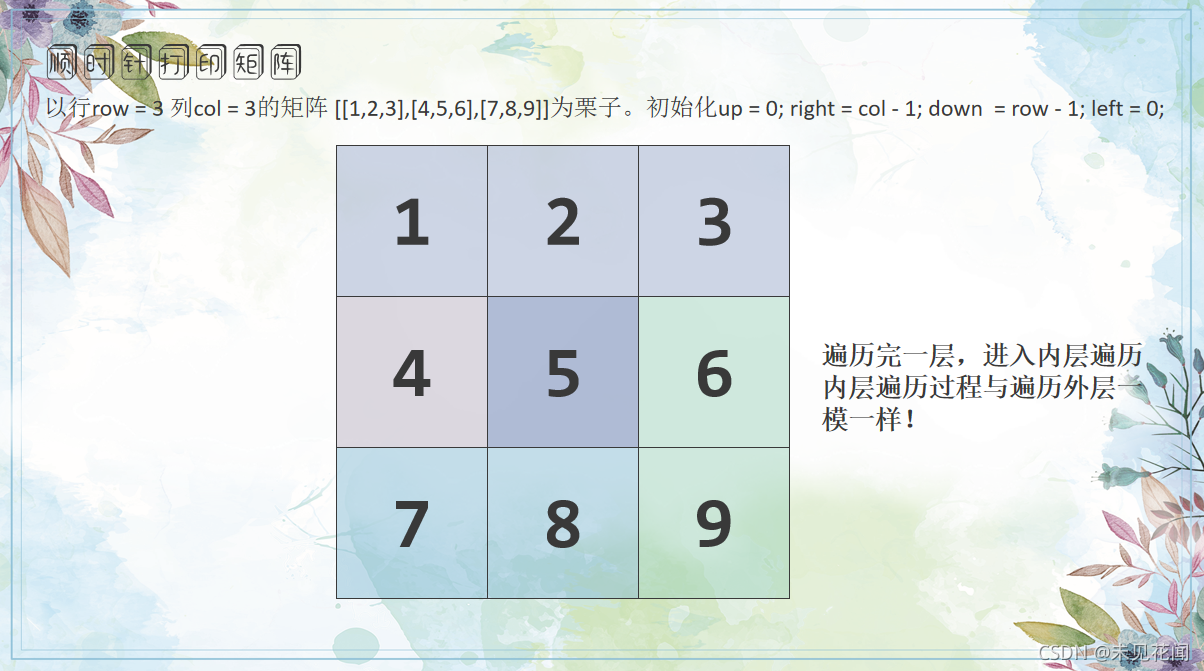
在生活中，我相信大家一定都接触过卷心菜或者洋葱，它们都是由许多层叠加包起来的。不知道你们剥过洋葱或卷心菜没有，对于这道题我们可以一层一层地剥开，先外后里，一层一层地遍历完所有的元素。
首先，我们需要对最外层进行遍历，然后再进一层，直到遍历完所有的元素。而每一层的遍历我们可以拆成4个部分，由于每次都是从左上角开始，所以遍历次序依次为顶行 右列 底行 左列，这四部分的指针分别为up right down left：

1. 顶行遍历完，up++
2. 右列遍历完，right--
3. 底行遍历完，down--
4. 左列遍历完，left++

每这样循环一轮，就相当于剥了一层洋葱，当底行指针小于顶行指针或左列指针大于右列指针就代表已经全部遍历完。或者在遍历过程中，并进行计数，当计数个数与总元素个数相同时代表元素遍历完成！
假设数组总元素个数为size。

时间复杂度： O(size)
空间复杂度： O(1)

🔑源代码

import java.util.*;

public class Printer {
    public int[] clockwisePrint(int[][] mat, int n, int m) {
        // write code here
        int[] ans = new int[n * m];
        //上
        int top = 0;
        //下
        int down = n - 1;
        //左
        int left = 0;
        //右
        int right = m - 1;
        
        //下标
        int idx = 0;
        while (idx < n * m) {
            //打印top行
            for (int j = left; j <= right; j++) {
                ans[idx++] = mat[top][j];
            }
            top++;
            if (top > down) break;
            //打印right列
            for (int i = top; i <= down; i++) {
                ans[idx++] = mat[i][right];
            }
            right--;
            if (left > right) break;
            //打印down行
            for (int j = right; j >= left; j--) {
                ans[idx++] = mat[down][j];
            }
            down--;
            if (top > down) break;
            //打印left列
            for (int i = down; i >= top; i--) {
                ans[idx++] = mat[i][left];
            }
            left++;
            if (left > right) break;
        }
        return ans;
    }
}

🌱总结

本题为简单模拟题。