N皇后问题分析与求解算法图解、流程图和复杂度
@TOC
一、问题描述
问题描述:n 皇后问题 研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。给你一个整数 n ,返回所有不同的 n 皇后问题 的解决方案。每一种解法包含一个不同的 n 皇后问题 的棋子放置方案,该方案中 ‘Q’ 和 ‘.’ 分别代表了皇后和空位。皇后彼此不能相互攻击,也就是说:任何两个皇后都不能处于同一条横行、纵行或斜线上。
以下是4皇后问题的结果模型:
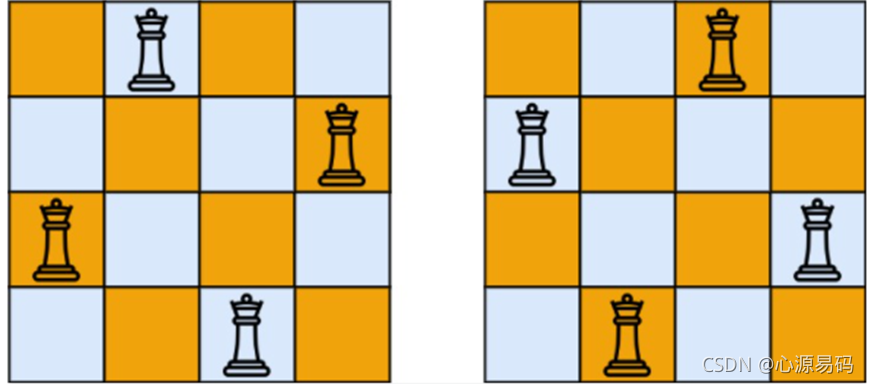
输入:n = 4
输出:[[".Q…","…Q",“Q…”,"…Q."],["…Q.",“Q…”,"…Q",".Q…"]]
解释:4皇后问题存在两个不同解法
输入:n = 1
输出:[[“Q”]]
解释:1皇后问题只存在一种解法
二、问题分析
该问题要求把n个皇后放在一个n×n的棋盘上,使任何两个皇后不能同行不能同列也不能位于同一对角线上。用回溯的思想对它求解:因为每个皇后都必须占据一行,所以我们的问题转化为给每行的皇后分配一个合适的列。
n=1,2,3时问题很简单,所以我们以n=4开始考虑,求解过程如下:
如下图是一个空的4皇后问题的棋盘模型,
我们从空棋盘开始,首先将皇后1放到它所在行的第一个可能位置(此时为第一列),即皇后1的坐标为(1,1);对于皇后2,尝试将其填入第一列检查是否符合规则,发现失败,第二列也失败,第三列符合要求,即将皇后2填入(2,3);再将皇后3依规则找第一个可能的位置,但是发现四个位置都不符合,所以将算法回溯,把皇后2放在下一个可能位置,即(2,4)上,这样皇后3可以放在(3,2),去找皇后4能不能放,此时又发现没有符合的位置,然后回溯到皇后3,皇后3没有再可以尝试的位置,回溯到皇后2也没有再可以尝试的位置,回溯到皇后1,把皇后1放在(1,2),接着按相同步骤将皇后2放在(2,4),皇后3放在(3,1),皇后4放在(4,3),这就是n=4时的一个解,接着再次回溯找剩下的解。
三、算法流程图
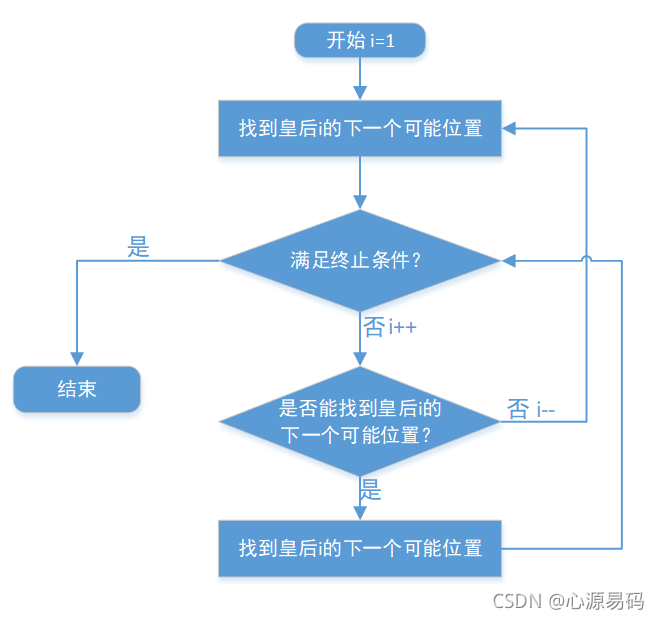
四、源码
class Solution {
List<List<String>> res = new ArrayList<>();
public List<List<String>> solveNQueens(int n) {
char[][] chessboard = new char[n][n];
for (char[] c : chessboard) {
Arrays.fill(c, '.');
}
backTrack(n, 0, chessboard);
return res;
}
public void backTrack(int n, int row, char[][] chessboard) {
if (row == n) {
res.add(Array2List(chessboard));
return;
}
for (int col = 0;col < n; ++col) {
if (isValid (row, col, n, chessboard)) {
chessboard[row][col] = 'Q';
backTrack(n, row+1, chessboard);
chessboard[row][col] = '.';
}
}
}
public List Array2List(char[][] chessboard) {
List<String> list = new ArrayList<>();
for (char[] c : chessboard) {
list.add(String.copyValueOf(c));
}
return list;
}
public boolean isValid(int row, int col, int n, char[][] chessboard) {
// 检查列
for (int i=0; i<row; ++i) { // 相当于剪枝
if (chessboard[i][col] == 'Q') {
return false;
}
}
// 检查45度对角线
for (int i=row-1, j=col-1; i>=0 && j>=0; i--, j--) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
// 检查135度对角线
for (int i=row-1, j=col+1; i>=0 && j<=n-1; i--, j++) {
if (chessboard[i][j] == 'Q') {
return false;
}
}
return true;
}
}
五、复杂度
时间复杂度为:O(N!)
分析:使用一个数组记录每行放置的皇后的列下标,依次在每一行放置一个皇后。每次新放置的皇后都不能和已经放置的皇后之间有攻击:即新放置的皇后不能和任何一个已经放置的皇后在同一列以及同一条斜线上,并更新数组中的当前行的皇后列下标。当 N个皇后都放置完毕,则找到一个可能的解。当找到一个可能的解之后,将数组转换成表示棋盘状态的列表,并将该棋盘状态的列表加入返回列表。
由于每个皇后必须位于不同列,因此已经放置的皇后所在的列不能放置别的皇后。第一个皇后有 N 列可以选择,第二个皇后最多有 N−1 列可以选择,第三个皇后最多有 N-2 列可以选择(如果考虑到不能在同一条斜线上,可能的选择数量更少),因此所有可能的情况不会超过 N!种,遍历这些情况的时间复杂度是 O(N!)。
- 点赞
- 收藏
- 关注作者


评论(0)