AcWing 蓝桥杯AB组辅导课 05、树状数组与线段树
【摘要】 前段时间为了在面试中能够应对一些算法题走上了刷题之路，大多数都是在力扣平台刷，目前是300+，再加上到了新学校之后，了解到学校也有组织蓝桥杯相关的程序竞赛，打算再次尝试一下，就想系统学习一下算法（再此之前是主后端工程为主，算法了解不多刷过一小段时间），前段时间也是第一次访问acwing这个平台，感觉上面课程也是比较系统，平台上题量也很多，就打算跟着acwing的课程来走一段路，大家一起共勉加油！所
@[toc]
前言
前段时间为了在面试中能够应对一些算法题走上了刷题之路，大多数都是在力扣平台刷，目前是300+，再加上到了新学校之后，了解到学校也有组织蓝桥杯相关的程序竞赛，打算再次尝试一下，就想系统学习一下算法（再此之前是主后端工程为主，算法了解不多刷过一小段时间），前段时间也是第一次访问acwing这个平台，感觉上面课程也是比较系统，平台上题量也很多，就打算跟着acwing的课程来走一段路，大家一起共勉加油！
- 目前是打算参加Java组，所以所有的题解都是Java。、
所有博客文件目录索引：博客目录索引(持续更新)
本章节树状数组、线段树及找规律的习题一览：包含所有题目的Java题解链接
例题：
- AcWing 1264. 树状数组-模板题 动态求连续区间和 Java题解、AcWing 1264. 线段树-模板题 动态求连续区间和 Java题解
- AcWing 1265. 树状数组-例题 数星星 Java题解
- AcWing 1270. 线段树-习题 数列区间最大值 Java题解
习题：
- AcWing 1215. 树状数组-习题 小朋友排队 Java题解（树状数组、归并排序两种解法，包含详细思路）
- AcWing 1228. 线段树-油漆面积 Java题解（详细图示+思路分析，困难，蓝桥杯）
- AcWing 1232. 差分—习题 三体攻击(三维差分，蓝桥杯) Java题解（详细分析及推导）
- AcWing 1237. 找规律—习题 螺旋折线 Java题解（含详细分析）
学习三体攻击题目的前置知识点-差分（一维、二维）：
一、树状数组
前缀和是离线做法，树状数组是在线做法。
1.1、树状数组知识点
学习：树状数组详解
树状数组或二叉索引树（Binary Indexed Tree），又以其发明者命名为 Fenwick 树。其初衷是解决数据压缩里的累积频率的计算问题，现多用于高效计算数列的前缀和、区间和。
复杂度：
- 时间复杂度：O(logn) 的时间得到任意前缀和，并同时支持在 O(logn) 时间内支持动态单点值的修改。
- 空间复杂度 O(n)。
重点就是利用二进制的变化，动态地更新树状数组。
支持的功能：单点查询、区间修改(前缀和)
- 其他问题可以通过转化来进行求解，如：
- ①进行区间修改、单点查询需要采用一个差分的思想并进行转化才可以。
- ②进行区间修改、区间查询也是差分。
与前缀和比较：
- 前缀和：查询O(1)；修改O(n)。总和时间为O(n)
- 树状数组：查询O(logn)；修改O(logn)。总和时间为logn
对于没有修改的时候使用前缀和是比较明智的选择，若是有大量的修改操作那么就不太建议使用前缀和了！
需要证明的点：
1、为什么之后一个结点包含它？
2、为什么这个证明就是加上lowbit?
具体介绍
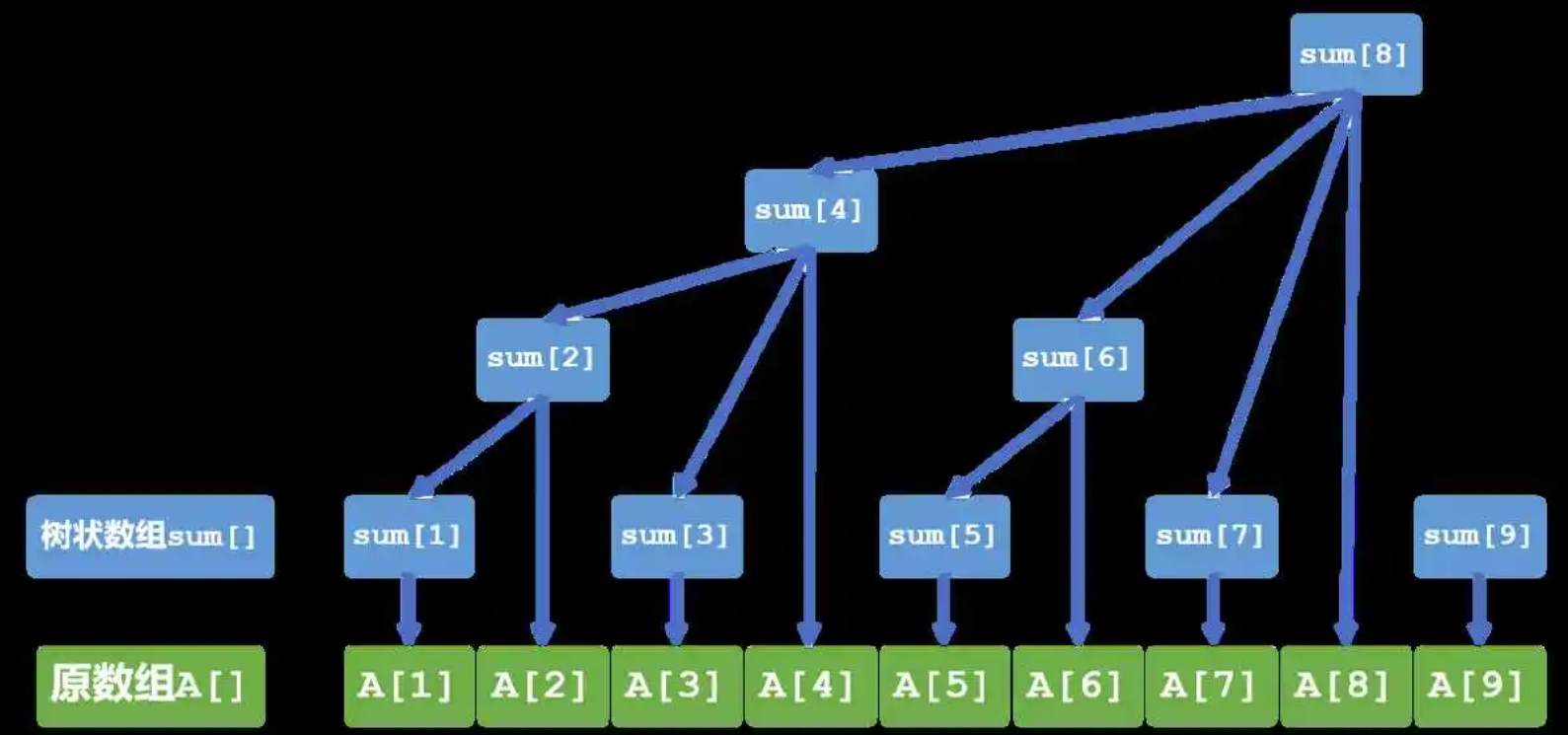
其中对于树状数组中某个下标位置表示的是一段范围的总值，例如：sum[1]表示[1,1]中的值，sum[3]表示[3,3]中的值，sum[6]表示[5,6]中的值，对于其中具体范围是根据一个lowbit()函数来进行计算的。
- lowbit(i) 表示 (i - lowbit(i), i]。一般的话lowbit(i) 实际上是使用 i & (i - 1)来计算得到这个值。
- lowbit()函数计算得到的实际上是对应二进制从右到左第一个1的位置(另其为k = index-1)，得到的值为2^k^。
- 如6，其二进制是110，第1个1从右到左是第2个，那么值为2^1^=2，前一个位置元素+当前位置元素就是两个，表示该C[6]=A[5]+A[6]
- 例如lowbit(1)得到值为1，lowbit(3)得到值为1，lowbit(6)得到值为2。
①计算C[i]的值，实际上就是在对应每个相应范围的父节点上进行加值
//其中4是目标位置，val表示该4位置需要相加的和
//更新一个值，需要更新后面的分段值
for (int i = 4; i <= 9; i += lowbit(i)){
C[i] += val;
}
//例如更新4位置，值为2
第一轮：i = 4, c[4] += 2，lowbit(4)=4
第二轮：i = 8, c[8] += 4，lowbit(8)=8
第三轮结束
②计算[0, i]范围前缀和
lowbit只是辅助得到index的合并范围，之后我们想要得到前缀和也是通过该函数来进行合并计算的。时间复杂度为O(logn)
举例：求6的前缀和
//计算和
for (int i = 6; i > 0; i -= lowbit(i)) {
ret += C[i];
}
第一轮：i = 6, lowbit(6) = 2 ret += C[6]
第二轮：i = 4, lowbit(4) = 4 ret += C[4]
第三轮结束
其中C[6] = sum[5] + sum[6]
C[4] = C[2] + sum[3] + sum[4]，又其中C[2]=sum[1] + sum[2]
1.2、树状数组代码模板
public class Main {
static final int N = 10010;
public static int[] C = new int[N];
//具体数组中的元素值
public static int n;
//根据当前的点确定该点的范围[i - lowbit(i), i]
static int lowbit(int i) {
return i & -i;//或者是return i-(i&(i-1));表示求数组下标二进制的非0最低位所表示的值
}
static void add(int x, int val)//单点更新
{
for (int i = x; i <= n; i += lowbit(i)) {
C[i] += val;//由叶子节点向上更新树状数组C，从左往右更新
}
}
static int sum(int x)//求区间[1,i]内所有元素的和
{
int ret = 0;
for (int i = x; i > 0; i -= lowbit(i)) {
ret += C[i];//从右往左累加求和
}
return ret;
}
public static void main(String[] args) {
n = 6;
//原始数组初始化
int[] arr = new int[7];
for (int i = 1; i <= n; i++) {
arr[i] = i;
}
//初始化树状数组
for (int i = 1; i <= n; i++) {
add(i, arr[i]);
}
//实践
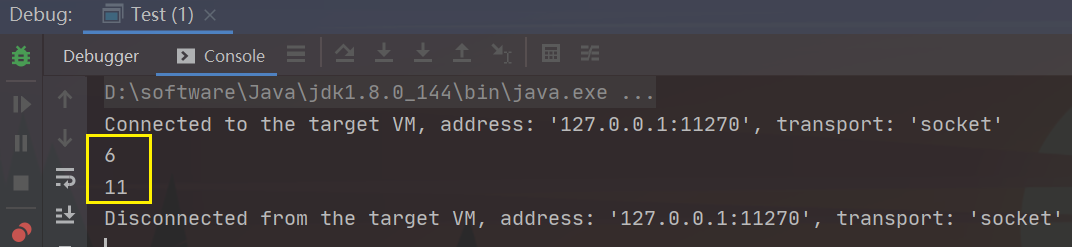
//1、查询前5个值，当前数组为{1, 2, 3, 4, 5, 6}
System.out.println(sum(3));//预计值为6
//2、给第二个位置上加上2。此时arr数组为{1, 4, 3, 4, 5, 6}
add(2, 2);
//3、计算[1, 4]范围的值。
System.out.println(sum(4) - sum(1));//预计值为11
}
}
模板题：AcWing 1264. 动态求连续区间和
题目链接：1264. 动态求连续区间和
分析：
本题实际上就是基本代码模板的一个示例题目，基本与代码模板一致，同样是针对于连续区间进行求和。
题解：
复杂度分析：时间复杂度O(nlogn)；空间复杂度O(n)
import java.util.*;
import java.io.*;
class Main {
static final BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
static final PrintWriter out = new PrintWriter(new BufferedOutputStream(System.out));
static final int N = 100010;
static int n, m;
//arr：原数组、tr：树状数组
static int[] arr = new int[N], tr = new int[N];
public static int lowbit(int x) {
return x & -x;
}
//add i val：添加到指定位置值
public static void add(int x, int val) {
for (int i = x; i <= n; i += lowbit(i)) {
tr[i] += val;
}
}
//sum i：求[1,i]的所有和
public static int sum(int x) {
int ret = 0;
for (int i = x; i > 0; i -= lowbit(i)) {
ret += tr[i];
}
return ret;
}
public static void main(String[] args) throws Exception {
String[] s = cin.readLine().split(" ");
n = Integer.valueOf(s[0]);
m = Integer.valueOf(s[1]);
s = cin.readLine().split(" ");
//初始化
for (int i = 1; i <= n; i++) {
arr[i] = Integer.valueOf(s[i - 1]);
//添加到树状数组
add(i, arr[i]);
}
//读取m行数据来进行响应技术
while (m-- != 0) {
s = cin.readLine().split(" ");
int k = Integer.valueOf(s[0]);
int a = Integer.valueOf(s[1]);
int b = Integer.valueOf(s[2]);
if (k == 0) {
//求[a,b]的和
out.println(sum(b) - sum(a - 1));
}else {
//第 a 个数加 b
add(a, b);
}
}
out.flush();
}
}
例题
例题1、AcWing 1265. 数星星【中等，信息学奥赛一本通】
题目链接：1265. 数星星
分析：
看上去是一个二维的平面图。
细节：由于是给出的坐标点都是从左往右，接着从下往上的，所以实际上我们无需去区分x，y点，只需要计算在x位置的数量即可，因为顺序是先从下往上，那么对于同x位置的，在上面的统计时也会把下方同位置的一起统计。
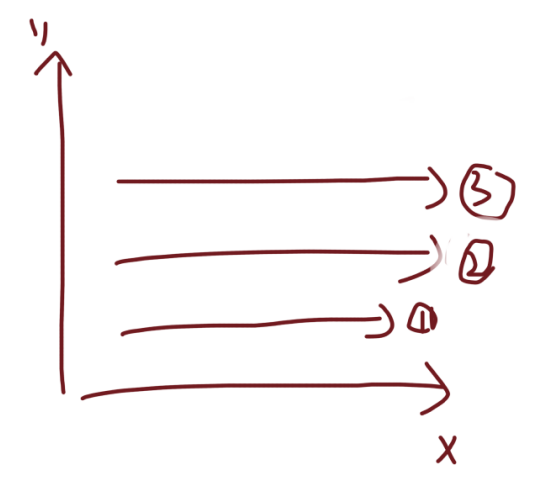
核心：每颗星星只需要对其x来进行加1即可，计算sum实际上就是统计[1, x]位置的即可。
本道题用Java解的一些问题：
1、因为限时时间太短，所以输入、输出函数需要使用BufferedReader和PrintWriter，不然就会报超时。
题解：
复杂度分析：时间复杂度O(logn)；空间复杂度O(n)
import java.util.*;
import java.io.*;
class Main {
static BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
static PrintWriter out = new PrintWriter(new BufferedOutputStream(System.out));
static final int N = 32010;
static int n;
//树状数组、索引数组
static int[] tr = new int[N], index = new int[N];
public static int lowbit(int x) {
return x & -x;
}
//在x位置+1
public static void add(int x) {
for (int i = x; i < N; i += lowbit(i)) {
tr[i]++;
}
}
//计算前缀和
public static int sum(int x) {
int ret = 0;
for (int i = x; i > 0; i -= lowbit(i)) {
ret += tr[i];
}
return ret;
}
public static void main (String[] args) throws Exception{
n = Integer.parseInt(cin.readLine());
for (int i = 0; i < n; i++) {
String[] s = cin.readLine().split(" ");
int x = Integer.parseInt(s[0]);
x++;
//统计星级的数量（统计出为0的数量）
index[sum(x)]++;
//再进行加1
add(x);
}
for (int i = 0; i < n; i++) {
//效率由高到低比较：
//[PrintWriter].println() > [PrintWriter].printf() > System.out.println() > System.out.printf()
//经过测试：out.println(index[i]); 比 out.printf("%d\n", index[i])效率更高，后者在该题中也会超时。
out.println(index[i]);
}
out.flush();
}
}
习题
习题1：1215. 小朋友排队【中等，蓝桥杯】
题目链接：1215. 小朋友排队
分析：
首先看一下数据范围，10万数据量，那么就是O(n.logn)、O(n)的时间复杂度
树状数组思路：
如何求得每个小朋友的交换次数？
- 每个小朋友之前小朋友>该小朋友的身高的数量 + 每个小朋友之后小朋友<该小朋友的身高的数量。
问题：那么我们如何高效的得到每个小朋友之前与之后的数量呢？
答：暴力的话复杂度为O(n^2^)；使用树状数组的话就是O(nlogn)就能够计算出来了。对于之前数量通过从前往右遍历一遍+添加到树状数组中可获取，之后数量则是从后往前遍历一遍+添加到树状数组。
得到了交换的次数那么怎么与生气值关联起来，举例：
- 交换1次：1 = 1
- 交换2次：1+2 = 3
- 交换3次：1+2+3 = 6
得到式子：生气值 = （交换次数 x (交换次数 + 1)）/ 2
归并排序思路：
本质上与树状数组思路大体一致，同样是求到每个小朋友需要移动的次数，接着来计算生气值。只不过在这里并没有通过树状数组来求得小于或大于某个小朋友的数量，而是通过归并排序来进行求得某个小朋友需要交换的次数。
举例子：
[5, 7, 4, 6]
归并排序的过程如下：
[5, 7] [4, 6]
[5] [7] [4] [6]
=== 开始回溯 ===
[5, 7] [4, 6]
[4, 5, 6, 7]
关键来看[5, 7] [4, 6] => [4, 5, 6, 7]这个过程中的每个节点需要交换的次数
i表示从[5,7]的第一个位置开始，j表示从[4,6]的第一个位置开始 => i = 0, j = 2 mid = 1
第一次比较：5 > 4 temp=[4]，此时就需要将左边框中的4移动到第一个位置，很显然需要移动两次，怎么计算呢？mid - i + 1即可求得2，也就是4要移动2次，那么此时cnt[4] += 2。此时j++，j = 3
第二次比较：5 < 6 temp=[4,5]，此时就需要将右边框子中的5移动到第二个位置，很显然需要移动一次，怎么计算？主要关键在于要看右边框中数移走了几位，那么同样可通过 j - (mid + 1)求得1，表示5要移动一次，那么此时cnt[5] += 1。此时i++，i = 1
第三次比较：7 > 6 temp[4, 5, 6] 同理 mid - i + 1 = 1，cnt[6] += 1，j++
最后跳转循环（由于i<=mid && j <= r），处理各自剩余框中元素，此时由两种情况，左框有剩余或者右框有剩余
对于左框有剩余，需要计算移动次数j - (mid + 1)得2，cnt[7] += 2
对于右框有剩余，由于temp数组长度与源数组一致，那么对于最右边框中的剩余元素根本就无需进行移动。
最后梳理下：
cnt[4] = 2
cnt[5] = 1
cnt[6] = 1
cnt[7] = 2
生气值为 = 2 * 3 / 2 + 1 * 2 / 2 + 1 * 2 / 2 + 2 * 3 / 2 = 3 + 1 + 1 + 3 = 8
此时就可以得到生气值为8啦
做法1：树状数组
复杂度分析：时间复杂度O(nlogn)；空间复杂度O(n)
//交换规则：每次只能交换位置相邻；每个小朋友交换的不高兴程度是之前的+1
//最终目标：身高从低到高，计算最小的不高兴程度之和
import java.util.*;
import java.io.*;
class Main {
static final BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
static final PrintWriter out = new PrintWriter(new BufferedOutputStream(System.out));
static final int N = (int)(1e6 + 10);
//定义身高数组、树状数组
static int[] h = new int[N], tr = new int[N];
//统计每个小朋友之前(大于他身高的)+之后(小于他身高的)数量
static int[] sum = new int[N];
public static int lowbit(int x) {
return x & -x;
}
public static void add(int x, int v) {
for (int i = x; i < N; i += lowbit(i)) {
tr[i] += v;
}
}
public static int query(int x) {
int res = 0;
for (int i = x; i > 0; i -= lowbit(i)) {
res += tr[i];
}
return res;
}
public static void main(String[] args)throws Exception {
int n = Integer.parseInt(cin.readLine());
String[] s = cin.readLine().split(" ");
for (int i = 0; i < n; i++) {
h[i] = Integer.parseInt(s[i]);
h[i]++;//规避身高为0的情况，若是身高为0，若是直接找之前的就是-1，-1不太好作为下标进行索引
}
//从前往后遍历一遍小朋友身高（确定每个小朋友之前且身高大于该小朋友的数量）
for (int i = 0; i < n; i++) {
//身高范围在[h[i] + 1, N - 1]的小朋友数量
sum[i] = query(N - 1) - query(h[i]);
//添加到前缀数组中（此时添加）
add(h[i], 1);
}
//初始化树状数组
Arrays.fill(tr, 0);
//从后往前遍历一遍小朋友身高（（确定每个小朋友之后且身高小于该小朋友的数量）
for (int i = n - 1; i >= 0; i--) {
//身高范围在[0, h[i] - 1]的小朋友数量（注意之前进行了h[i]++，所以只需要h[i]即可）
sum[i] += query(h[i] - 1);
//重复添加一遍
add(h[i], 1);
}
//最后遍历一遍sum（每个小朋友的左右数量来累加并得到不高兴程度和）
long res = 0;
for (int i = 0; i < n; i++) {
int count = sum[i];
//需要转为long类型
res += (long)count * (count + 1) >> 1;
}
System.out.println(res);
}
}
做法2：归并排序
复杂度分析：时间复杂度：O(nlogn)；空间复杂度O(n)
import java.util.*;
import java.io.*;
class Node {
public int h;//身高
public int index;//初始Node节点的编号（用于定位cnt数组中的索引）
public Node(int h, int index) {
this.h = h;
this.index = index;
}
}
class Main {
static final BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
static final PrintWriter out = new PrintWriter(new BufferedOutputStream(System.out));
static final int N = (int)(1e6 + 10);
//身高数组
static Node[] childs = new Node[N];
//定位节点
static int[] cnt = new int[N];
//归并排序
public static void mergeSort(int l, int r) {
if (l >= r) return;
int mid = (l + r) >> 1;
mergeSort(l, mid);
mergeSort(mid + 1, r);
//开始进行排序
Node[] temp = new Node[r - l + 1];
int i = l, j = mid + 1;
int k = 0;
while (i <= mid && j <= r) {
//例子：[5, 7] [4, 6] temp=[], mid = 1
//5 > 4 temp=[4] cnt[4] += 1 - 0 + 1 = 2
//5 < 6 temp=[4, 5] 注意了这个5相对于原始位置上也移动了一次，这个1次怎么计算？j - (mid + 1)
//7 > 6 temp=[4, 5, 6] 此时也只移动1次，mid - i + 1 = 1
if (childs[i].h <= childs[j].h) {
cnt[childs[i].index] += j - (mid + 1);
temp[k++] = childs[i++];
}else {
//左边的>右边的（无需进行交换）
cnt[childs[j].index] += mid - i + 1;
temp[k++] = childs[j++];
}
}
//处理左边剩余的
while (i <= mid) {
cnt[childs[i].index] += j - (mid + 1);
temp[k++] = childs[i++];
}
//处理右边剩余的
while (j <= r) {
temp[k++] = childs[j++];
}
//进行拷贝
for (i = l, j = 0; i <= r; i++, j++) {
childs[i] = temp[i - l];
}
}
//归并排序解法
public static void main(String[] args)throws Exception {
int n = Integer.parseInt(cin.readLine());
String[] s = cin.readLine().split(" ");
for (int i = 0; i < n; i++) {
childs[i] = new Node(Integer.parseInt(s[i]), i);
}
mergeSort(0, n - 1);
//遍历所有孩子的编号并来进行计算
long res = 0;
for (int i = 0; i < n; i++) {
int count = cnt[i];
res += (long)count * (count + 1) >> 1;
}
System.out.println(res);
}
}
二、 线段树
知识点
线段树是一棵二叉树，而树状数组是一个多叉树。
操作1：单点修改。【涉及到递归回溯，修改最底下位置的值，最后来回溯计算当前结点值(左节点+右节点)】
操作2：区间查询。
- 最大查询时间为O(4logn)，实际上就是O(logn)
是否支持区间修改，区间查询？
- 肯定是可以的，大部分的区间查询都是涉及到比较麻烦的问题，需要加一个额外的标记【懒标记】。
- 加懒标记的难度会涨很大。4 -> 8，一般在蓝桥杯中是用不上的。
大部分情况下就是做单点修改与区间查询。
y总思路梳理总结：
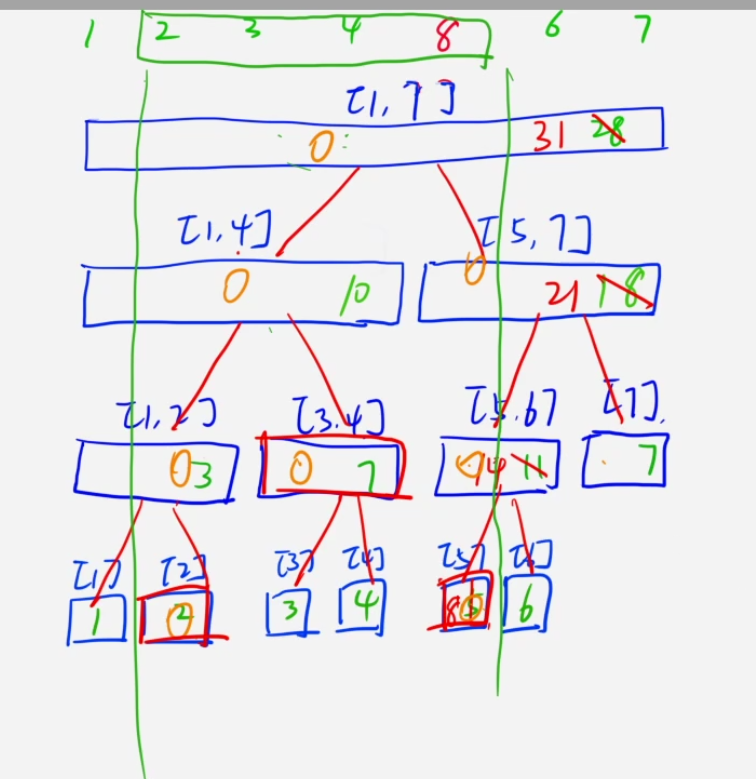
- 单点修改：指定左或者右(一条路径)来进行递归下去，实际修改掉值之后，就会进行回溯向上计算最新的区间范围值。【右边红线杉删除的情况，单点修改5位置的值为8】
- 区间查询：左右子树只要在范围内就都会进行向下递归，直到找到最合适的范围来进行向上递归返回。【查询[2,5]的范围，即可找到位置[2]、[3,4]、[5]】
模板题：AcWing 1264. 动态求连续区间和
题目链接：1264. 动态求连续区间和
分析：
简单调用一波模板函数即可。
题解：
复杂度分析：时间复杂度O(logn)；空间复杂度O(n)
import java.util.*;
import java.io.*;
class Main {
static final int N = 100010;
static BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
static PrintWriter out = new PrintWriter(new BufferedOutputStream(System.out));
static int n, m;
//接收输入的权重值
static int[] w = new int[N];
//线段树：需要开4倍空间
static Node[] tr = new Node[N * 4];
//树状数组节点
static class Node {
public int l, r;
public int sum;
public Node(int l, int r, int sum) {
this.l = l;
this.r = r;
this.sum = sum;
}
public Node(int l, int r) {
this.l = l;
this.r = r;
}
}
//计算当前节点信息的两个儿子节点之和
public static void push_up(int u) {
tr[u].sum = tr[u << 1].sum + tr[u << 1 | 1].sum;
}
//构建线段树
//u：当前节点编号；l：左边界；r：右边界
public static void build(int u, int l, int r) {
if (l == r) tr[u] = new Node(l, r, w[r]);
else {
tr[u] = new Node(l, r);//赋值左右边界的初值，当前并不计算sum值
int mid = (l + r) >> 1;
//递归左、右儿子
build(u << 1, l, mid);
build(u << 1 | 1, mid + 1, r);
//更新当前节点信息
push_up(u);
}
}
//查询：从根结点开始往下找对应的一个区间。该结点是左右两边根据具体的范围来进行向下递归，左右通吃
//u：当前结点编号。l：确定左边范围。r：确定右边范围。
public static int query(int u, int l, int r) {
//若是当前区间完全包含了，直接返回它的值就好
if (l <= tr[u].l && tr[u].r <= r) return tr[u].sum;
//记录中点
int mid = (tr[u].l + tr[u].r) >> 1;
int sum = 0;
//看当前区间的中点与左边有没有交集（符合条件就进行向左下、右下递归）
if (mid >= l) sum += query(u << 1, l, r);
if (r >= mid + 1) sum += query(u << 1 | 1, l, r);
return sum;
}
//修改函数。【左右确定单个路径向下，最后向上回溯计算节点值】
//u：当前节点的编号。x：要修改的位置。v：增加的值
public static void modify (int u, int x, int v) {
//若是当前到达叶子节点，计算sum值
if (tr[u].l == tr[u].r) {
tr[u].sum += v;
}else {
//计算当前节点元素的中间值
int mid = (tr[u].l + tr[u].r) >> 1;
//确定要找的x是在左边还是右边
if (x <= mid) {
modify(u << 1, x, v);//向左递归
}else {
modify(u << 1 | 1, x, v);//向右递归
}
//递归回溯时重新计算当前的节点值
push_up(u);
}
}
public static void main(String[] args) throws Exception {
String[] s = cin.readLine().split(" ");
n = Integer.parseInt(s[0]);
m = Integer.parseInt(s[1]);
s = cin.readLine().split(" ");
for (int i = 1; i <= n; i++) {
w[i] = Integer.parseInt(s[i - 1]);
}
//初始化
build(1, 1, n);
while (m-- != 0) {
s = cin.readLine().split(" ");
int k = Integer.parseInt(s[0]);
int a = Integer.parseInt(s[1]);
int b = Integer.parseInt(s[2]);
if (k == 0) {
//查询[a,b]范围的值
out.println(query(1, a, b));
}else {
//修改指定a位置的值为b
modify(1, a, b);
}
}
out.flush();
}
}
例题
例题1：1270. 数列区间最大值【简单】
题目链接：1270. 数列区间最大值
分析：
实际上就是将求线段树模板题中区间和替换为求最大值。
题解：
复杂度分析：时间复杂度O(logn)；空间复杂度O(n)
import java.util.*;
import java.io.*;
class Main {
static final BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
static final PrintWriter out = new PrintWriter(new BufferedOutputStream(System.out));
static final int N = 100010;
static int n, m;
static int[] w = new int[N];
static Node[] tr = new Node[N * 4];
static class Node {
public int l, r;
public int max;
public Node(int l, int r, int max) {
this.l = l;
this.r = r;
this.max = max;
}
public Node(int l, int r) {
this.l = l;
this.r = r;
}
}
//更新最新值（取最大值）
public static void push_up(int u) {
tr[u].max = Math.max(tr[u << 1].max, tr[u << 1 | 1].max);
}
//构建
public static void build(int u, int l, int r) {
if (l == r) tr[u] = new Node(l, r, w[l]);
else {
//初始化左右节点
tr[u] = new Node(l, r);
//计算左右两个值
int mid = l + r >> 1;
build(u << 1, l, mid);
build(u << 1 | 1, mid + 1, r);
//更新最新值
push_up(u);
}
}
//查询
public static int query(int u, int l, int r) {
//在确定范围当中直接返回
if (l <= tr[u].l && tr[u].r <= r) return tr[u].max;
int mid = tr[u].l + tr[u].r >> 1;
//这里就不是求和，而是来进行求最大值
int max = Integer.MIN_VALUE;
if (mid >= l) max = Math.max(max, query(u << 1, l, r));
if (r >= mid + 1) max = Math.max(max, query(u << 1 | 1, l, r));
return max;
}
//区间范围最大值
public static void main (String[] args) throws Exception {
String[] s = cin.readLine().split(" ");
n = Integer.parseInt(s[0]);
m = Integer.parseInt(s[1]);
s = cin.readLine().split(" ");
for (int i = 1; i <= n; i++) {
w[i] = Integer.parseInt(s[i - 1]);
}
build(1, 1, n);
while (m-- != 0) {
s = cin.readLine().split(" ");
int x = Integer.parseInt(s[0]);
int y = Integer.parseInt(s[1]);
out.println(query(1, x, y));
}
out.flush();
}
}
习题
习题1：1228. 油漆面积【困难，蓝桥杯】
题目链接：1228. 油漆面积：
分析：
题意就是给我们多个矩形，这些矩形的区域可能会重叠，我们需要计算出所有矩形的面积之和（重叠的面积只需要算一份即可）。
根据题目给出的数据范围，n的长度为1万，时间复杂度应当为O(nlogn)。
直接来拿输入案例举例：
3
1 5 10 10
3 1 20 20
2 7 15 17
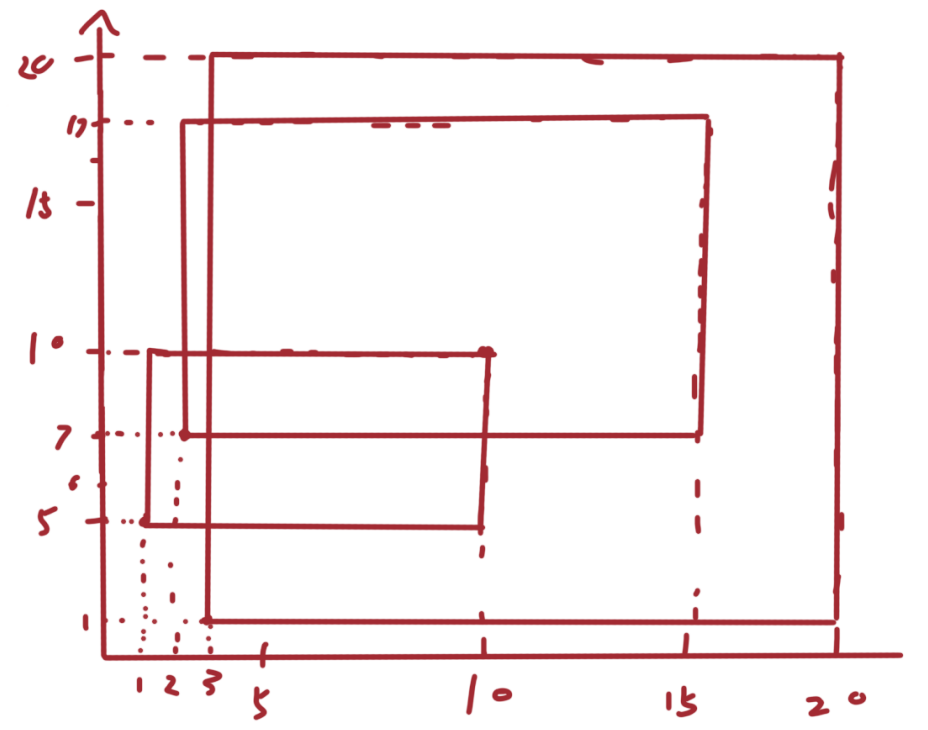
那么对于所有矩形如何进行计算总面积呢？可以采用一种【扫描线的思路】，从左至右来开始进行扫描：
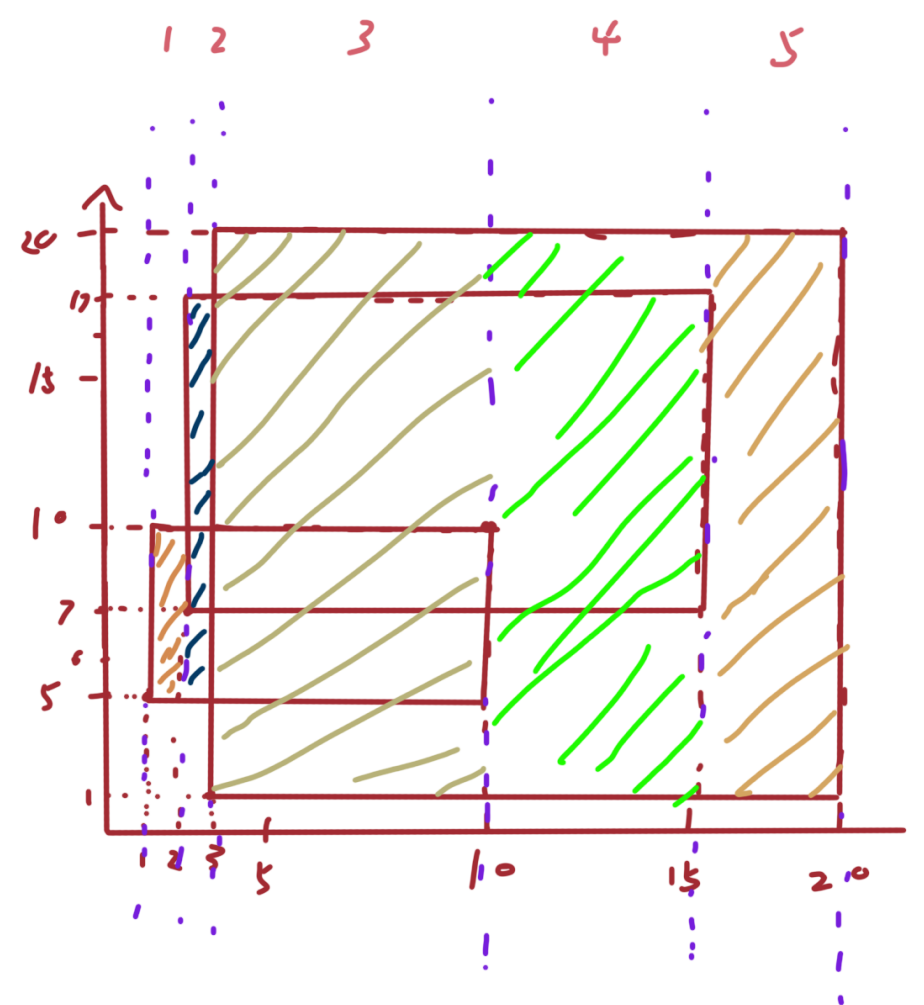
可以看到上图中根据标号，我们总共计算了5个矩形面积并进行相加即可求得总面积。
单个矩形的面积公式为 = 两条边的x坐标值相减绝对值 * 对应x范围内的y轴的总长度。
其中对于y轴总长度是比较难求得的，因为可能会有不同的矩形在同一个x上，以及矩形可能不是连续的如下：
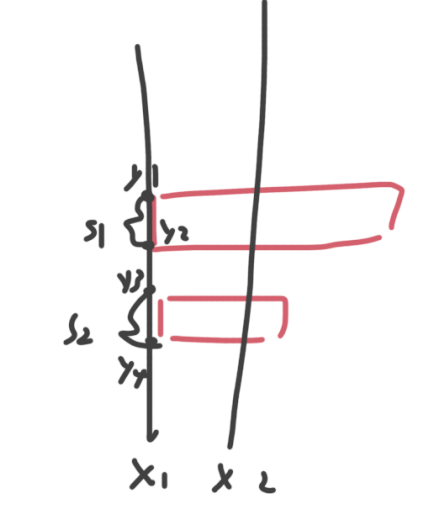
- 面积为 = (x2 - x1) * (s1 + s2)，其中s1=y1-y2，s2=y3-y4。
- 那么对于高度，实际上就是我们之前所说的x1-x2之间的高度长度范围，我们用一个len来表示，对于该图就是len=(y1-y2) + (y3-y4)=s1+s2，得到len后，即面积=(x2 - x1) * len
那么对于这个len的值总长度就是一个十分大的难点了，梳理下就是在区间范围中矩形的总长度，此时我们就可以采用线段树来进行解决该问题！
针对于上面输入案例来进行梳理下流程：
在线段树中其中pushup()更新结点的操作是根据cnt来确定len的取值：
cnt > 0 => len = r - l + 1
cnt = 0 && l == r => len = 0
cnt = 0 && l != r => len = 左儿子.len + 右儿子.len
下面是每次遍历边时的更新过程：
①update(1, 5, 9, 1)
②update(1, 7, 16, 1)
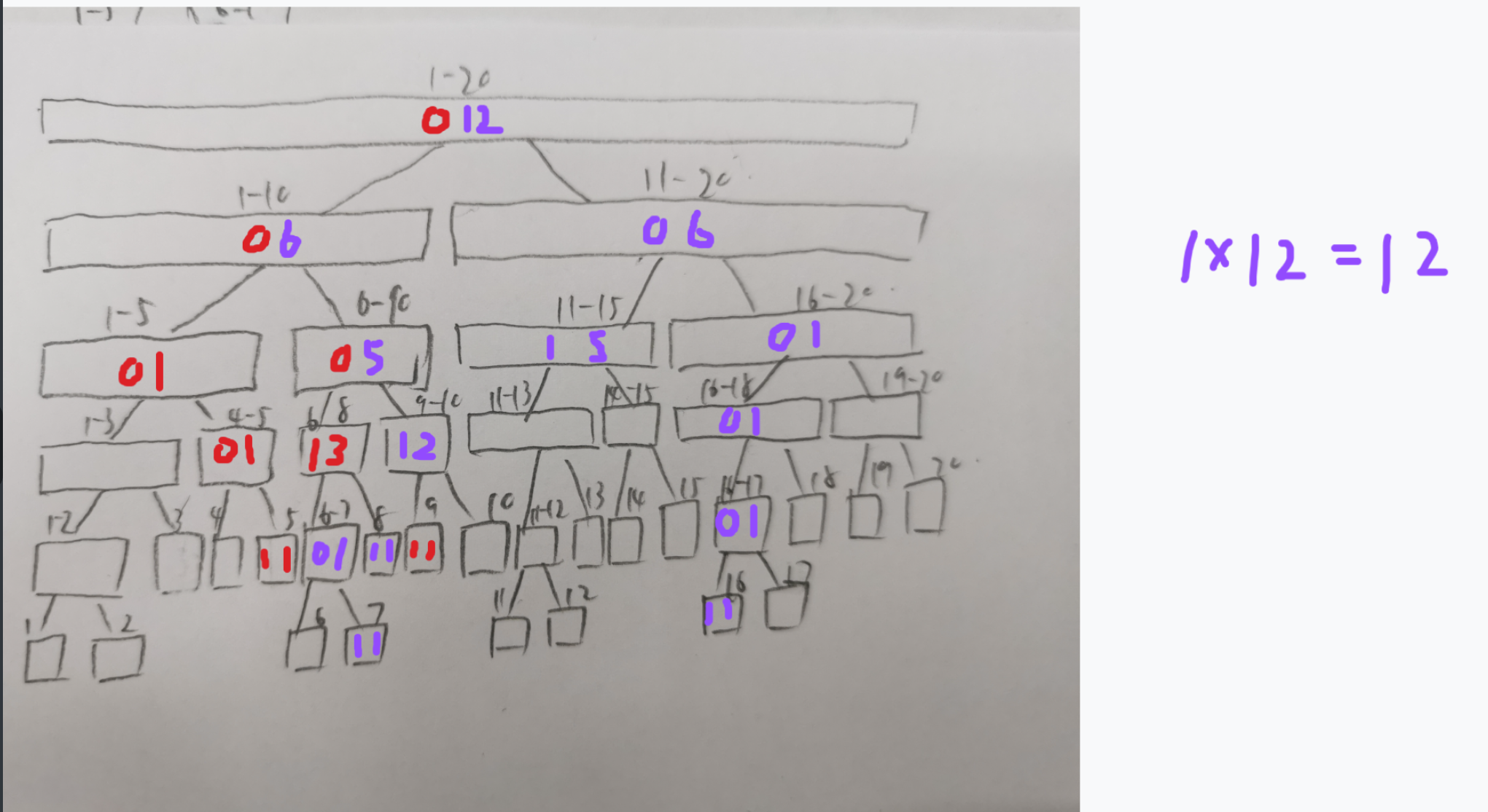
③update(1, 1, 19, -1)
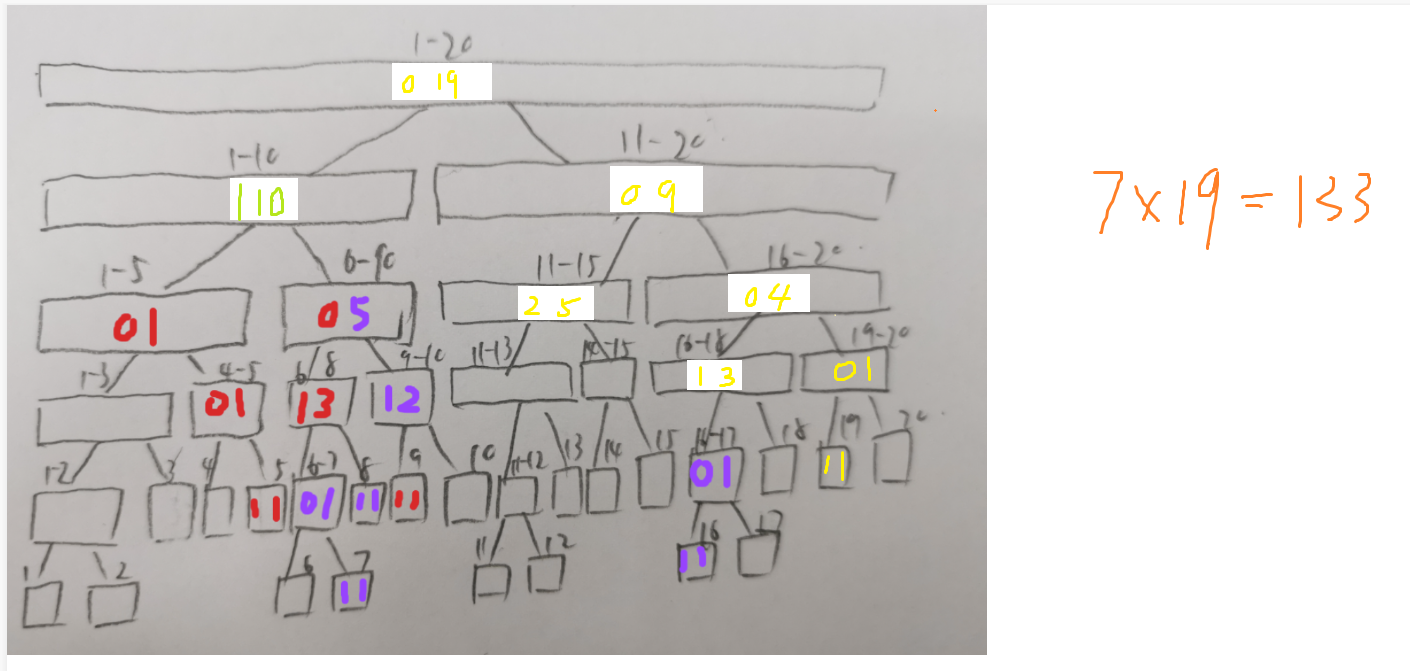
④update(1, 5, 9, -1)
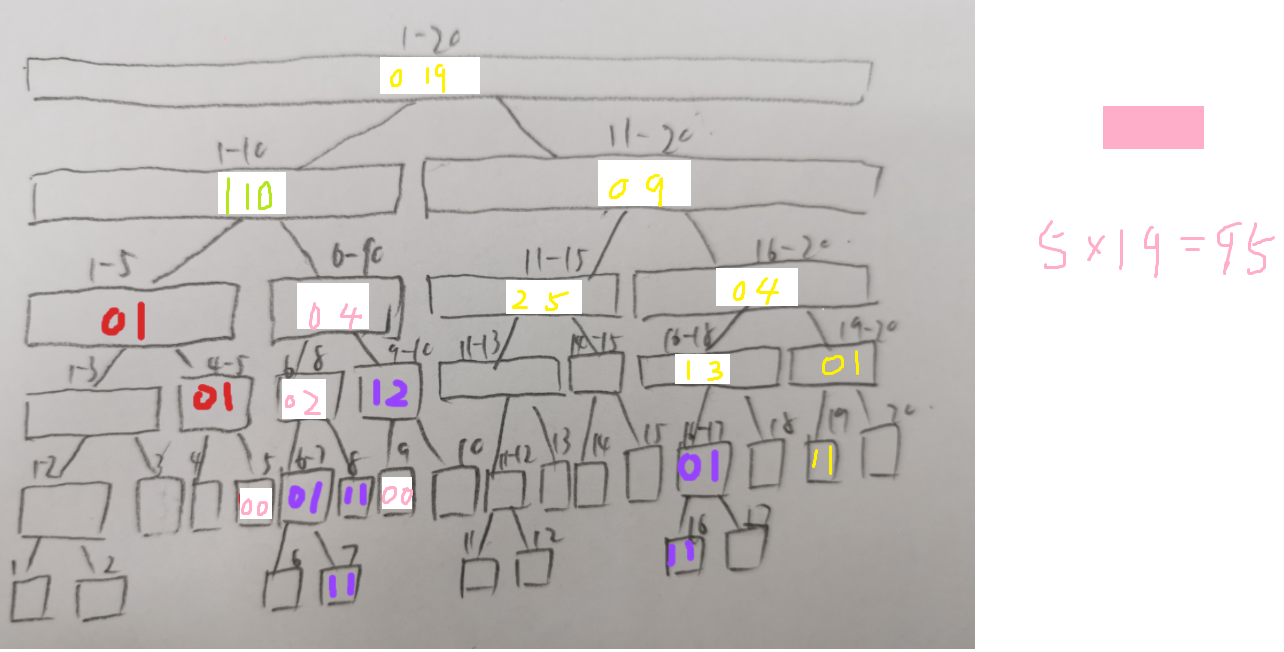
⑤update(1, 7, 16, -1)
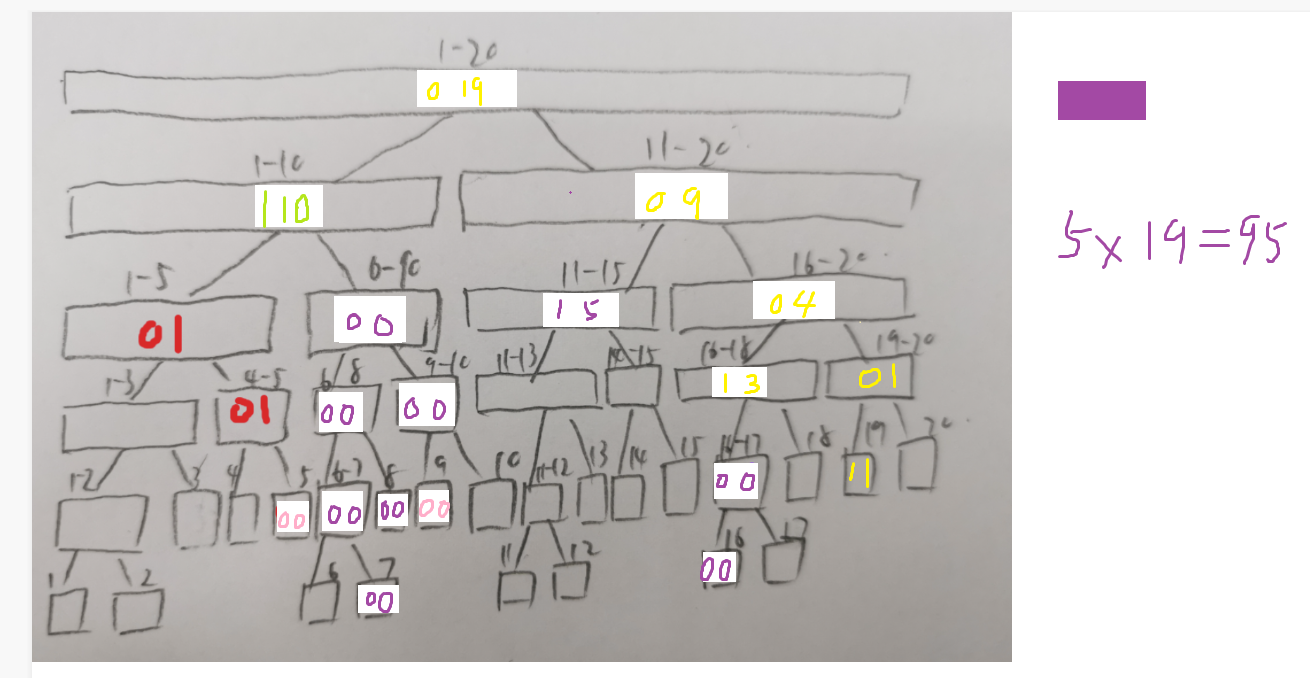
最后我们来计算下面积：s = 5 + 12 + 133 + 95 + 95 = 340
思路1：扫描线+线段树
复杂度分析：时间复杂度O(nlogn)；空间复杂度O(n)
import java.util.*;
import java.io.*;
//扫描线+线段树
//边
class Segment implements Comparable<Segment>{
int x1;
int y1;
int y2;
int cnt;//1表示是入边；0表示是出边
public Segment(int x1, int y1, int y2, int cnt) {
this.x1 = x1;
this.y1 = y1;
this.y2 = y2;
this.cnt = cnt;
}
@Override
public int compareTo(Segment s) {
return this.x1 - s.x1;
}
}
//线段树结点
class Node {
//左右范围
int l, r;
//覆盖的次数
int cnt;
//当前范围包含的长度（由cnt决定，cnt>0表示覆盖，此时就需要计算[l, r]的长度；若是cnt == 0 && l == r，此时len=0；若是cnt == 0 && l != r，len=left.len + right.len）
int len;
public Node(int l, int r) {
this.l = l;
this.r = r;
}
}
class Main {
static final BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
static final int N = 10010;
//线段树结点设置4倍的N
static Node[] tr = new Node[4 * N];
//边的长度
static Segment[] segments = new Segment[2 * N];
//构建树
public static void build (int u, int l, int r) {
if (l == r){
tr[u] = new Node(l, r);
}else {
tr[u] = new Node(l, r);
int mid = (l + r) >> 1;
//递归左、右儿子
build(u << 1, l, mid);
build(u << 1 | 1, mid + 1, r);
}
}
//更新当前的节点值
public static void pushUp(int u) {
//若是当前节点的cnt>0表示被覆盖，此时直接计算覆盖的区间范围长度
if (tr[u].cnt > 0) {
tr[u].len = tr[u].r - tr[u].l + 1;
}else if (tr[u].l == tr[u].r) {
//cnt == 0 && l == r，此时长度即为0
tr[u].len = 0;
}else {
tr[u].len = tr[u << 1].len + tr[u << 1 | 1].len;
}
}
//修改值
public static void modify(int u, int l, int r, int cnt) {
//若是当前的节点包含再次范围当中，对线段树结点中的cnt覆盖值进行更新
if (tr[u].l >= l && tr[u].r <= r) {
tr[u].cnt += cnt;
}else {
//拆分左右区间范围，递归向下去查找
int mid = (tr[u].l + tr[u].r) >> 1;
if (l <= mid) modify(u << 1, l, r, cnt);
if (r > mid) modify(u << 1 | 1, l, r, cnt);
}
//根据cnt覆盖的次数更新下当前范围的len
pushUp(u);
}
public static void main (String[] args)throws Exception {
int n = Integer.parseInt(cin.readLine());
int k = 0;
for (int i = 0; i < n; i++) {
String[] s = cin.readLine().split(" ");
int x1 = Integer.parseInt(s[0]);
int y1 = Integer.parseInt(s[1]);
int x2 = Integer.parseInt(s[2]);
int y2 = Integer.parseInt(s[3]);
//每一个正方形都包含一个入边与出边
segments[k++] = new Segment(x1, y1, y2, 1);
segments[k++] = new Segment(x2, y1, y2, -1);
}
//排序所有边（根据入边来进行排序）
Arrays.sort(segments, 0, 2 * n);
//从节点1开始，范围为[0, 10000]
build(1, 0, 10000);
//遍历所有的边（2 * n个）
int res = 0;
for (int i = 0; i < 2 * n; i++) {
//第二条边开始来进行计算面积
if (i > 0) {
//宽：segments[i].x1 - segments[i - 1].x1 长：tr[1].len
res += (segments[i].x1 - segments[i - 1].x1) * tr[1].len;
}
//更新当前边的信息
modify(1, segments[i].y1, segments[i].y2 - 1, segments[i].cnt);
}
System.out.println(res);
}
}
参考文章
[1]. ACWing 797. 差分（C++）、bilibili—一维差分(算法)
[2]. AcWing 1237. 螺旋折线
【版权声明】本文为华为云社区用户原创内容，转载时必须标注文章的来源（华为云社区）、文章链接、文章作者等基本信息， 否则作者和本社区有权追究责任。如果您发现本社区中有涉嫌抄袭的内容，欢迎发送邮件进行举报，并提供相关证据，一经查实，本社区将立刻删除涉嫌侵权内容，举报邮箱：
cloudbbs@huaweicloud.com
- 点赞
- 收藏
- 关注作者
评论（0）