@[toc]

前言

前段时间为了在面试中能够应对一些算法题走上了刷题之路，大多数都是在力扣平台刷，目前是300+，再加上到了新学校之后，了解到学校也有组织蓝桥杯相关的程序竞赛，打算再次尝试一下，就想系统学习一下算法（再此之前是主后端工程为主，算法了解不多刷过一小段时间），前段时间也是第一次访问acwing这个平台，感觉上面课程也是比较系统，平台上题量也很多，就打算跟着acwing的课程来走一段路，大家一起共勉加油！

• 目前是打算参加Java组，所以所有的题解都是Java。

本章节二分与前缀和的习题一览：包含所有题目的Java题解链接

例题：无链接的直接见当前博客

• 数的范围：模板题
• 数的三次方根：模板题
• AcWing 795. 前缀和-模板题(一维) 前缀和 Java题解
• AcWing 796. 前缀和-模板题(二维) 子矩阵的和 Java题解

习题：

• AcWing 730. 机器人跳跃问题 Java题解
• AcWing 1221. 四平方和 Java题解
• AcWing 1227. 分巧克力 二分 Java题解
• AcWing 99. 前缀和(二维) 激光炸弹 Java题解
• AcWing 1230. 前缀和(二维) K倍区间 Java题解 精简分析

一、二分

整数二分

知识点

1、确定一个区间，目标值一定在这个区间中。

2、找一个性质，使得这个性质满足两点：①具有二段性【前半段满足，后半段不满足】。②答案是二段性的分界点。

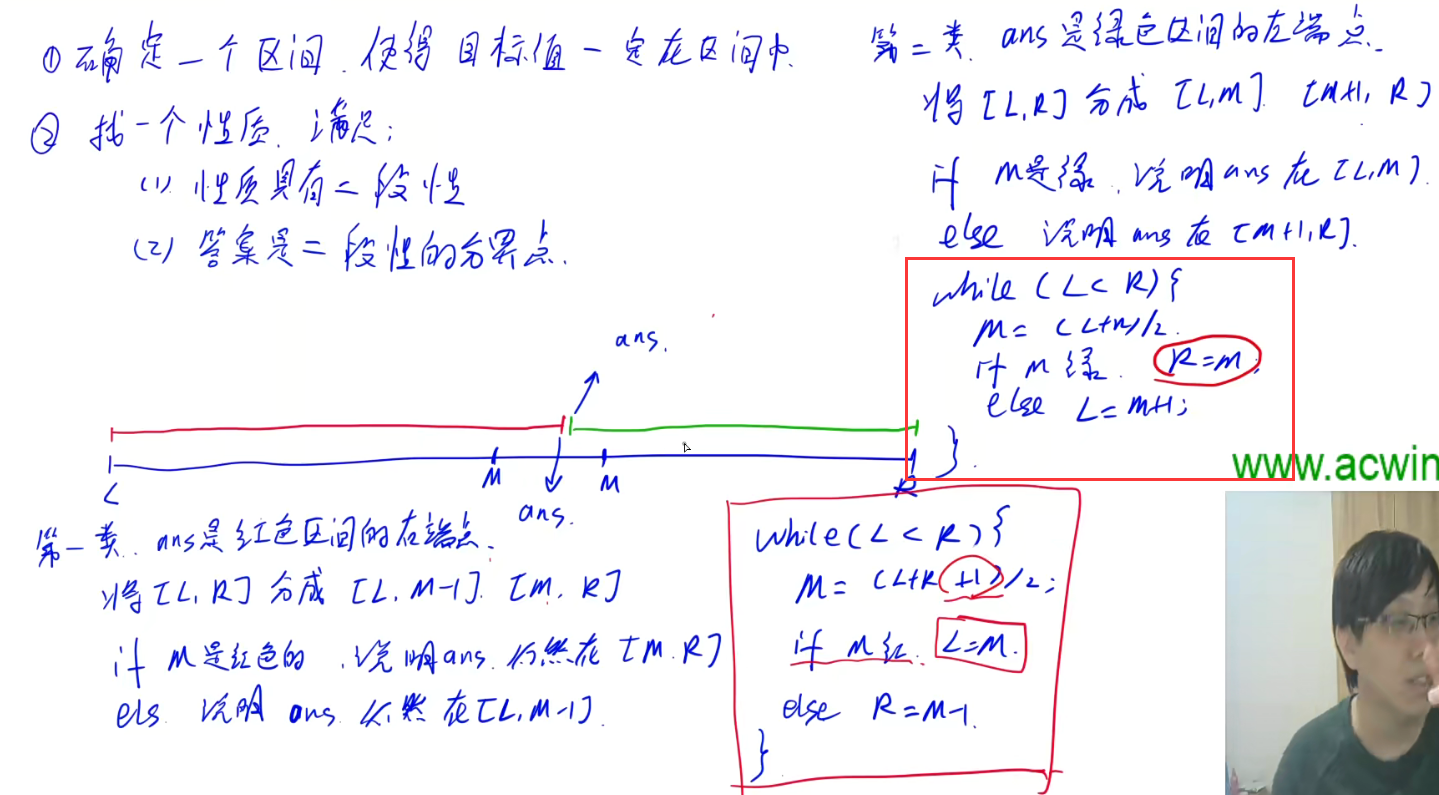
实数二分不需要考虑这些问题：

核心模板知识点

二分查找算法模板：y总总结。

• 闫总“二分查找算法”两个模板本质差别

若是区间为[l, mid]，[mid + 1, r]

// 区间[l, r]被划分成[l, mid]和[mid + 1, r]时使用：
while (l < r) {
    int mid = l + r >> 1;
    if (check(mid)) r = mid;
    else l = mid + 1;
}

若是区间为[l, mid - 1]，[mid, r]

// 区间[l, r]被划分成[l, mid - 1]和[mid, r]时使用：
while (l < r) {
    int mid = l + r >> 1;
    if (check(mid)) r = mid - 1;
    else l = mid;
}

例题

示例题目：704. 二分查找

题目内容：

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target  ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
    
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

提示：
你可以假设 nums 中的所有元素是不重复的。
n 将在 [1, 10000]之间。
nums 的每个元素都将在 [-9999, 9999]之间。

题目解决：

[l, mid],[mid + 1, r]情况：

class Solution {
 
    public boolean check(int mid, int target) {
        if (mid < target) return true;
        return false;
    }

    //-1,0,3,5,9,12
    //check：如果nums[mid] < target，l = mid + 1  否则  r = mid => [l, mid],[mid + 1, r] => mid = (l + r) / 2
    public int search(int[] nums, int target) {
        int l = 0, r = nums.length - 1;
        while (l < r) {
            int mid = l + r >> 1;
            if (check(nums[mid], target)) l = mid + 1;
            else r = mid;
        }
        return target == nums[l] ? l : -1;
    }
}

[l, mid - 1],[mid, r]情况：

class Solution {
 
    public boolean check(int mid, int target) {
        if (target < mid) return true;
        return false;
    }

    public int search(int[] nums, int target) {
        int l = 0, r = nums.length - 1;
        while (l < r) {
            int mid = l + r + 1 >> 1;
            if (check(nums[mid], target)) r = mid - 1;
            else l = mid;
        }
        return target == nums[l] ? l : -1;
    }
}

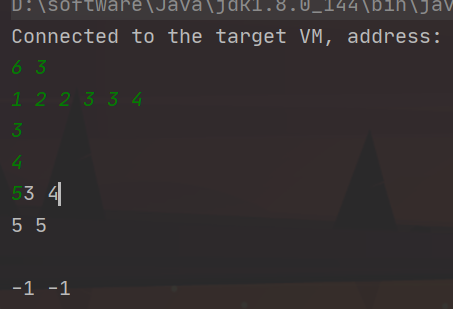
模板题：AcWing 789.数的范围

题目：Acwing 数的范围-二分算法-java实现

题目内容如下：

给定一个按照升序排列的长度为 n 的整数数组，以及 q 个查询。

对于每个查询，返回一个元素 k 的起始位置和终止位置（位置从 0 开始计数）。

如果数组中不存在该元素，则返回 -1 -1。

输入格式

第一行包含整数 n 和 q，表示数组长度和询问个数。
第二行包含 n 个整数（均在 1∼10000 范围内），表示完整数组。
接下来 q 行，每行包含一个整数 k，表示一个询问元素。

输出格式

共 q 行，每行包含两个整数，表示所求元素的起始位置和终止位置。
如果数组中不存在该元素，则返回 -1 -1。

数据范围

1≤n≤100000
1≤q≤10000
1≤k≤10000

输入样例

6 3
1 2 2 3 3 4
3
4
5

输出样例

3 4
5 5
-1 -1

题解

package com.changlu.java;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;

public class Main {

    private static int N = 100000;
    private static int n, q, target;
    private static int[] arr = new int[N];

    public static void main(String[] args) throws IOException {
        BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
        String[] s1 = cin.readLine().split(" ");
        n = Integer.parseInt(s1[0]);
        q = Integer.parseInt(s1[1]);
        String[] s2 = cin.readLine().split(" ");
        for (int i = 0; i < n; i++) {
            arr[i] = Integer.parseInt(s2[i]);
        }
        while (q != 0) {
            target = Integer.parseInt(cin.readLine());
            //开始找左边
            int l = 0, r = n - 1;
            while (l < r) {
                int mid = l + r >> 1;
                if (arr[mid] >= target) r = mid;
                else l = mid + 1;
            }
            if (arr[l] != target){
                System.out.printf("%d %d\n", -1, -1);
            }else {
                //确定最左边范围
                int left = l;
                l = 0;
                r = n - 1;
                //确认最右边范围
                while (l < r) {
                    int mid = l + r + 1 >> 1;
                    if (arr[mid] <= target) l = mid;
                    else r = mid - 1;
                }
                int right = l;
                System.out.printf("%d %d\n", left, right);
            }
            q--;
        }

    }
}

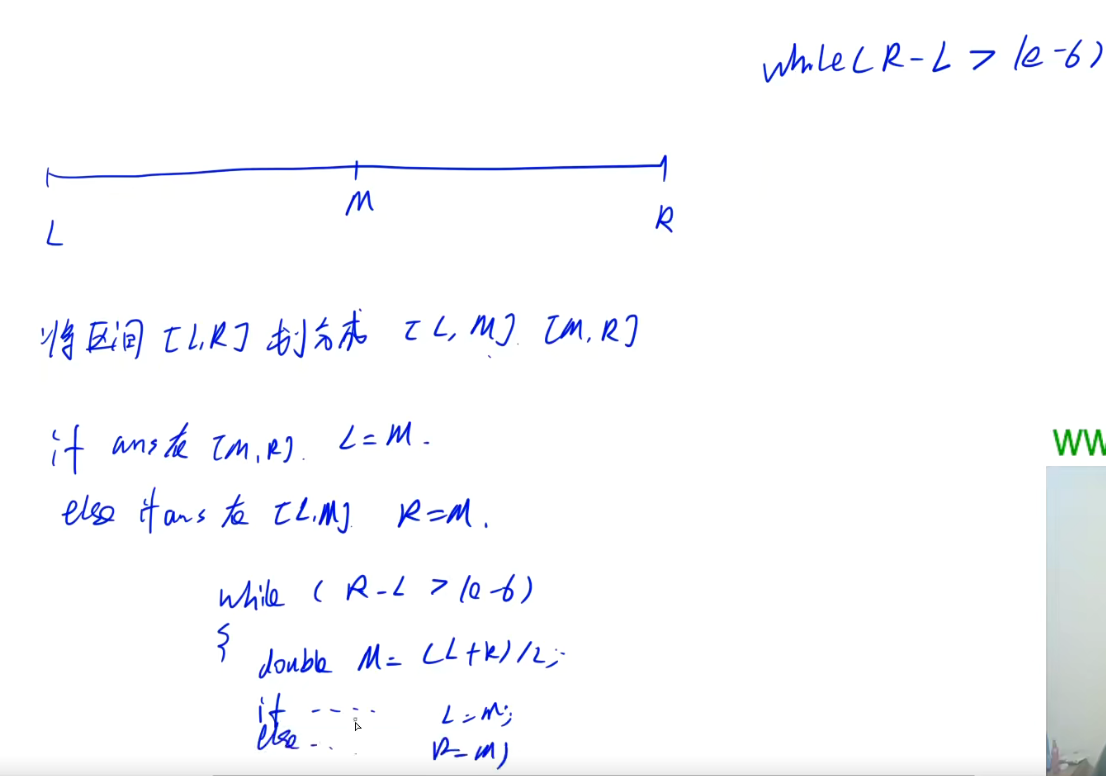
实数二分

知识点

模板题：AcWing 790.数的三次方根

题目链接：数的三次方根

代码模板：

bool check(double x) {/* ... */} // 检查x是否满足某种性质

double bsearch_3(double l, double r)
{
    const double eps = 1e-6;   // eps 表示精度，取决于题目对精度的要求
    while (r - l > eps)
    {
        double mid = (l + r) / 2;
        if (check(mid)) r = mid;
        else l = mid;
    }
    return l;
}

题目内容：Acwing 数的范围-二分算法-java实现

数的三次方根

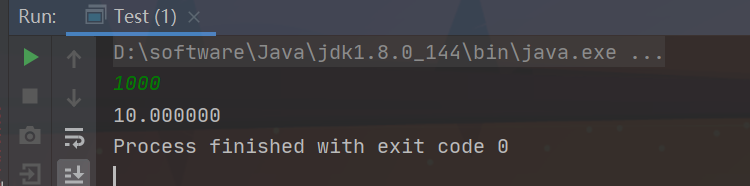
给定一个浮点数 n，求它的三次方根。

输入格式：共一行，包含一个浮点数 n。

输出格式：共一行，包含一个浮点数，表示问题的解。

注意，结果保留 6 位小数。

数据范围：−10000≤n≤10000

输入样例：1000.00
输出样例：10.000000

题解

首先题目给出保留6位小数，所以这里精度为6位

import java.util.*;
import java.io.*;

class Main{
    static double n;
    
    public static void main(String[] args)throws Exception{
        BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
        n = Double.valueOf(cin.readLine());
        double l = -10000, r = 10000;
        while (r - l > 1e-6) {
            double mid = (l + r) / 2;
            if (mid * mid * mid >= n) r = mid;
            else l = mid;
        }
        System.out.printf("%.6f", l);
    }
}

习题

题1：AcWing 730.机器人跳跃问题【中等】

来源：今日头条2019，笔试题

题目链接：730. 机器人跳跃问题

分析如下：

同样是采用二分来进行解决问题，比较核心的是在check函数中，我们对于mid >= 1e5情况时直接返回true，因为当满足该情况时，无需再进行往下递推去处理，因为一定是>0的。【若是不做该处理，可能会出现溢出出现负数的情况】

复杂度分析：时间复杂度O(nlogn)。计算一下：log(1e5)约等于30，接着30*1e5，此时就是300万，加上中间的一个剪枝处理，时间复杂度会进行优化。

import java.util.*;
import java.io.*;

class Main {
    
    static int n;
    static int[] h = new int[100010];
    //结果集
    static int res;
    
    //返回false表示当前的初始的高度不够
    public static boolean check(int mid) {
        for (int i = 0; i < n; i++) {
            mid = 2 * mid - h[i];
            if (mid < 0) return false;
            //若是mid>1e5，此时会不断的进行向上递增，因为若是下一次机器的高度就算是1e5，那么通过当前的mid两倍求得的结果依旧是>=1e5
            if (mid >= 1e5) return true;
        }
        return true;
    }
    
    public static void main(String[] args) throws Exception{
        BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
        n = Integer.valueOf(cin.readLine());
        String[] s = cin.readLine().split(" ");
        for (int i = 0; i < n; i++) {
            h[i] = Integer.valueOf(s[i]);
        }
        //接着来开始进行处理计算
        int l = 0, r = (int)1e5;
        while (l < r) {
            int mid = l + r >> 1;
            //符合条件尝试继续往前推举
            //[l, mid] [mid + 1, r]
            if (check(mid)) r = mid;
            else l = mid + 1;
        }
        System.out.printf("%d", l);
    }
}

题2：AcWing 1221.四平方和【简单，蓝桥杯题】

题目链接：1221. 四平方和

题解链接：AcWing 1221. 四平方和（每日一题·春季）

标签：暴力、二分(枚举的最大数)、哈希

思路：首先会去想枚举3个数字来去暴力求解，但是发现运算的次数为十几亿，这个时间复杂度肯定会超时，那么我们将其优化为枚举两个数字，首先去枚举b、d并且使用数组来存储起来它们的和与相应的数组。

1、借助map

//500 0000  平方 2200
//暴力 2000^3  60 0000 0000
//暴力 2000^2  400 0000

import java.util.*;
import java.io.*;

class Main {
    
    static class Pair<K, V>{
        K c;
        V d;
        public Pair(K c, V d) {
            this.c = c;
            this.d = d;
        }
    }
    
    private static int n;
    //记录两个合并值以及相对应的pair
    private static Map<Integer, Pair<Integer, Integer>> buckets = new HashMap<>();
    
    //注意：此题是从小到排序，那么就需要先将c、d预存起来，之后重新去枚举a、b即可求解
    public static void main(String[] args)throws Exception {
        BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
        n = Integer.valueOf(cin.readLine());
        for (int c = 0; c * c <= n; c++) 
            for (int d = c; d * d + c * c <= n; d++) {
                int sum = c * c + d * d;
                //若是存在直接输出
                if (!buckets.containsKey(sum)) {
                    //若是不存在来进行存储
                    buckets.put(sum, new Pair<Integer, Integer>(c, d));
                }
            }
        
        for (int a = 0; a * a <= n; a++)
            for (int b = a; b * b + a * a <= n; b++) {
                int coin = n - a * a - b * b;
                if (buckets.containsKey(coin)) {
                    Pair<Integer, Integer> pair = buckets.get(coin);
                    System.out.printf("%d %d %d %d", a, b, pair.c, pair.d);
                    return;
                }
            }
    }

}

2、数组来开辟空间（最优解）

//500 0000  平方 2200
//暴力 2000^3  60 0000 0000
//暴力 2000^2  400 0000

import java.util.*;
import java.io.*;

class Main {
    
    private static int N = (int)5e6 + 10;
    private static int n;
    //1千万个空间
    //各自存储相应的一个索引位置
    private static int[] C = new int[N], D = new int[N];
    
    //注意：此题是从小到排序，那么就需要先将c、d预存起来，之后重新去枚举a、b即可求解
    public static void main(String[] args)throws Exception {
        BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
        n = Integer.valueOf(cin.readLine());
        //填充-1
        Arrays.fill(C, -1);
        Arrays.fill(D, -1);
        //首先去枚举c、d
        for (int c = 0; c * c <= n; c++) 
            for (int d = c; d * d + c * c <= n; d++) {
                int sum = c * c + d * d;
                //若是存在直接输出
                if (C[sum] == -1) {
                    C[sum] = c;
                    D[sum] = d;
                }
            }
        
        //最后去枚举a、b
        for (int a = 0; a * a <= n; a++)
            for (int b = a; b * b + a * a <= n; b++) {
                int coin = n - a * a - b * b;
                if (C[coin] != -1) {
                    System.out.printf("%d %d %d %d", a, b, C[coin], D[coin]);
                    return;
                }
            }
    }

}

题3：AcWing 1227.分巧克力【简单，蓝桥杯题】

题目链接：1227. 分巧克力

分析：

一块巧克力（h[i]，k[i]）分割k.k大小的正方形小蛋糕，可以切得个数为：

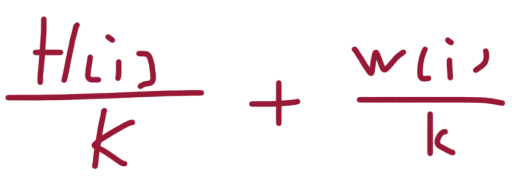
由题目得知，蛋糕的块数最大为100000块，也就是10万，题目需要让我们求得能够切得满足k块的最大巧克力方形边长。

暴力枚举的话就是对边长1-100000的进行暴力枚举10万块，时间复杂度为100000 x 100000 = 1千亿，绝对会超时，那么我们需要去降低复杂度。

这里我们可以发现，随着边长的增加，相应的块数一定会减少，对于单调性递增或递减的情况我们可以使用二分来进行解决：

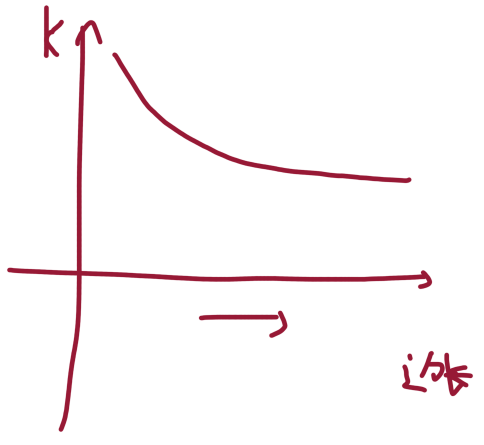
//mid指代当前切割蛋糕的数量，k指代题目要求的切割数量
//若是>=，表示还可能有更大的蛋糕边长可进行切割
若是mid >= k，l = mid
r = mid - 1

题解：

import java.util.*;
import java.io.*;

class Main {
    
    private static int N = (int)1e5 + 10;
    private static int n, k;
    private static int[] H = new int[N], W = new int[N];
    
    public static boolean check(int mid) {
        //遍历所有的蛋糕来查看当前的mid是否满足>=k
        int res = 0;
        for (int i = 0; i < n; i++) {
            res += (H[i] / mid) * (W[i] / mid);
            //若是中途有>=k，那么就返回true
            if (res >= k) return true;
        }
        return false;
    }
    
    public static void main(String[] args)throws Exception {
        BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
        //读取初始值
        String[] s = cin.readLine().split(" ");
        n = Integer.valueOf(s[0]);
        k = Integer.valueOf(s[1]);
        int i = 0;
        while (i < n) {
            String[] s1 = cin.readLine().split(" ");
            H[i] = Integer.valueOf(s1[0]);
            W[i] = Integer.valueOf(s1[1]);
            i++;
        }
        //定义左右边界（切割蛋糕的边长）
        int l = 0, r = (int)1e5;
        while (l < r) {
            int mid = l + r + 1 >> 1;
            if (check(mid)) l = mid;
            else r = mid - 1;
        }
        System.out.printf("%d", l);
    }
}

额外

leetcode：35. 搜索插入位置

class Solution {
    //mid >= target   r = mid
    //else l = mid + 1
    public int searchInsert(int[] nums, int target) {
        int l = 0, r = nums.length - 1;
        while (l < r) {
            int mid = (l + r) >> 1;
            //System.out.printf("%d, %d, %d\n", mid, l, r);
            if (nums[mid] >= target) r = mid;
            else l = mid + 1;
        }
        return l + (target > nums[l] ? 1 : 0);
    }
}

二、前缀和

知识点

简述：快速计算某一个区间内的前缀和，暂时不能够支持修改操作。

例如让你计算指定[i,j]区间的和，正常的思路就是首先计算[0, i]之间的和，接着计算[0, j]之间的和，最后将后者的和减去前者的和即可求得。

那么求区间的和时间复杂度为O(n)。

结论：使用前缀和实际上就是用空间来去优化时间复杂度，原本O(n)复杂度去优化为O(1)的复杂度，但是若是进行了修改操作，那么求区间值就会失效。

应用场景：多层for来进行优化，空间换时间。

模板题

一维前缀和：AcWing 795.前缀和

题目链接：acwing795：前缀和

题目内容：

题目内容：输入一个长度为n的整数序列。接下来再输入m个询问，每个询问输入一对l, r。对于每个询问，输出原序列中从第l个数到第r个数的和。

输入格式：
第一行包含两个整数n和m。
第二行包含n个整数，表示整数数列。
接下来m行，每行包含两个整数l和r，表示一个询问的区间范围。

输出格式:
共m行，每行输出一个询问的结果。

数据范围:
1≤l≤r≤n,
1≤n,m≤100000,
−1000≤数列中元素的值≤1000

输入输出样例：
样例输入1：
5 3
2 1 3 6 4
1 2
1 3
2 4

样例输出1：
3
9
10

题解模板：

import java.util.*;
import java.io.*;

class Main {
    private static final int N = 100010;
    private static int n, m;
    private static int []arr = new int[N];
    private static int []sum = new int[N];

    public static void main(String[] args)throws Exception {
        BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
        String[] s = cin.readLine().split(" ");
        n = Integer.valueOf(s[0]);
        m = Integer.valueOf(s[1]);
        s = cin.readLine().split(" ");
        for (int i = 1; i <= n; i++) {
            arr[i] = Integer.valueOf(s[i - 1]);
            //数组保存前缀和
            sum[i] = sum[i - 1] + arr[i];
        }
        while (m != 0) {
            s = cin.readLine().split(" ");
            //O(1)的时间复杂度计算区间值
            System.out.printf("%d\n", sum[Integer.valueOf(s[1]) + 1] - sum[Integer.valueOf(s[0]) + 1]);
            m--;
        }
    }
}

二维前缀和：AcWing 796.子矩阵的和

题目链接：acwing796：子矩阵的和

题目内容：

描述：输入一个n行m列的整数矩阵，再输入q个询问，每个询问包含四个整数x1, y1, x2, y2，表示一个子矩阵的左上角坐标和右下角坐标。
对于每个询问输出子矩阵中所有数的和。

输入格式：
第一行包含三个整数n，m，q。
接下来n行，每行包含m个整数，表示整数矩阵。
接下来q行，每行包含四个整数x1, y1, x2, y2，表示一组询问。

输出格式：
共q行，每行输出一个询问的结果。

数据范围：
1≤n,m≤1000,
1≤q≤200000,
1≤x1≤x2≤n,
1≤y1≤y2≤m,
−1000≤矩阵内元素的值≤1000

输入样例：
3 4 3
1 7 2 4
3 6 2 8
2 1 2 3
1 1 2 2
2 1 3 4
1 3 3 4

输出样例：
17
27
21

分析：两个公式分别推导

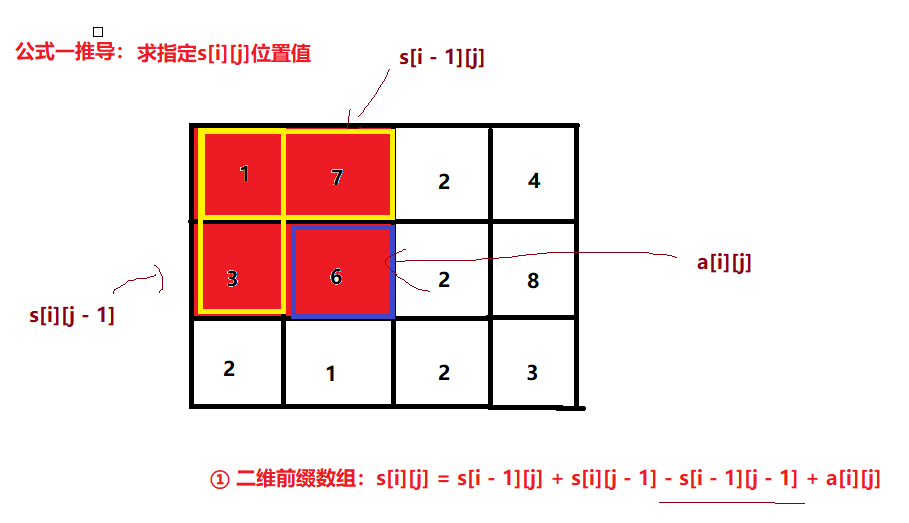
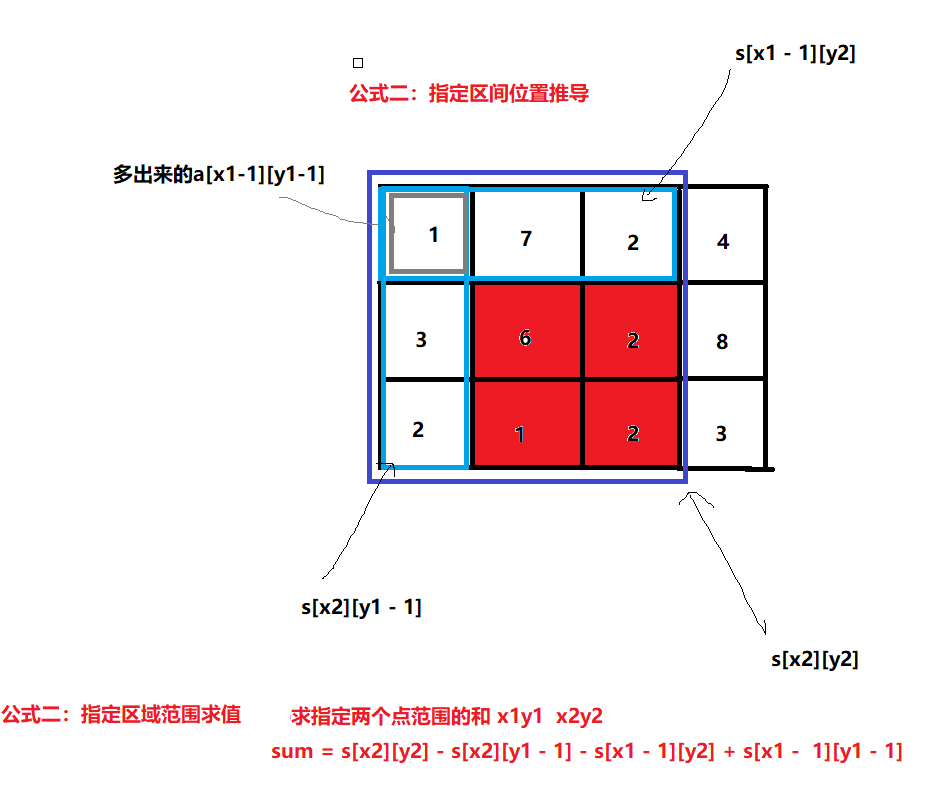
题解模板：

import java.util.*;
import java.io.*;

class Main {
    
    private static final int N = 1010;
    private static int n, m, q;
    private static int[][] arr = new int[N][N], sum = new int[N][N];

    public static void main(String[] args)throws Exception {
        BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
        String[] s = cin.readLine().split(" ");
        n = Integer.valueOf(s[0]);
        m = Integer.valueOf(s[1]);
        q = Integer.valueOf(s[2]);
        for (int i = 1; i <= n; i ++) {
            s = cin.readLine().split(" ");
            for (int j = 1; j <= m; j ++) {
                arr[i][j] = Integer.valueOf(s[j - 1]);
                sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + arr[i][j];
            }
        }
        while (q != 0) {
            s = cin.readLine().split(" ");
            int x1 = Integer.valueOf(s[0]);
            int y1 = Integer.valueOf(s[1]);
            int x2 = Integer.valueOf(s[2]);
            int y2 = Integer.valueOf(s[3]);
            System.out.printf("%d\n", sum[x2][y2] - sum[x2][y1 - 1] - sum[x1 - 1][y2] + sum[x1 - 1][y1 - 1]);
            q--;
        }
    }
}

---

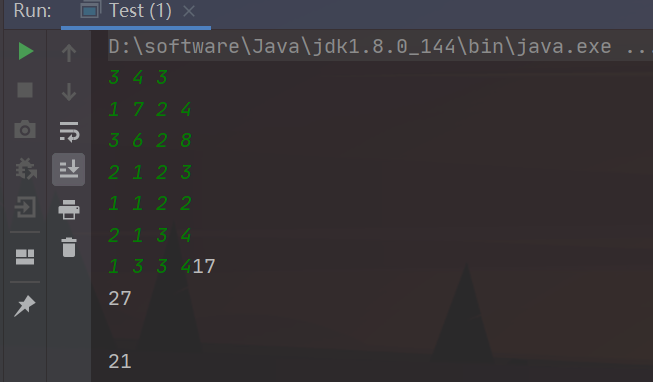
习题

题1：AcWing 99.激光炸弹【简单】

来源：《算法竞赛进阶指南》, HNOI2003

题目链接：99. 激光炸弹

标签：二维前缀和

分析：本道题实际上就是二维前缀和的一个应用。

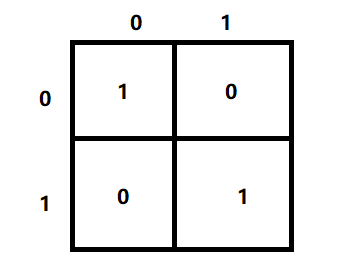
根据给出的输入样例，我们来进行分析一下：

2 1
0 0 1
1 1 1

//N表示目标xy以及相应w的值（对应下面有n行）  R表示爆照的正方形边长
N = 2   R = 1
x = 0  x = 0  w = 1
x = 1  y = 1  w = 1

对应输入案例的图如下：

接着读题，题目中说明了爆炸范围，即那个正方形的边必须和 x，y轴平行：

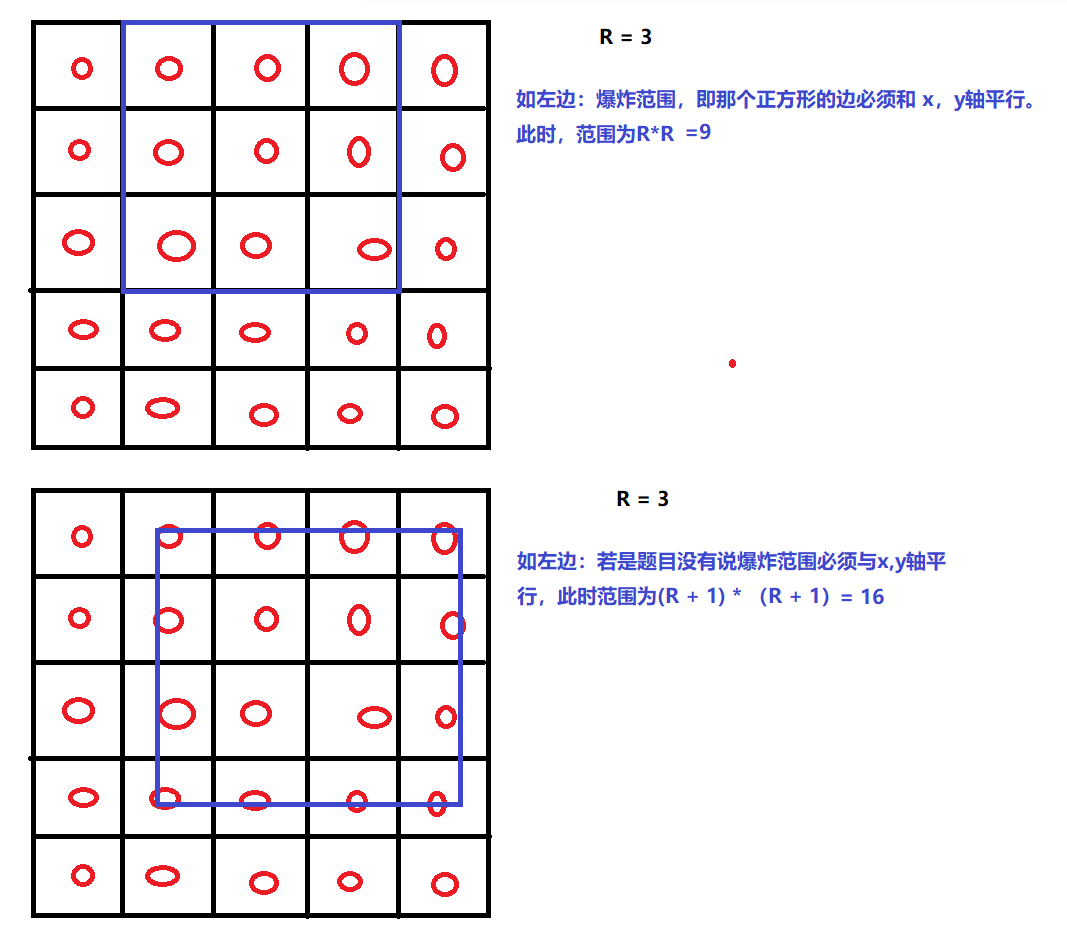
既然题目给我们确定的爆炸范围，也就是上图的第一个示例，那我们之后来计算二维前缀和时就有了确定的操作步骤。

注意点：

1、二维数组不能有两个，两个的话就会出现超限制内存的情况。

2、整个区域范围的长、宽一定要进行初始化，根据扫描的范围来设置初始值。

题解：

//R：正方形范围（炸弹范围）
//N：N个目标
//x,y表示坐标
//w：表示该坐标的的价值

//输入值对应内容
//2：目标数(N)  1：炸弹边长(R)
//对应的目标xy及价值

import java.util.*;
import java.io.*;

class Main {
    
    private static final int N = 5010;
    private static int n, r;
    //最大空间：2500 0000  //两千五百万，若是设置两个数组的话，那么就会为五千万，此时即有可能超过指定内存空间168MB
    //168MB => 4400万 【一个int 4个字节】
    private static int[][] arr = new int[N][N];//二维前缀数组同样借助arr表示
    
    public static void main (String[] args)throws Exception {
        BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
        String[] s = cin.readLine().split(" ");
        n = Integer.valueOf(s[0]);
        //由于最大的x,y范围为5000，那么实际上地图最大就是5000（题目中若是>5000，那么则使用5000的范围进行扫描）
        r = Math.min(5001, Integer.valueOf(s[1]));
        //自定义长、宽（根据扫描的范围作为初始值）
        int height = r, weight = r;
        while (n != 0) {
            s = cin.readLine().split(" ");
            int x = Integer.valueOf(s[0]) + 1;
            int y = Integer.valueOf(s[1]) + 1;
            int w = Integer.valueOf(s[2]);
            arr[x][y] += w;
            height = Math.max(height, x);
            weight = Math.max(weight, y);
            n--;
        }
        
        //构造前缀数组
        for (int i = 1; i <= height; i++) 
            for (int j = 1; j <= weight; j++) 
                arr[i][j] = arr[i][j - 1] + arr[i - 1][j] - arr[i - 1][j - 1] + arr[i][j];
        
        //来进行扫描，方形右下角(i, j)为准
        int res = 0;
        for (int i = r; i <= height; i++)
            for (int j = r; j <= weight; j++) 
                res = Math.max(res, arr[i][j] - arr[i][j - r] - arr[i - r][j] + arr[i - r][j - r]);
        System.out.printf("%d", res);
    }
}

---

题2：AcWing 1230.k倍区间【蓝桥杯，中等】

题目链接：1230.k倍区间

分析：

暴力枚举O(n^3^) => 优化（前缀和省去一个for循环）O(n^2^) => 存余数O(n)

下面是依次推举过程：

暴力枚举：O(n^3^)，10万.10万.10万 10^15^，绝对超时

//枚举左右端点
int res = 0;
for (int r = 1; r <= n; r++)  //右端点
    for (int l = 1; l <= r; l++) {  //左端点
     	int sum = 0;
        for (int i = l; i <= r; i++) sum += arr[i];
        if (sum % k == 0) res++;
    }

优化（借助前缀和，可进行优化区间），优化为O(n^2^)，此时为10^10^，10000 0000 00，一百亿也超时

s[]//前缀区间

int res = 0;
//枚举左右端点
for (int r = 1; r <= n; r++)  //右端点
    for (int l = 1; l <= r; l++) {  //左端点
     	int sum = s[r] - s[l];//借助前缀和快速求得区间
        if (sum % k == 0) res++;
    }

最终优化：时间复杂度O(n)，不超时

//我们拿到上面的一部分for循环
for (int l = 1; l <= r; l++) {  //左端点
    int sum = s[r] - s[l];//借助前缀和快速求得区间
    if (sum % k == 0) res++;
}

//上述代码我们简化一下，实际上是表示从1-r中找到(s[r] - s[l]) % k == 0的情况
//(s[r] - s[l]) % k == 0 可进行拆分 s[r] % k  -  s[l] % k == 0，实际上就是表示s[r] % k == s[l] % k
for (int l = 1; l <= r; l++) {  //左端点
    if (s[r] % k == s[l] % k) res++;
}

//二次简化下：从1-r中找到s[r] % k == s[l] % k的个数，由于这个r是不断进行变化的，若是变为r+1，那么此前的r个（s[r] % k实际上是无需进行重复计算的）
//我们来进行举例，例如：1-r => 1-3，s[r] % k == s[l] % k
s[3] % k == s[1] % k
s[3] % k == s[2] % k
s[3] % k == s[3] % k

//若是此时r+1，那么为1-4
s[4] % k == s[1] % k
s[4] % k == s[2] % k
s[4] % k == s[3] % k
S[4] % K == S[4] % K
此时你可以看到后面的s[1]%k、s[2]%k、s[3]%k，此前是已经进行求得过了
    
//如何基于此来进行优化呢？我们可再次使用一个cnt数组来保存%运算的结果
int res = 0;
cnt[0] = 1;//简化cnt[(int)(sum[0] % k)]++;
for (int r = 1; r <= n; r++) {
    res += cnt[s[r] % k];//获取1-(r-1)中与s[r] % k的结果匹配的个数，直接可类比for (int l = 1; l <= r; l++)
    cnt[s[r] % k]++;//对当前s[r] % k的计数+1，为之后提供匹配遍历
}

//下方是举例子
s[1] = 1 % 2 = 1
s[2] = 3 % 2 = 1
s[3] = 6 % 2 = 0
s[4] = 10 % 2 = 0
s[5] = 15 % 2 = 1

1-1
1([1,1])  1                                                              0
    
1-2
3([1,2])   2([2,2])  1  2                                                1
    
1-3
6([1,3])   5([2,3])   3([3,3])  1  2  3                                  1
    
1-4
10([1,4])  9([2,4])   7([3,4])   4([4,4]) 1 2 3 4                        2
    
1-5 
15([1,5])  14([2,5])  12([3,5])  9([4,5])   5([5,5])  1 2 3 4 5          2

题解：

import java.util.*;
import java.io.*;

class Main {
    
    private static final int N = 100010;
    private static int n, k;
    private static long[] sum = new long[N];//注意前缀和相加可能会爆int
    //保存临时%运算结果值得数量
    private static long[] cnt = new long[N];
    
    public static void main(String[] args)throws Exception {
        BufferedReader cin = new BufferedReader(new InputStreamReader(System.in));
        String[] s = cin.readLine().split(" ");
        n = Integer.valueOf(s[0]);
        k = Integer.valueOf(s[1]);
        //计算前缀和
        for (int i = 1; i <= n; i++){
            String numStr = cin.readLine();
            sum[i] = Integer.valueOf(numStr) + sum[i - 1];
        } 
        
        //计算k倍区间得个数
        long res = 0;
        cnt[0] = 1;//简化cnt[(int)(sum[0] % k)]++;
        for (int r = 1; r <= n; r++) {
            res += cnt[(int)(sum[r] % k)];
            cnt[(int)(sum[r] % k)]++;
        }
        System.out.printf("%d", res);
    }
}