@[toc]

前言

之后会参与leetcode周赛、双周赛，希望自己能够坚持下来，并以此来督促检验、提升自己的算法能力，加油！

第86场双周赛情况

地址：第310场周赛

战绩：

第三题案例超时了：

最后的情况：

目前竞赛分数：

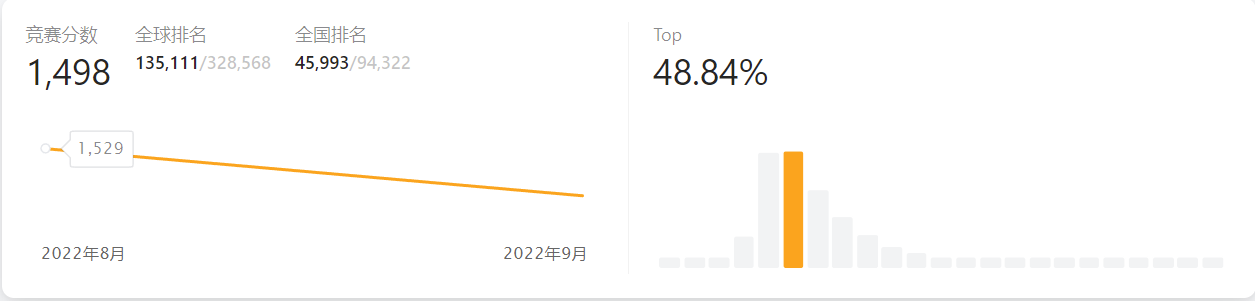
题目复盘+题解

题1：6176. 出现最频繁的偶数元素【easy】

题目链接：6176. 出现最频繁的偶数元素

题目内容：

给你一个整数数组 nums ，返回出现最频繁的偶数元素。
如果存在多个满足条件的元素，只需要返回 最小 的一个。如果不存在这样的元素，返回 -1 。

示例 1：
输入：nums = [0,1,2,2,4,4,1]
输出：2
解释：
数组中的偶数元素为 0、2 和 4 ，在这些元素中，2 和 4 出现次数最多。
返回最小的那个，即返回 2 。

示例 2：
输入：nums = [4,4,4,9,2,4]
输出：4
解释：4 是出现最频繁的偶数元素。

示例 3：
输入：nums = [29,47,21,41,13,37,25,7]
输出：-1
解释：不存在偶数元素。

提示：
1 <= nums.length <= 2000
0 <= nums[i] <= 105

思路：

1、哈希表+一遍遍历

复杂度分析：时间复杂度O(n)；空间复杂度O(n)

class Solution {
    
    public int mostFrequentEven(int[] nums) {
        int max = -1;
        int res = -1;
        Map<Integer, Integer> map = new HashMap<>();
        for (int num: nums) { 
            //偶数
            if ((num & 1) == 0) {
                int val = map.getOrDefault(num, 0) + 1;
                map.put(num, val);
                if (val == max && num < res) {
                    res = num;
                }
                if (val > max) {
                    max = val;
                    res = num;
                }
            }
        }
        return res;
    }
}

题2：6176. 出现最频繁的偶数元素【medium】

题目链接：6177. 子字符串的最优划分

题目内容：

给你一个字符串 s ，请你将该字符串划分成一个或多个 子字符串 ，并满足每个子字符串中的字符都是 唯一 的。也就是说，在单个子字符串中，字母的出现次数都不超过 一次 。
满足题目要求的情况下，返回 最少 需要划分多少个子字符串。
注意，划分后，原字符串中的每个字符都应该恰好属于一个子字符串。

示例 1：
输入：s = "abacaba"
输出：4
解释：
两种可行的划分方法分别是 ("a","ba","cab","a") 和 ("ab","a","ca","ba") 。
可以证明最少需要划分 4 个子字符串。

示例 2：
输入：s = "ssssss"
输出：6
解释：
只存在一种可行的划分方法 ("s","s","s","s","s","s") 。

提示：
1 <= s.length <= 105
s 仅由小写英文字母组成

思路：

1、滑动窗口+哈希表

复杂度分析：时间复杂度O(n)；空间复杂度O(1)

class Solution {
    public int partitionString(String s) {
        char[] arr = s.toCharArray();
        int[] tb = new int[26];
        int res = 0;
        for (int l = 0, r = 0; r < arr.length; r++) {
            if (tb[arr[r] - 'a'] == 1) {
                res++;
                //清理工作
                while (l < r) {
                    tb[arr[l] - 'a'] = 0;
                    l++;
                }
                //此时l == r
            }
            tb[arr[r] - 'a']++;
        }
        return res + 1;
    } 
}

题3：6178. 将区间分为最少组数【medium】

题目链接：6178. 将区间分为最少组数

题目内容：

给你一个二维整数数组 intervals ，其中 intervals[i] = [lefti, righti] 表示 闭 区间 [lefti, righti] 。
你需要将 intervals 划分为一个或者多个区间 组 ，每个区间 只 属于一个组，且同一个组中任意两个区间 不相交 。
请你返回 最少 需要划分成多少个组。
如果两个区间覆盖的范围有重叠（即至少有一个公共数字），那么我们称这两个区间是 相交 的。比方说区间 [1, 5] 和 [5, 8] 相交。

示例 1：
输入：intervals = [[5,10],[6,8],[1,5],[2,3],[1,10]]
输出：3
解释：我们可以将区间划分为如下的区间组：
- 第 1 组：[1, 5] ，[6, 8] 。
- 第 2 组：[2, 3] ，[5, 10] 。
- 第 3 组：[1, 10] 。
可以证明无法将区间划分为少于 3 个组。

示例 2：
输入：intervals = [[1,3],[5,6],[8,10],[11,13]]
输出：1
解释：所有区间互不相交，所以我们可以把它们全部放在一个组内。

提示：
1 <= intervals.length <= 105
intervals[i].length == 2
1 <= lefti <= righti <= 106

思路：

1、暴力法【超时，当时就卡住了】

复杂度分析：时间复杂度O(n^2^)；空间复杂度O(n)

public int minGroups(int[][] intervals) {
    Arrays.sort(intervals, (o1, o2)->o1[0] - o2[0]);
    boolean[] visited = new boolean[intervals.length];
    int res = 0;
    for (int i = 0; i < intervals.length; i++) {
        if (visited[i]) continue;
        int[] interval = intervals[i];
        for (int j = i + 1; j < intervals.length; j++) {
            if (intervals[j][0] > interval[1] && !visited[j]) {
                visited[j] = true;
                interval = intervals[j];
            }
        }
        res++;
    }
    return res;
}

2、小根堆+排序

复杂度分析：时间复杂度O(nlogn)；空间复杂度O(n)；

class Solution {

    //排序+小根堆
    public int minGroups(int[][] intervals) {
        //排序
        Arrays.sort(intervals, (o1, o2)->o1[0] - o2[0]);
        //小根堆（储存right的值）
        PriorityQueue<Integer> queue = new PriorityQueue<>();
        for (int[] arr: intervals) {
            if (!queue.isEmpty()) {
                //若是时间比最小的久那么就移除最小的，加入最新的实现一个替换
                if (arr[0] > queue.peek()) {
                    queue.poll();
                }
            }
            queue.offer(arr[1]);
        }
        return queue.size();
    }
}

复盘：当时根据开始时间排序是想到的，但是对应小根堆的一个贪心应用这个方式还是第一次碰到。

题4：6206. 最长递增子序列 II【hard，暂未ac】

题目链接：6206. 最长递增子序列 II

题目内容：

给你一个整数数组 nums 和一个整数 k 。
找到 nums 中满足以下要求的最长子序列：
子序列 严格递增
子序列中相邻元素的差值 不超过 k 。
请你返回满足上述要求的 最长子序列 的长度。
子序列 是从一个数组中删除部分元素后，剩余元素不改变顺序得到的数组。

示例 1：
输入：nums = [4,2,1,4,3,4,5,8,15], k = 3
输出：5
解释：
满足要求的最长子序列是 [1,3,4,5,8] 。
子序列长度为 5 ，所以我们返回 5 。
注意子序列 [1,3,4,5,8,15] 不满足要求，因为 15 - 8 = 7 大于 3 。

示例 2：
输入：nums = [7,4,5,1,8,12,4,7], k = 5
输出：4
解释：
满足要求的最长子序列是 [4,5,8,12] 。
子序列长度为 4 ，所以我们返回 4 。

示例 3：
输入：nums = [1,5], k = 1
输出：1
解释：
满足要求的最长子序列是 [1] 。
子序列长度为 1 ，所以我们返回 1 。

提示：
1 <= nums.length <= 105
1 <= nums[i], k <= 105

思路：①线段树。②树状数组。

题解暂时无，主要是目前还没有能力做出来这题，先这边标记下吧，花了一下午时间学了学线段树，不过对于该题题解还是没能够解出来。

学习索引：值域线段树（Python/Java/C++/Go）