@[toc]

前言

除了去年11月份以及今年近几月的算法刷题之外，只有在当时20年蓝桥杯准备的时候才刷过一些题，在当时就有接触到一些动归、递归回溯、贪心等等，不过那会也还是一知半解，做的题目也特别少，因为考虑到之后面试有算法题以及数据结构算法对于一个程序员十分重要，我也开始了刷题之路。

我目前的学习数据结构与算法及刷题路径：

1、学习数据结构的原理以及一些常见算法。

2、代码随想录：跟着这个github算法刷题项目进行分类刷，在刷题前可以学习一下对应类别的知识点，而且这里面每道题都讲的很详细。

3、牛客网高频面试101题：牛客网—面试必刷101题，在刷的过程中可以在leetcode同步刷一下。

4、接下来就是力扣上的专栏《剑指offer II》、《程序员面试金典（第 6 版）》…有对应的精选题单来对着刷即可。

5、大部分的高频面试、算法题刷完后，就可以指定力扣分类专栏进行一下刷题了。

刚开始刷的时候真的是很痛苦的，想到去年一道题可能就需要好几小时，真的就很难受的，不过熬过来一切都会好起来，随着题量的增多，很多题目你看到就会知道使用什么数据结构或者算法来去求解，并且思考对应的时间空间复杂度，并寻求最优解，我们一起加油！

我的刷题历程

截止2022.8.18：

1、牛客网101题(其中1题是平台案例有问题)：

2、剑指offerII：

力扣总记录数：

加油加油！

剑指offer

剑指 Offer 29. 顺时针打印矩阵【简单】

题目链接：剑指 Offer 29. 顺时针打印矩阵

题目内容：输入一个矩阵，按照从外向里以顺时针的顺序依次打印出每一个数字。

思路：

1、找规律，四个方位的下标不断进行平移

复杂度分析：

• 时间复杂度：O(n)
• 空间复杂度：O(n)

class Solution {
    //  1 2 3
    //  4 5 6
    //  7 8 9
    // 123（00、01、02）  69（12、22）  87（21、20）  4（10）  5（11）
    public int[] spiralOrder(int[][] matrix) {
        if (matrix == null || matrix.length == 0) {
            return new int[0];
        }
        int left = 0, right = matrix[0].length - 1, up = 0, down = matrix.length - 1;
        int num = (right + 1) * (down + 1);
        int[] nums = new int[num];
        int n = 0;
        while (true) {
            //遍历完第一行 up++
            for (int i = left; i <= right; i++) {
                nums[n++] = matrix[up][i];
            }
            up++;
            if (up > down) {
                break;
            }
            //遍历完最后一列 right--
            for (int i = up; i <= down; i++) {
                nums[n++] = matrix[i][right];
            }
            right--;
            if (right < left) {
                break;
            }
            //遍历完最后一行 down--
            for (int i = right; i >= left; i--) {
                nums[n++] = matrix[down][i];
            }
            down--;
            if (down < up) {
                break;
            }
            //遍历完第一列 left++
            for (int i = down; i >= up; i--) {
                nums[n++] = matrix[i][left];
            }
            left++;
            if (left > right) {
                break;
            }
        }
        return nums;
    }
}

---

剑指 Offer 66. 构建乘积数组【中等】

题目链接：剑指 Offer 66. 构建乘积数组

题目内容：给定一个数组 A[0,1,…,n-1]，请构建一个数组 B[0,1,…,n-1]，其中 B[i] 的值是数组 A 中除了下标 i 以外的元素的积, 即 B[i]=A[0]×A[1]×…×A[i-1]×A[i+1]×…×A[n-1]。不能使用除法。

思路：

1、乘积数组

复杂度分析：时间复杂度O(n)，空间复杂度O(1)，（数组 bb 作为返回值，不计入复杂度考虑）。

class Solution {
    //1 2 3 4 5
    //1 1 2 6 24 => 120 60 40 30 24，中间tmp作为乘数不断构建
    //核心不能够使用除法
    public int[] constructArr(int[] a) {
        if (a == null || a.length == 0) {
            return new int[0];
        }
        int[] b = new int[a.length];
        b[0] = 1;
        for (int i = 1; i < a.length; i++) {
            b[i] = b[i - 1] * a[i - 1];
        }
        int tmp = 1;
        for (int i = a.length - 2; i >= 0; i--) {
            tmp *= a[i + 1];
            b[i] = b[i] * tmp;
        }
        return b;
    }
}

牛客网

螺旋矩阵【简单】

题目链接：螺旋矩阵

题目内容：给定一个m x n大小的矩阵（m行，n列），按螺旋的顺序返回矩阵中的所有元素。

思路1：定义四个方向，left、right、up、down，然后不同方向进行遍历即可统一添加到list中。

复杂度分析：

• 时间复杂度：O(n)
• 空间复杂度：O(n)

import java.util.ArrayList;
public class Solution {
    //  1 2 3
    //  4 5 6
    //  7 8 9   //1236987456
    public ArrayList<Integer> spiralOrder(int[][] matrix) {
        ArrayList<Integer> res = new ArrayList<>();
        if (matrix == null || matrix.length == 0) {
            return res;
        }
        //定义四个位置
        int left = 0;
        int right = matrix[0].length - 1;
        int up = 0;
        int down = matrix.length - 1;
        while (left <= right && up <= down) {
            for (int i = left;i <= right;i++) {
                res.add(matrix[up][i]);
            }
            up++;
            if (up > down) {
                break;
            }
            for (int i = up;i <= down;i++) {
                res.add(matrix[i][right]);
            }
            right--;
            if (left > right) {
                break;
            }
            for (int i = right;i >= left;i--) {
                res.add(matrix[down][i]);
            }
            down--;
            if (up > down) {
                break;
            }
            for (int i = down;i >= up;i--) {
                res.add(matrix[i][left]);//注意注意
            }
            left++;
            if (left > right) {
                break;
            }
        }
        return res;
    }
}

LRU最近最少使用算法031【中等】

题目：设计LRU缓存结构

题目描述：

设计LRU(最近最少使用)缓存结构，该结构在构造时确定大小，假设大小为 capacity ，操作次数是 n ，并有如下功能:
1. Solution(int capacity) 以正整数作为容量 capacity 初始化 LRU 缓存
2. get(key)：如果关键字 key 存在于缓存中，则返回key对应的value值，否则返回 -1 。
3. set(key, value)：将记录(key, value)插入该结构，如果关键字 key 已经存在，则变更其数据值 value，如果不存在，则向缓存中插入该组 key-value ，如果key-value的数量超过capacity，弹出最久未使用的key-value

提示:
1.某个key的set或get操作一旦发生，则认为这个key的记录成了最常使用的，然后都会刷新缓存。
2.当缓存的大小超过capacity时，移除最不经常使用的记录。
3.返回的value都以字符串形式表达，如果是set，则会输出"null"来表示(不需要用户返回，系统会自动输出)，方便观察
4.函数set和get必须以O(1)的方式运行
5.为了方便区分缓存里key与value，下面说明的缓存里key用""号包裹

思路：

定义数据结构：双向链表以及一个哈希表
当前类需要的参数：一个头部结点、一个尾部结点、一个容量大小
核心两个方法：set()、get()方法
	set()：设置链表结点，①从缓存中取。②若是缓存中有，修改哈希表中的结点、移动结点到头部。③若是缓存中没有，判断新增一个是否超出容量大小，若没有超出，那么直接添加到链表头部；若是超出了，删除尾部结点，将新节点添加到头部。
	get()：从缓存中获取结点，若是没有直接返回null；若是有将结点移动至头部即可后返回。

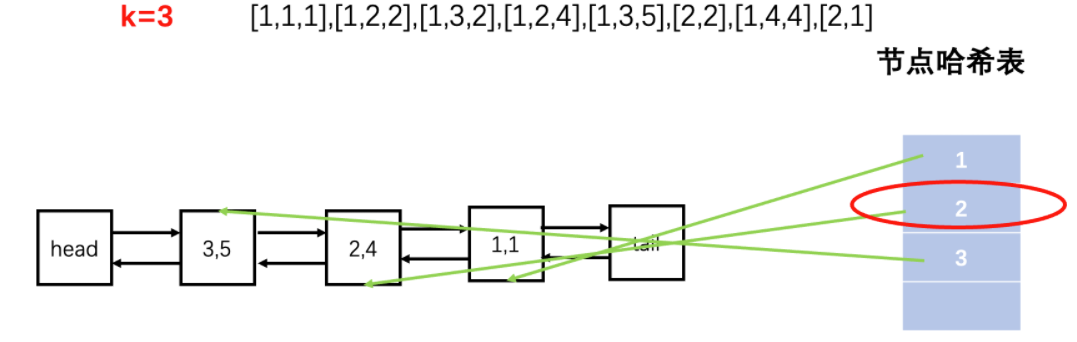
题解：

/**
 * @ClassName LRUCache
 * @Author ChangLu
 * @Date 4/21/2022 5:38 PM
 * @Description 最近最少使用LRU
 * 核心思路：①设置指定的容量。②hash存储缓存键值对。③链表来存储一个读取的顺序。（最新读的、修改的、创建的会放在head；新增容量满的话就会移除最后节点也就是最近最少读取的）
 */
public class Solution {
    
    class DLinkedNode{
        int key;
        int value;
        //定义一个前后指针
        DLinkedNode prev;
        DLinkedNode next;
        public DLinkedNode(){}
        public DLinkedNode(int _key, int _val) {
            this.key = _key;
            this.value = _val;
        }
    }
    
    //缓存
    private Map<Integer, DLinkedNode> cache = new HashMap<>();
    
    private int size;//当前的结点数量
    private int capacity;//容量大小
    //设置一个头尾结点
    private DLinkedNode head, tail;
    
    public Solution(int capacity) {
        this.size = 0;
        this.capacity = capacity;
        this.head = new DLinkedNode();
        this.tail = new DLinkedNode();
        this.head.next = this.tail;
        this.tail.prev = this.head;
    }

    public int get(int key) {
        //从缓存中取出节点
        DLinkedNode node = cache.get(key);
        if (node == null) {
            return -1;
        }
        //todo 实现函数
        moveToHead(node);//将结点移到链表的头部
        //返回值
        return node.value;
    }

    public void set(int key, int value) {
        DLinkedNode node = cache.get(key);
        if (node == null) {
            //插入该值
            DLinkedNode newNode = new DLinkedNode(key, value);
            //出现缓存已满情况
            if ((cache.size() + 1) > capacity) {
                //todo 移除底部的元素
                DLinkedNode delNode = removeTail();
                cache.remove(delNode.key);
            }
            //更新哈希表
            cache.put(key, newNode);
            //更新双向链表
            addToHead(newNode);
        }else {
            //修改该值，同样将其添加到顶部
            node.value = value;
            //todo 将结点添加到head头部
            moveToHead(node);
        }
    }
    
    //将结点移动至头部
    public void moveToHead(DLinkedNode node) {
        //删除该节点的指向
        removeNode(node);
        //最新结点的指向
        addToHead(node);
    }
    
    //将结点添加到头部
    public void addToHead(DLinkedNode node) {
        node.next = head.next;
        node.prev = head;
        head.next = node;
        node.next.prev = node;
    }
    
    //移除尾部结点
    public DLinkedNode removeTail() {
        DLinkedNode tailNode = tail.prev;
        removeNode(tailNode);
        return tailNode;
    }
    
    public void removeNode(DLinkedNode node){ 
        node.prev.next = node.next;
        node.next.prev = node.prev;
    }
    
}

设计LFU缓存结构【中等】

题目链接：设计LFU缓存结构

题目描述：每次移除最少使用的频率次数结点，若是频率相同，就再比较进入的先后

一个缓存结构需要实现如下功能。
set(key, value)：将记录(key, value)插入该结构
get(key)：返回key对应的value值
但是缓存结构中最多放K条记录，如果新的第K+1条记录要加入，就需要根据策略删掉一条记录，然后才能把新记录加入。这个策略为：在缓存结构的K条记录中，哪一个key从进入缓存结构的时刻开始，被调用set或者get的次数最少，就删掉这个key的记录；
如果调用次数最少的key有多个，上次调用发生最早的key被删除
这就是LFU缓存替换算法。实现这个结构，K作为参数给出

数据范围：0 < k \le 10^50<k≤10 
5
 ，|val| \le 2 \times 10^9∣val∣≤2×10 
9
 
要求：get和set的时间复杂度都是 O(logn)O(logn)，空间复杂度是 O(n)O(n)

思路1：

设计数据结构：
	一个Node类包含key、value、freq；
	设计两个哈希表：
		第一个是结点表`Map<int, Node>`（key表示结点的key）
		第二个是频率表`Map<int, LinkedList<Node>>`（int是频率，LinkedList中维护了对应的结点记录）
维护一个class变量minFreq：最小频率
整体思路：LFU核心思路就是淘汰最近最少频率使用的元素。

题解：

class LFUCache {

    class Node {
        int key;
        int value;
        int freq;
        public Node(){}
        public Node(int key, int value, int freq){
            this.key = key;
            this.value = value;
            this.freq = freq;
        }
    }

    //定义一个节点表
    private Map<Integer, Node> nodeTable = new HashMap<>();
    //定义一个频率表
    private Map<Integer, LinkedList<Node>> freqTable = new HashMap<>();
    //最小频率
    int minFreq;
    //可插入结点的容量数
    int capacity;

    public LFUCache(int capacity) {
        this.capacity = capacity;
    }
    
    public int get(int key) {
        //边界问题
        if (capacity == 0) {
            return -1;
        }
        //从缓存中获取节点
        Node node = nodeTable.get(key);
        //情况1：没有获取到
        if (node == null) {
            return -1;
        }
        //情况2：获取到了，此时就需要进行一次更新操作
        int nodeVal = node.value;
        //todo 更新频率
        updateFreq(node, key, nodeVal);
        return nodeVal;
    }
    
    public void put(int key, int value) {
        //边界问题
        if (capacity == 0) {
            return;
        }
        //从缓存中获取结点
        Node node = nodeTable.get(key);
        //情况1：获取到了，更新频率表 + 更新结点表
        if (node != null) {
            updateFreq(node, key, value);
            return;
        }
        //情况2：没有获取到，说明当前没有该结点，需要进行插入结点
        //判断当前是否可以插入到节点，若是插入不了结点需要进行移除最小频率的最少使用结点
        if ((nodeTable.size() + 1) > capacity) {
            //删除最小频率以及最少使用的节点
            Node removeNode = freqTable.get(minFreq).removeLast();
            //删除结点表中的节点
            nodeTable.remove(removeNode.key);
        }
        //进行新增操作
        minFreq = 1;
        //频率表新增
        LinkedList<Node> list = freqTable.getOrDefault(minFreq, new LinkedList<Node>());
        Node newNode = new Node(key, value, minFreq);
        list.addFirst(newNode);
        if (freqTable.get(minFreq) == null) {
            freqTable.put(minFreq, list);
        }
        //节点表新增
        nodeTable.put(key, newNode);
    }

    public void updateFreq(Node node, int key, int value) {
        //更新结点表
        node.value = value;
        //更新评率表
        int nodeFreq = node.freq;//当前待更新结点的频率
        LinkedList oldList = freqTable.get(nodeFreq);
        oldList.remove(node);//删除频率表中原先的结点
        //1、更新结点的频率信息
        int newNodeFreq = nodeFreq + 1;
        //更新最小频率（条件：①最小频率=节点频率。②结点频率的链表节点树为0。）
        if (minFreq == nodeFreq && oldList.size() == 0) {
            freqTable.remove(minFreq);
            minFreq = newNodeFreq;
        }
        node.freq = newNodeFreq;
        LinkedList nodeList = freqTable.getOrDefault(newNodeFreq, new LinkedList());
        nodeList.addFirst(node);
        if (freqTable.get(newNodeFreq) == null) {
            freqTable.put(newNodeFreq, nodeList);
        }
    }
    
}

旋转数组【中等】

题目链接：旋转数组

题目内容：一个数组A中存有 n 个整数，在不允许使用另外数组的前提下，将每个整数循环向右移 M（ M >=0）个位置，即将A中的数据由（A0 A1 ……AN-1 ）变换为（AN-M …… AN-1 A0 A1 ……AN-M-1 ）（最后 M 个数循环移至最前面的 M 个位置）。如果需要考虑程序移动数据的次数尽量少，要如何设计移动的方法？

思路1：三次反转。

• 第一次反转整个数组。第二次反转[0,m]位置。第三次反转[m, n - 1]位置，也就是后面剩余部分位置。

复杂度分析：

• 时间复杂度：O(n)
• 空间复杂度：O(1)

import java.util.*;


public class Solution {
    /**
     * 旋转数组
     * @param n int整型 数组长度
     * @param m int整型 右移距离
     * @param a int整型一维数组 给定数组
     * @return int整型一维数组
     */
    public int[] solve (int n, int m, int[] a) {
        m = m % n;//针对于超过a数组长度的情况
        //三次反转
        //6,2,123456 => 654321
        reverse(a, 0, n - 1);
        //654321 => 564321
        reverse(a, 0, m - 1);
        //564321 => 561234
        reverse(a, m, n - 1);
        return a;
    }
    
    //反转[i,j]的数组元素
    public void reverse(int[] a, int i, int j) {
        while (i < j) {
            int temp = a[i];
            a[i] = a[j];
            a[j] = temp;
            i++;
            j--;
        }
    }
    
}

顺时针旋转矩阵【中等】

题目链接：顺时针旋转矩阵

题目内容：有一个nxn整数矩阵，请编写一个算法，将矩阵顺时针旋转90度。给定一个nxn的矩阵，和矩阵的阶数n,请返回旋转后的nxn矩阵。

思路1：开辟新的数组，然后找规律即可。

复杂度分析：

• 时间复杂度：O(n^2^)
• 空间复杂度：O(n^2^)

import java.util.*;

public class Solution {
    public int[][] rotateMatrix(int[][] mat, int n) {
        int[][] temp = new int[n][n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                //画个图找规律即可
                temp[j][n - i - 1] = mat[i][j];
            }
        }
        return temp;
    }
}

思路2：直接在原始数组上来进行旋转，需要进行两次反转。

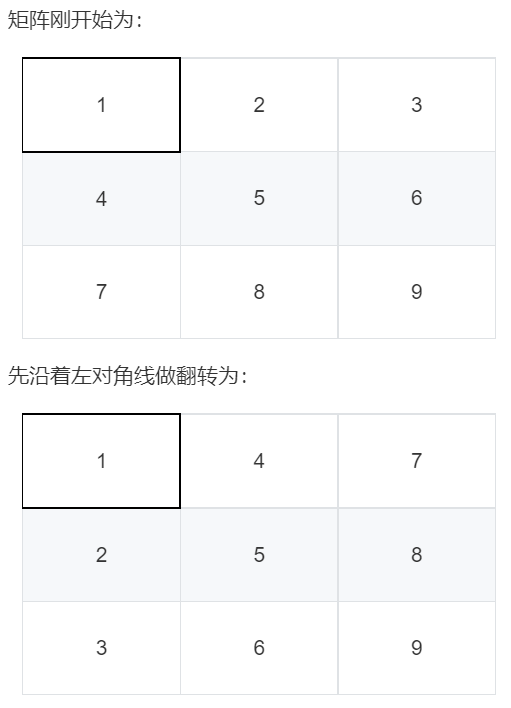
最后每行进行翻转：

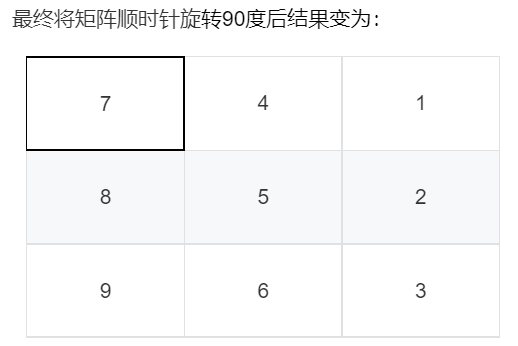
复杂度分析：

• 时间复杂度：O(n^2^)
• 空间复杂度：O(1)

import java.util.*;

public class Solution {
    public int[][] rotateMatrix(int[][] mat, int n) {
        //转换两遍
        //第一遍，对称交换
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < i; j++) {
                int temp = mat[i][j];
                mat[i][j] = mat[j][i];
                mat[j][i] = temp;
            }
        }
        //第二遍：每行的一维数组进行反转
        for (int i = 0; i < n; i++) {
            //写法1：
//             for (int j = 0; j < n / 2; j++) {
//                 int temp = mat[i][j];
//                 mat[i][j] = mat[i][n - j - 1];
//                 mat[i][n - j - 1] = temp;
//             }
            //写法2：翻转数组
            reverse(mat[i]);
        }
        return mat;
    }
    
    public void reverse(int[] nums) {
        int left = 0, right = nums.length - 1;
        while (left < right) {
            int temp = nums[left];
            nums[left] = nums[right];
            nums[right] = temp;
            left++;
            right--;
        }
    }
}