@[toc]

前言

除了去年11月份以及今年近几月的算法刷题之外，只有在当时20年蓝桥杯准备的时候才刷过一些题，在当时就有接触到一些动归、递归回溯、贪心等等，不过那会也还是一知半解，做的题目也特别少，因为考虑到之后面试有算法题以及数据结构算法对于一个程序员十分重要，我也开始了刷题之路。

我目前的学习数据结构与算法及刷题路径：

1、学习数据结构的原理以及一些常见算法。

2、代码随想录：跟着这个github算法刷题项目进行分类刷，在刷题前可以学习一下对应类别的知识点，而且这里面每道题都讲的很详细。

3、牛客网高频面试101题：牛客网—面试必刷101题，在刷的过程中可以在leetcode同步刷一下。

4、接下来就是力扣上的专栏《剑指offer II》、《程序员面试金典（第 6 版）》…有对应的精选题单来对着刷即可。

5、大部分的高频面试、算法题刷完后，就可以指定力扣分类专栏进行一下刷题了。

刚开始刷的时候真的是很痛苦的，想到去年一道题可能就需要好几小时，真的就很难受的，不过熬过来一切都会好起来，随着题量的增多，很多题目你看到就会知道使用什么数据结构或者算法来去求解，并且思考对应的时间空间复杂度，并寻求最优解，我们一起加油！

我的刷题历程

截止2022.8.18：

1、牛客网101题(其中1题是平台案例有问题)：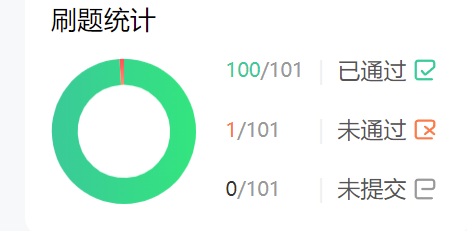

2、剑指offerII：

力扣总记录数：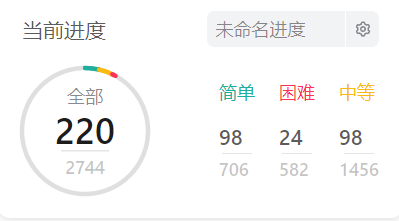

加油加油！

基础知识

回溯

1、什么是回溯法？

回溯法也可以叫做回溯搜索法，它是一种搜索的方式。

在二叉树系列中，我们已经不止一次，提到了回溯，例如二叉树：以为使用了递归，其实还隐藏着回溯 (opens new window)。

回溯是递归的副产品，只要有递归就会有回溯。

2、回溯法的效率？

回溯法的性能如何呢，这里要和大家说清楚了，虽然回溯法很难，很不好理解，但是回溯法并不是什么高效的算法。

因为回溯的本质是穷举，穷举所有可能，然后选出我们想要的答案，如果想让回溯法高效一些，可以加一些剪枝的操作，但也改不了回溯法就是穷举的本质。

那么既然回溯法并不高效为什么还要用它呢？

因为没得选，一些问题能暴力搜出来就不错了，撑死了再剪枝一下，还没有更高效的解法。

3、回溯法解决的问题？

回溯法，一般可以解决如下几种问题：

• 组合问题：N个数里面按一定规则找出k个数的集合
• 切割问题：一个字符串按一定规则有几种切割方式
• 子集问题：一个N个数的集合里有多少符合条件的子集
• 排列问题：N个数按一定规则全排列，有几种排列方式
• 棋盘问题：N皇后，解数独等等

相信大家看着这些之后会发现，每个问题，都不简单！

另外，会有一些同学可能分不清什么是组合，什么是排列？

组合是不强调元素顺序的，排列是强调元素顺序。

例如：{1, 2} 和 {2, 1} 在组合上，就是一个集合，因为不强调顺序，而要是排列的话，{1, 2} 和 {2, 1} 就是两个集合了。

记住组合无序，排列有序，就可以了。

4、如何理解回溯？

回溯法解决的问题都可以抽象为树形结构，是的，我指的是所有回溯法的问题都可以抽象为树形结构！

因为回溯法解决的都是在集合中递归查找子集，集合的大小就构成了树的宽度，递归的深度，都构成的树的深度。

递归就要有终止条件，所以必然是一颗高度有限的树（N叉树）。

这块可能初学者还不太理解，后面的回溯算法解决的所有题目中，我都会强调这一点并画图举相应的例子，现在有一个印象就行。

回溯法模板

起名：backtracking

1、回溯算法中函数返回值一般为void。

2、参数：因为回溯算法需要的参数可不像二叉树递归的时候那么容易一次性确定下来，所以一般是先写逻辑，然后需要什么参数，就填什么参数。

3、终止条件：什么时候达到了终止条件，树中就可以看出，一般来说搜到叶子节点了，也就找到了满足条件的一条答案，把这个答案存放起来，并结束本层递归。

回溯搜索的遍历过程：在上面我们提到了，回溯法一般是在集合中递归搜索，集合的大小构成了树的宽度，递归的深度构成的树的深度。

回溯法解决的问题都可以抽象为树形结构（N叉树）。

模板框架：

void backtracking(参数) {
    if (终止条件) {
        存放结果;
        return;
    }

    for (选择：本层集合中元素（树中节点孩子的数量就是集合的大小）) {
        处理节点;
        backtracking(路径，选择列表); // 递归
        回溯，撤销处理结果
    }
}

剑指offer

剑指 Offer 17. 打印从1到最大的n位数【简单】

题目链接：剑指 Offer 17. 打印从1到最大的n位数

题目内容：输入数字 n，按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3，则打印出 1、2、3 一直到最大的 3 位数 999。

思路：

1、迭代计算

复杂度分析：

• 时间复杂度：O(n)
• 空间复杂度：O(1)

class Solution {
    public int[] printNumbers(int n) {
        int num = 1;
        for (int i = 1; i <= n; i++) {
            num *= 10;
        }
        int[] res = new int[num - 1];
        for (int i = 1; i < num; i++) {
            res[i - 1] = i;
        }
        return res;
    }
}

本题实际上核心考察的是大数问题，只不过题目并没有出清楚。

思路：dfs+回溯

class Solution {
    
	private char[] nums = new char[]{'0', '1', '2', '3', '4', '5', '6', '7', '8', '9'};
    private List<String> res;
    private StringBuilder str;

    //n表示几位数
    //示例：1、2、3、4...99
    public List<String> printNumbers(int n) {
        res = new ArrayList<>();
        str = new StringBuilder();
        for (int i = 1; i <= n; i++) {
            dfs(0, i);
        }
        return res;
    }

    /**
     * x表示当前是第几位，len表示有多少位
     * @param x
     * @param len
     */
    public void dfs(int x, int len) {
        if (x == len) {
            res.add(str.toString());
            return;
        }
        int start = x == 0 ? 1 : 0;
        for (int i = start; i < nums.length; i++) {
            str.append(nums[i]);
            dfs(x + 1, len);
            str.deleteCharAt(str.length() - 1);
        }
    }
    
    public static void main(String[] args) {
        Test test = new Test();
        List<String> s = test.printNumbers(5);
        System.out.println(s);
    }
}

---

剑指 Offer 12. 矩阵中的路径【简单】

题目链接：剑指 Offer 12. 矩阵中的路径

题目内容：给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

思路：

1、dfs+回溯+剪枝

复杂度分析：

• 时间复杂度O(3^k^.MN)，3指的就是上下左右四个方向舍去回头方向，k为字符串长度，MN就是矩阵数量。
• 空间复杂度：O(K)，递归深度不会超过k长度。

class Solution {
    public boolean exist(char[][] board, String word) {
        if (board == null) {
            return false;
        }
        char[] wordArr = word.toCharArray();
        //所有位置都可以看作是起点
        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board[i].length; j++) {
                if (dfs(board, wordArr, i, j, 0)) {
                    return true;
                }
            }
        }
        return false;
    }

    public boolean dfs(char[][] board, char[] word, int i, int j, int k) {
        //边界条件，以及当前是否已经访问过
        if (i < 0 || i >= board.length || j < 0 || j >= board[i].length || board[i][j] != word[k]) {
            return false;
        }
        //若是此时k已经到末尾了,表示符合条件
        if (k == word.length - 1){
            return true;
        }
        //覆盖当前的元素
        board[i][j] = '1';
        boolean res = dfs(board, word, i + 1, j, k + 1) || dfs(board, word, i - 1, j, k + 1) ||
                      dfs(board, word, i, j + 1, k + 1) || dfs(board, word, i, j - 1, k + 1);
        //回溯（能够从第一个if中过去的，肯定是board[i][j] = word[k]的，所以这里可以直接进行回溯）
        board[i][j] = word[k];
        return res;
    }
}

---

剑指 Offer 64. 求1+2+…+n【中等】

题目链接：剑指 Offer 64. 求1+2+…+n

题目内容：求 1+2+...+n ，要求不能使用乘除法、for、while、if、else、switch、case等关键字及条件判断语句（A?B:C）。

思路：数学运算或者递归。

1、乘除法

复杂度分析：时间复杂度O(n)、空间复杂度O(1)

class Solution {
    public int sumNums(int n) {
        return (n + 1) * n / 2;
    }
}

2、递归

复杂度分析：时间复杂度O(n)、空间复杂度O(n)

递归的话需要你判断得到一个出口，又题目不给你if，如何解决？

①通过异常捕捉

class Solution {
    public int sumNums(int n) {
        try {
            int a = 1 / n;
        }catch(Exception e) {
            return 0;
        }
        return n + sumNums(n - 1);
    }
}

②通过与运算

class Solution {
    public int sumNums(int n) {
        //将n > 1作为放行条件，利用&运算来控制右边是否执行，当n=0时，此时会直接返回n
        boolean flag = n > 1 && (n += sumNums(n - 1)) > 0;
        return n;
    }
}

---

剑指 Offer 49. 丑数【中等】

题目链接：剑指 Offer 49. 丑数

题目内容：我们把只包含质因子 2、3 和 5 的数称作丑数（Ugly Number）。求按从小到大的顺序的第 n 个丑数。

思路：

1、动态规划

状态定义：dp[i]，i表示第i+1的丑数值
转移方程：dp[i]=min(dp[a]×2,dp[b]×3,dp[c]×5) 
	需要维护a、b、c三个索引
初始化状态：dp[0]=1
返回值：dp[n-1]

复杂度分析：时间复杂度O(n)、空间复杂度O(1)

class Solution {
    public int nthUglyNumber(int n) {
        int a = 0, b = 0, c = 0;
        int[] dp = new int[n];
        //初始化
        dp[0] = 1;
        //实际上过程中枚举了所有的丑数情况
        for (int i = 1; i < n; i++) {
            int num2 = dp[a] * 2, num3 = dp[b] * 3, num5 = dp[c] * 5;
            dp[i] = Math.min(Math.min(num2, num3), num5);
            //计数+1（只要是相等数的情况，那么就需要加一，防止出现重复）
            if (dp[i] == num2) {
                a++;
            }
            if (dp[i] == num3) {
                b++;
            }
            if (dp[i] == num5){
                c++;
            }
        }
        return dp[n - 1];
    }
}

---

牛客网

斐波那契数列【入门】

题目链接：斐波那契数列

题目内容：大家都知道斐波那契数列，现在要求输入一个正整数 n ，请你输出斐波那契数列的第 n 项。斐波那契数列是一个满足 fib(x)=\left{ \begin{array}{rcl} 1 & {x=1,2}\ fib(x-1)+fib(x-2) &{x>2}\ \end{array} \right.fib(x)={1fib(x−1)+fib(x−2)x=1,2x>2 的数列数据范围：1\leq n\leq 401≤n≤40 要求：空间复杂度 O(1)O(1)，时间复杂度 O(n)O(n) ，本题也有时间复杂度 O(logn)O(log**n) 的解法

思路1：迭代

复杂度分析：

• 时间复杂度：O(n)
• 空间复杂度：O(1)

public class Solution {
    public int Fibonacci(int n) {
        int ans = 1;
        int a = 1;
        int b = 1;
        for (int i = 2;i < n;i++) {
            ans = a + b;
            a = b;
            b = ans;
        }
        return ans;
    }
}

没有重复项数字的全排列【中等】

题目链接：没有重复项数字的全排列

题目内容：给出一组数字，返回该组数字的所有排列

思路1：全排列递归方案。

复杂度分析：

• 时间复杂度:[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-8BKt3Gbz-1660906308930)(https://www.nowcoder.com/equation?tex=O(n * n!)]&preview=true)。n为num数组的长度。
• 空间复杂度:[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VmfW8KeF-1660906308930)(https://www.nowcoder.com/equation?tex=O(n)]&preview=true)。返回的结果的空间。

import java.util.*;

public class Solution {
    
    //结果集
    private ArrayList<ArrayList<Integer>> res = new ArrayList<ArrayList<Integer>>();
    
    public ArrayList<ArrayList<Integer>> permute(int[] num) {
        LinkedList<Integer> list = new LinkedList<>();
        recurison(num, list);
        return res;
    }
    
    public void recurison(int[] num, LinkedList<Integer> list) {
        //出口
        if (list.size() == num.length) {
            res.add(new ArrayList<>(list));
            return;
        }
        //全排列方案列举
        for (int i = 0; i < num.length; i++) {
            //过滤掉重复项
            if (list.contains(num[i])) {
                continue;
            }
            list.add(num[i]);
            //递归处理
            recurison(num, list);
            //为了方便删除最后一个元素，所以选中LinkedList
            list.removeLast(); 
        }
    }
    
}

思路2（推荐）：优化思路1，其中的判断某个值在集合中是否存在，采用空间换时间的思路，使用一个visted数组来进行表示状态。

class Solution {

    //结果集
    private List<List<Integer>> res = new ArrayList<List<Integer>>();

    public List<List<Integer>> permute(int[] nums) {
        ArrayList<Integer> list = new ArrayList<>();
        recursion(nums, list, new boolean[nums.length]);
        return res;
    }

    public void recursion(int[] nums, ArrayList<Integer> list, boolean[] visited) {
        if (list.size() == nums.length) {
            res.add(new ArrayList<>(list));
            return;
        }
        for (int i = 0; i < nums.length; i++) {
            //优化处：使用一个boolean数组来表示该元素是否访问过状态
            if (visited[i]) {
                continue;
            }
            list.add(nums[i]);
            visited[i] = true;
            recursion(nums, list, visited);
            list.remove(list.size() - 1);
            visited[i] = false;
        }
    }

}

有重复项数字的全排列【中等】

题目链接：有重复项数字的全排列

题目内容：给出一组可能包含重复项的数字，返回该数字的非重复排列。结果以字典升序排列。

思路1：在本章节牛客网题目1优化题解中修改两处即可解决

复杂度分析：

• 时间复杂度:O(n×n!)，其中 n 为数组的长度。
• 空间复杂度:O(n)。返回的结果。

import java.util.*;

public class Solution {
    
    //结果集
    private ArrayList<ArrayList<Integer>> res = new ArrayList<ArrayList<Integer>>();
    
    public ArrayList<ArrayList<Integer>> permuteUnique(int[] nums) {
        ArrayList<Integer> list = new ArrayList<>();
        //修改操作2：对nums排序
        Arrays.sort(nums);
        recursion(nums, list, new boolean[nums.length]);
        return res;
    }
    
    public void recursion(int[] nums, ArrayList<Integer> list, boolean[] visited) {
        if (list.size() == nums.length) {
            res.add(new ArrayList<>(list));
            return;
        }
        for (int i = 0; i < nums.length; i++) {
            //修改操作1：
            //i > 0 && nums[i] == nums[i - 1] && !visited[i]处理的是递归下去情况中出现重复的排列情况
            //举例：112   第一轮：112 121  第二轮的第一个数字，此时为1，visited[1]为false，此时重点来了看后面的条件，若是当前值与之前的相同并且前面的此时并没有访问过，那么跳过这个情况
            if (visited[i] || (i > 0 && nums[i] == nums[i - 1] && !visited[i - 1])) {
                continue;
            }
            list.add(nums[i]);
            visited[i] = true;
            recursion(nums, list, visited);
            list.remove(list.size() - 1);
            visited[i] = false;
        }
    }
}

岛屿数量【中等】

题目链接：岛屿数量

题目内容：给一个01矩阵，1代表是陆地，0代表海洋， 如果两个1相邻，那么这两个1属于同一个岛。我们只考虑上下左右为相邻。岛屿: 相邻陆地可以组成一个岛屿（相邻:上下左右） 判断岛屿个数。

思路1：dfs，通过消减方法来解决，递归操作是将临近得上下左右1->0。

复杂度分析：

• 时间复杂度：O(m*n)
• 空间复杂度：O(m*n)

import java.util.*;


public class Solution {
    
    public void dfs(char[][] grid, int i, int j) {
        //进行1->0
        grid[i][j] = '0';
        //四个方法进行递归操作
        //上
        if (i - 1 >= 0 && grid[i - 1][j] == '1') {
            dfs(grid, i - 1, j);
        }
        //下
        if (i + 1 < grid.length && grid[i + 1][j] == '1') {
            dfs(grid, i + 1, j);
        }
        //左
        if (j - 1 >= 0 && grid[i][j - 1] == '1') {
            dfs(grid, i, j - 1);
        }
        //右
        if (j + 1 < grid[i].length && grid[i][j + 1] == '1') {
            dfs(grid, i, j + 1);
        }
    }
    
    /**
     * 判断岛屿数量
     * @param grid char字符型二维数组 
     * @return int整型
     */
    //思路：采用消减法
    public int solve (char[][] grid) {
        int count = 0;
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[i].length; j++) {
                if (grid[i][j] == '1') {
                    count++;
                    //递归：消减
                    dfs(grid, i, j);
                }
            }
        }
        return count;
    }
}

思路2：bfs，利用队列来进行推断周边是否为岛屿。

复杂度分析：

• 时间复杂度：O(m*n)
• 空间复杂度：O(min(m, n))

import java.util.*;


public class Solution {
    
    class Pos {
        public int i;
        public int j;
        public Pos(int i, int j) {
            this.i = i;
            this.j = j;
        }
    }
    
    /**
     * 判断岛屿数量
     * @param grid char字符型二维数组 
     * @return int整型
     */
    //bfs
    public int solve (char[][] grid) {
        int count = 0;
        //队列存储坐标
        Deque<Pos> queue = new LinkedList<>();
        for (int i = 0; i < grid.length; i++) {
            for (int j = 0; j < grid[i].length; j++) {
                if (grid[i][j] == '1') {
                    count++;
                    grid[i][j] = '0';
                    //将对应得坐标添加到队列中
                    queue.offer(new Pos(i , j));
                    while (!queue.isEmpty()) {
                        //获取到队列中得一个结点
                        Pos pos = queue.poll();
                        int x = pos.i;
                        int y = pos.j;
                        //四个方向来进行试探
                        //上
                        if (x - 1 >= 0 && grid[x - 1][y] == '1') {
                            grid[x - 1][y] = '0';
                            queue.offer(new Pos(x-1, y));
                        }
                        //下
                        if (x + 1 < grid.length && grid[x + 1][y] == '1') {
                            grid[x + 1][y] = '0';
                            queue.offer(new Pos(x+1, y));
                        }
                        //左
                        if (y - 1 >= 0 && grid[x][y - 1] == '1') {
                            grid[x][y - 1] = '0';
                            queue.offer(new Pos(x, y - 1));
                        }
                        //右
                        if (y + 1 < grid[i].length && grid[x][y + 1] == '1') {
                            grid[x][y + 1] = '0';
                            queue.offer(new Pos(x, y + 1));
                        }
                    }
                }
            }
        }
        return count;
    }
}

字符串的排列【中等】

牛客网代码不通过

题目链接：字符串的排列

题目内容：输入一个长度为 n 字符串，打印出该字符串中字符的所有排列，你可以以任意顺序返回这个字符串数组。例如输入字符串ABC,则输出由字符A,B,C所能排列出来的所有字符串ABC,ACB,BAC,BCA,CBA和CAB。

dfs递归拼接：

import java.util.*;

public class Solution {
    
    private ArrayList<String> list = new ArrayList<>();
    
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param str string字符串 
     * @return string字符串ArrayList
     */
    public ArrayList<String> Permutation (String str) {
        char[] chars = str.toCharArray();
        Arrays.sort(chars);
        dfs(new StringBuilder(), chars, new boolean[str.length()]);
        return list;
    }
    
    public void dfs(StringBuilder builder, char[] chars, boolean visited[]) {
        if (builder.length() == chars.length) {
            list.add(builder.toString());
            return;
        }
        for (int i = 0; i < chars.length; i++) {
            if (visited[i] || (i > 0 && chars[i] == chars[i - 1] && !visited[i - 1])) {
                continue;
            }
            builder.append(chars[i]);
            visited[i] = true;
            dfs(builder, chars, visited);
            //回溯
            builder.deleteCharAt(builder.length() - 1);
            visited[i] = false;
        }
    }
    
}

swap交换方式：

import java.util.*;


public class Solution {
    
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param str string字符串 
     * @return string字符串ArrayList
     */
    public ArrayList<String> Permutation (String str) {
        char[] ch = str.toCharArray();
        ArrayList<String> list = new ArrayList<>();
        fun(list, ch, 0);
        return list;
    }
    
    public void fun(ArrayList<String> list, char[] chars,int index) {
        if (index == chars.length) {
            String str = new String(chars);
            if (!list.contains(str)) {
                list.add(str);
            }
        }else {
            for (int j = index; j < chars.length; j++) {
                swap(chars, index, j);
                fun(list, chars, index + 1);
                swap(chars, index, j);
            }
        }
    }
    
    public void swap(char[] chars, int i, int j) {
        if (i != j) {
            char temp = chars[i];
            chars[i] = chars[j];
            chars[j] = temp;
        }
    }
    
}

优化算法：

1、通过使用剪枝来进行删减掉重复得字符，如下。

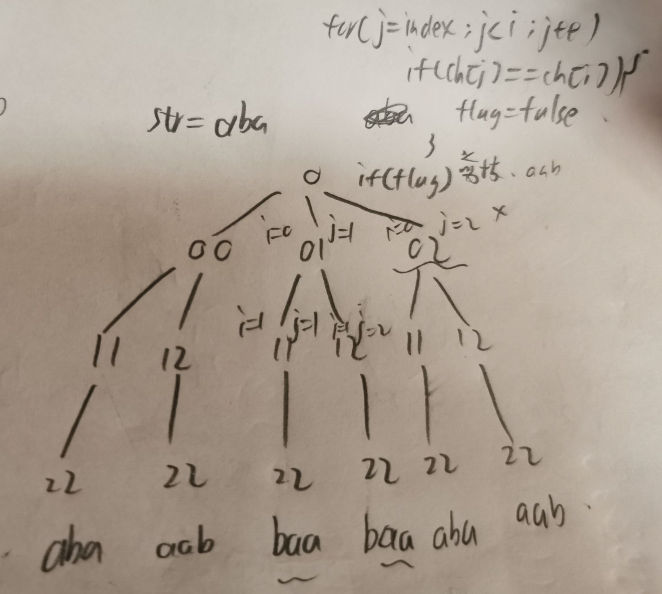
class Solution {
    public String[] permutation(String s) {
        char[] ch = s.toCharArray();
        ArrayList<String> list = new ArrayList<>();
        fun(list, ch, 0);
        return (String[])list.toArray(new String[0]);
    }

    public void fun(ArrayList<String> list, char[] chars,int index) {
        if (index == chars.length) {
            list.add(new String(chars));
        }
        for (int i = index; i < chars.length; i++) {
            boolean flag = true;
            //剪枝 （帅死了）
            for (int j = index; j < i; j++) {
                //含义：若是之前交换过得元素与当前交换得元素值若是一致，那么没有必要了
                if (chars[j] == chars[i]) {
                    flag = false;
                }
            }
            if (flag) {
                swap(chars, index, i);
                fun(list, chars, index + 1);
                swap(chars, index, i);
            }
        }
    }
    
    public void swap(char[] chars, int i, int j) {
        if (i != j) {
            char temp = chars[i];
            chars[i] = chars[j];
            chars[j] = temp;
        }
    }
}

2、优化点，可以将list集合优化为set。

括号生成【中等】

学习：leetcode题解

题目链接：22. 括号生成

题目内容：数字 n 代表生成括号的对数，请你设计一个函数，用于能够生成所有可能的并且 有效的 括号组合。

说明：递归的条件主要是围绕这括号的一个数量来进行决定的，不断往下递归，最终出口：left == n && right == n

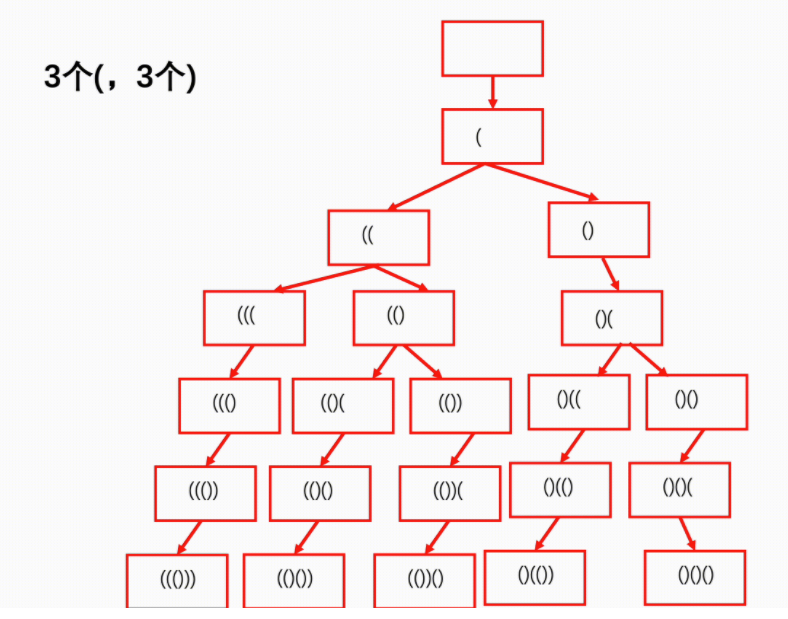
思路1：递归+回溯。【推荐】

• 通过利用StringBuilder来进行拼接，不会造成频繁创建字符串的情况。

复杂度分析：

• 时间复杂度：O(2^n^)
• 空间复杂度：O(n)

import java.util.*;


public class Solution {
    
    private ArrayList<String> res = new ArrayList<>();
    
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param n int整型 
     * @return string字符串ArrayList
     */
    public ArrayList<String> generateParenthesis (int n) {
        recursion(new StringBuilder(), 0, 0, n);
        return res;
    }
    
    public void recursion (StringBuilder str, int left, int right, int n) {
        //筛选条件
        if (left > n || right > n || left < right) {
            return;
        }
        //递归出口条件
        if (left == n && right == n) {
            res.add(str.toString());
            return;
        }
        //递归+回溯
        //递归(
        str.append('(');
        recursion(str, left + 1, right, n);
        str.deleteCharAt(str.length() - 1);
        //添加右边)
        str.append(')');
        recursion(str, left, right + 1, n);
        str.deleteCharAt(str.length() - 1);
    }
    
}

思路2：直接递归，无回溯。使用的是String字符串。

• 额外说明：在使用条件进行递归时，在最后进行回溯会出现问题！

复杂度分析：

• 时间复杂度：O(2^n^)
• 空间复杂度：O(n*2^n^)

import java.util.*;


public class Solution {
    
    private ArrayList<String> res = new ArrayList<>();
    
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     *
     * 
     * @param n int整型 
     * @return string字符串ArrayList
     */
    public ArrayList<String> generateParenthesis (int n) {
        recursion("", 0, 0, n);
        return res;
    }
    
    public void recursion (String str, int left, int right, int n) {
        //递归出口条件
        if (left == n && right == n) {
            res.add(str);
            return;
        }
        //递归(
        if (left < n) {
            recursion(str + '(', left + 1, right, n);
        }
        if (right < n && left > right) {
            recursion(str + ')', left, right + 1, n);
        }
    }
    
}

---

N皇后问题【中等】

题目链接：N皇后问题

题目内容：N 皇后问题是指在 n * n 的棋盘上要摆 n 个皇后，要求：任何两个皇后不同行，不同列也不在同一条斜线上，求给一个整数 n ，返回 n 皇后的摆法数。

思路1：递归，并利用集合容器来进行解决。

复杂度分析：

• 时间复杂度：O(n!)
• 空间复杂度：O(n)

import java.util.*;


public class Solution {
    
    private int result = 0;
    //使用三个容器
    Set<Integer> columns = new HashSet<>();//存储行号
    Set<Integer> posSet = new HashSet<>();//存储正对角线
    Set<Integer> conSet = new HashSet<>();//存储斜对角线
    
    /**
     * 
     * @param n int整型 the n
     * @return int整型
     */
    public int Nqueen (int n) {
        compute(0, n);
        return result;
    }
    
    //i表示行号、n表示边长
    //j就是列号，i-j就是斜号，i+j就是正斜
    public void compute(int i, int n) {
        if (i == n) {
            result++;
            return;
        }
        //全排列
        for (int j = 0; j < n; j++) {
            if (columns.contains(j) || posSet.contains(i - j) || conSet.contains(i + j)) {
                continue;
            }
            columns.add(j);
            posSet.add(i - j);
            conSet.add(i + j);
            //递归
            compute(i + 1, n);
            columns.remove(j);
            posSet.remove(i - j);
            conSet.remove(i + j);
        }
    }
    
}

思路2【推荐】：通过使用数组来进行解决，这里使用三个数组，同样分别对应上方的集合容器。

复杂度分析：

• 时间复杂度：O(n!)
• 空间复杂度：O(n)

import java.util.*;


public class Solution {
    
    /**
     * 
     * @param n int整型 the n
     * @return int整型
     */
    private int result = 0;
    //使用三个容器
    private boolean[] columns;
    private boolean[] posSet;//正斜线
    private boolean[] conSet;//反斜线
    
    /**
     * 
     * @param n int整型 the n
     * @return int整型
     */
    public int Nqueen (int n) {
        this.columns = new boolean[n];
        //开辟两倍的空间，足以为[0, 2 * n - 1]
        this.posSet = new boolean[n * 2];
        this.conSet = new boolean[n * 2];
        compute(0, n);
        return result;
    }
    
    //i表示行号、n表示边长
    //j就是列号，i-j就是斜号，i+j就是正斜
    public void compute(int i, int n) {
        if (i == n) {
            result++;
            return;
        }
        //全排列
        for (int j = 0; j < n; j++) {
            //注意是：j - i + n
            if (!columns[j] && !posSet[j - i + n] && !conSet[i + j]) {
                columns[j] = posSet[j - i + n] = conSet[i + j] =  true;
                compute(i + 1, n);
                //回溯
                columns[j] = posSet[j - i + n] = conSet[i + j] = false;
            }
        }
    }
}

矩阵中的最长自增路径【中等】

视频：LeetCode每日打卡.329.矩阵中的最长递增路径：特别清晰，看一遍就懂。

题目链接：矩阵最长递增路径

题目内容：给定一个 n 行 m 列矩阵 matrix ，矩阵内所有数均为非负整数。 你需要在矩阵中找到一条最长路径，使这条路径上的元素是递增的。并输出这条最长路径的长度。

思路1：采用记忆化dp+dfs来实现自增路径。

• dp中记录的是上下左右能够走的路径最大值。

import java.util.*;


public class Solution {
    
    private int[][] dp;
    private int res;
    
    /**
     * 代码中的类名、方法名、参数名已经指定，请勿修改，直接返回方法规定的值即可
     * 递增路径的最大长度
     * @param matrix int整型二维数组 描述矩阵的每个数
     * @return int整型
     */
    //核心：找到一条递增的路线，记录最长
    public int solve (int[][] matrix) {
        //初始化默认为0
        this.dp = new int[matrix.length][matrix.length];
        for (int i = 0; i < matrix.length; i++) {
            for (int j = 0; j < matrix[0].length; j++) {
                res = Math.max(res, dfs(i, j, matrix, Integer.MIN_VALUE));
            }
        }
        return res;
    }
    
    public int dfs(int i, int j, int[][] matrix, int prev) {
        //越界情况
        if (i < 0 || j < 0 || i >= matrix.length || j >= matrix[i].length) {
            return 0;
        }
        //若是当前值<prev值的话
        if (prev >= matrix[i][j]) {
            return 0;
        }
        //若是当前dp不为0时，直接返回
        if (dp[i][j] != 0) {
            return dp[i][j];
        }
        //当前未进行搜索情况
        dp[i][j] = 1;
        int up = dfs(i - 1, j, matrix, matrix[i][j]);
        int down = dfs(i + 1, j, matrix, matrix[i][j]);
        int left = dfs(i, j - 1, matrix, matrix[i][j]);
        int right = dfs(i, j + 1, matrix, matrix[i][j]);
        //拿的是当前的dp值以及上下左右能够递增的最大值来进行比较
        dp[i][j] = Math.max(dp[i][j], Math.max(Math.max(up, down), Math.max(left, right)) + 1);
        return dp[i][j];
    }
    
}

---

leetcode

79.单词搜索【中等】

题目链接：79. 单词搜索

题目内容：给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中，返回 true ；否则，返回 false 。

单词必须按照字母顺序，通过相邻的单元格内的字母构成，其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。

思路：

1、dfs深搜+回溯+剪枝

[[“o”,“a”,“a”,“n”],[“e”,“t”,“a”,“e”],[“i”,“h”,“k”,“r”],[“i”,“f”,“l”,“v”]]
[“oath”,“pea”,“eat”,“rain”]

复杂度分析：时间复杂度O(m.n.3^L^)，其中mn指的是对应矩阵的长宽，L指的是单词的长度；空间复杂度O(1)

class Solution {
    public boolean exist(char[][] board, String word) {
        char[] arr = word.toCharArray();
        for (int i = 0; i < board.length; i++) {
            for (int j = 0; j < board[i].length; j++) {
                if (dfs(board, arr, i, j, arr.length)) {
                    return true;
                }
            }
        }
        return false;
    }

    //进行深搜，限制的包含有字幕的长度
    public boolean dfs(char[][] board, char[] word, int i, int j, int k) {
        if (k == 0) {
            return true;
        }
        if (i < 0 || i >= board.length || j < 0 || j >= board[i].length ||  board[i][j] != word[word.length - k]) {
            return false;
        }
        //进行dfs
        board[i][j] = '1';
        //进行上下左右
        boolean res = dfs(board, word, i + 1, j, k - 1) || dfs(board, word, i - 1, j, k - 1) || 
                      dfs(board, word, i, j - 1, k - 1) || dfs(board, word, i, j + 1, k - 1);
        board[i][j] = word[word.length - k];
        return res;
    }
}