@[toc]

前言

除了去年11月份以及今年近几月的算法刷题之外，只有在当时20年蓝桥杯准备的时候才刷过一些题，在当时就有接触到一些动归、递归回溯、贪心等等，不过那会也还是一知半解，做的题目也特别少，因为考虑到之后面试有算法题以及数据结构算法对于一个程序员十分重要，我也开始了刷题之路。

我目前的学习数据结构与算法及刷题路径：

1、学习数据结构的原理以及一些常见算法。

2、代码随想录：跟着这个github算法刷题项目进行分类刷，在刷题前可以学习一下对应类别的知识点，而且这里面每道题都讲的很详细。

3、牛客网高频面试101题：牛客网—面试必刷101题，在刷的过程中可以在leetcode同步刷一下。

4、接下来就是力扣上的专栏《剑指offer II》、《程序员面试金典（第 6 版）》…有对应的精选题单来对着刷即可。

5、大部分的高频面试、算法题刷完后，就可以指定力扣分类专栏进行一下刷题了。

刚开始刷的时候真的是很痛苦的，想到去年一道题可能就需要好几小时，真的就很难受的，不过熬过来一切都会好起来，随着题量的增多，很多题目你看到就会知道使用什么数据结构或者算法来去求解，并且思考对应的时间空间复杂度，并寻求最优解，我们一起加油！

我的刷题历程

截止2022.8.18：

1、牛客网101题(其中1题是平台案例有问题)：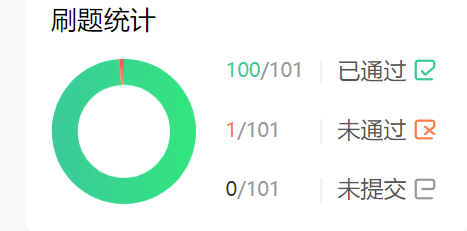

2、剑指offerII：

力扣总记录数：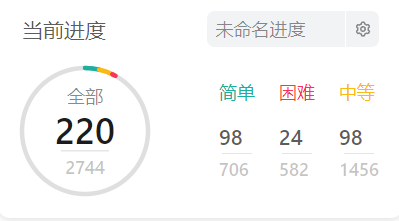

加油加油！

知识点

异或运算：能够快速找到差异。

• 看到加减法，可以想到使用异或操作。

①与加法相关联的情况
针对无进位的数字时，效果是相加，例如4 ^ 8 = 12
  0100
^ 1000
-------
  1100
若有进位，就是相减，例如：|5 ^ 7| = 2、|7 ^ 5| = 2
  101
^ 111
-----
  010

与运算：找到相同的元素值

①与加法相关联的情况
可匹配到进位位置，如5+7
 101
&111
-----
 101  此时你可以看到第一、三位都相同，正常加法的化，就需要进行进位了
 若是我们想要得到5+7的十位数，则表示(5 & 7) = 10，若是没有进位情况，那么就是0

剑指offer

剑指 Offer 15. 二进制中1的个数【简单】

题目链接：剑指 Offer 15. 二进制中1的个数

题目内容：编写一个函数，输入是一个无符号整数（以二进制串的形式），返回其二进制表达式中数字位数为 ‘1’ 的个数（也被称为 汉明重量).）。

思路：

1、右移+判断逻辑（超时）

复杂度分析：

• 时间复杂度：O(n)，这个n指的是n二进制的一个长度。
• 空间复杂度：O(1)

public class Solution {
    // you need to treat n as an unsigned value
    public int hammingWeight(int n) {
        int count = 0;
        while (n != 0) {
            if (n % 2 == 1) {
                count++;
            }
            //count += n & 1; //等同于上面
            n = n >> 1;
        }
        return count;
    }
}

2、进行与运算【目前最优】

复杂度分析：

• 时间复杂度：O(M)，这个M指的是二进制中1的数量。
• 空间复杂度：O(1)

public class Solution {
    // 示例：1001   ①1001 & 1000 => 1000。②1000 & 0111 => 0。也就是与的次数与1的个数相同。
    public int hammingWeight(int n) {
        int count = 0;
        while (n != 0) {
            count++;
            n = n & (n - 1);
        }
        return count;
    }
}

---

剑指 Offer 65. 不用加减乘除做加法【简单】

题目链接：剑指 Offer 65. 不用加减乘除做加法

题目内容：写一个函数，求两个整数之和，要求在函数体内不得使用 “+”、“-”、“*”、“/” 四则运算符号。

思路：

知识点：

异或：
针对相加无进位时，效果是相加，例如4 ^ 8 = 12
  0100
^ 1000
-------
  1100
若相加有进位时，就是相减，例如：|5 ^ 7| = 2、|7 ^ 5| = 2
  101
^ 111
-----
  010
结论：两数进行异或时，若是两个数字相加中无进位，那么结果就是相加；若是两个数字相加中有进位，结果就是相减【也就是非进位值】。
  
与运算：(a & b) << 1
 101
&111 
-----
 101 << 1 = 1010 
此时你可以看到第一、三位都相同，正常加法的化，就需要进行进位了
若是我们想要得到5+7的十位数，则表示(5 & 7) = 10，若是没有进位情况，那么就是0
结论：①两数进行与运算，可以得到同为1的位置，那这个位置表明是进位的位置。②与运算搭配<<左移，可以达到获取两个数字相加的进位值。
可匹配到进位位置，如5+7

简而言之：异或操作可以得到最终相加结果或两数的非进位值。与运算+右移操作可以得到整体的进位值，接着就可以进行下面求解了。

举例：a+b = 5 + 7 = 12

抓住 a ^ b   (a & b) << 1

①a = 5 = 101   b = 7 = 111
可拆成三步。
a ^ b = 2      a & b
 101             101
^111            &111
-----           -----
=010=2          =101 << 1 = 1010
接着(a & b)结果左移一位，取得进位制  (a & b) << 1 = 1010 = 10
可以看到当前 2 + 10 = 12，此时a = 2，b = 10

②a = 10   b = 1010
a ^ b = 8   (a & b) << 1 = 4，此时a=8,b=4
 0010       0010
^1010      &1010
------    -------
 1000 = 8   0010 << 1 = 0100 = 4

③a = 1000, b = 100
a ^ b = 12  (a & b) << 1 = 0，此时结束
 1000           1000
^0100          &0100
-----          ------
 1100 = 12      0000 << 1 = 00000 = 0
结束，求得值为12

1、位运算（异或和与运算搭配）

复杂度分析：时间复杂度O(1)，空间复杂度O(1)。

• 时间复杂度的最差情况下（例如 a =a= 0x7fffffff , b = 1b=1 时），需循环 32 次，使用 O(1)O(1) 时间；每轮中的常数次位操作使用 O(1)O(1) 时间。

迭代方式：

class Solution {
    public int add(int a, int b) {
        do {
            int num1 = a ^ b;
            int num2 = (a & b) << 1;
            a = num1;
            b = num2;
        }while (b != 0);
        return a;
    }
}

递归方式：

class Solution {
    public int add(int a, int b) {
        if (b == 0) {
            return a;
        }
        return add(a ^ b, (a & b) << 1);
    }
}

leetcode

338. 比特位计数【简单】

学习：leetcode题解、 清晰的思路—奇偶数求解

题目链接：338. 比特位计数

题目内容：给你一个整数 n ，对于 0 <= i <= n 中的每个 i ，计算其二进制表示中 1 的个数 ，返回一个长度为 n + 1 的数组 ans 作为答案。

速记：

①Brian Kernighan 算法，通过不断进行n & n-1求得为0过程的次数即为某个数的比特数。
②Brian Kernighan 算法进阶，每次求比特数时间复杂度为O(1)，核心就在于重复利用之前计算得到的比特数+1。
③奇偶判别，通过奇偶数之间的规律来进行求得比特数。
③将十进制数字转换为以字符串形式的二进制，接着将其中的0替换为空字符串，最后其长度即为比特数，空间复杂度最优。

思路：

1、Brian Kernighan 算法

思路：利用n & (n-1)来不断消解1，最终操作的次数即为一个数的比特数！

复杂度分析：时间复杂度O(nlogn)：遍历一遍需要n次，每个整数计算一个比特数最多不会超过logn次。空间复杂度O(1)：除了原本要返回的数组，其他仅为常数个。

class Solution {
    //Brian Kernighan 算法
    public int[] countBits(int n) {
        int[] nums = new int[n+1];
        for (int i = 1; i <= n; i++) {
            nums[i] = countOnes(i);
        }
        return nums;
    }

    /**
     * Brian Kernighan 算法的原理是：对于任意整数 xx，令 x=x & (x-1)x=x & (x−1)，
     * 该运算将 xx 的二进制表示的最后一个 11 变成 00。
     * 因此，对 xx 重复该操作，直到 xx 变成 00，则操作次数即为 xx 的「一比特数」。
     */
    public static int countOnes(int n) {
        int count = 0;
        while (n > 0) {
            n = n & (n - 1);
            count++;
        }
        return count;
    }
}

2、Brian Kernighan 算法（进阶）

思路：这里依旧使用的是Brian Kernighan 算法，只不过这里的话计算比特数的时间复杂度为O(1)，每个之后的比特数都会基于之前已经计算好的指定比特数+1.

代码：时间复杂度O(n)，空间复杂度O(1)

public int[] countBits(int n) {
    int[] nums = new int[n+1];
    for (int i = 1; i <= n; i++) {
        //每次基于之前计算好的比特数结果+1
        nums[i] = nums[i & (i-1)] + 1;
    }
    return nums;
}

3、奇偶数判别（位运算）

思路：奇偶数规律如下

奇数：前面的偶数+1
举例：1=>1  3(11)=>2  5(111)=>3
     0=>0  2(10)=>1  4(110)=>2 

偶数：与当前数/2的个数一样多
     2(10)=>1  4(100)=>1  6(110)=>2 8(1000)=>1
     1=>1      2(10)=>1   3(11)=>2  4(100)=>1

复杂度分析：时间复杂度O(n)，空间复杂度O(1)

//奇偶数判断
public int[] countBits(int n) {
    int[] nums = new int[n+1];
    for (int i = 1; i <= n; i++) {
        //位运算来判断奇偶数，若是==0则是偶数
        if((i & 1) == 0){
            nums[i] = nums[i/2];
        }else{
            nums[i] = nums[i-1] + 1;
        }
    }
    return nums;
}

4、字符串替换（空间最优）

思路：将数字转为二进制形式的字符串，将字符串中的0替换为空字符串，最后统计出来1的个数。

复杂度分析：时间复杂度O(nlogn)，空间复杂度O(1)

//字符串填充替换
public int[] countBits(int n) {
    int[] nums = new int[n + 1];
    for (int i = 1; i <= n; i++) {
        //将数字转为二进制形式的字符串，接着将0全部替换为空字符串，最终统计1的个数
        nums[i] = Integer.toString(i,2).replace("0","").length();
    }
    return nums;
}

461. 汉明距离【简单】

学习：leetcode题解

题目链接：461. 汉明距离

题目内容：

两个整数之间的 汉明距离 指的是这两个数字对应二进制位不同的位置的数目。

给你两个整数 x 和 y，计算并返回它们之间的汉明距离。

速记：

①先进行异或，接着使用JAVA内置的统计二进制中1的个数API。
②同样进行异或，统计1个数自己实现，使用Brian Kernighan 算法，不断进行n & n-1操作来进行统计。

思路：

1、内置计数功能（API）

思路：对于判断两个二进制为中不相同的位个数，我们可以使用异或操作，不相等的同一位置会被标为1，相等的则为0。之后对该二进制中1的个数进行统计即可。

复杂度分析：时间复杂度O(1)，空间复杂度O(1)

//异或之后求取数字二进制形式中1的个数
public int hammingDistance(int x, int y) {
    return Integer.bitCount(x ^ y);
}

2、Brian Kernighan 算法

思路：首先进行异或，接着使用Brian Kernighan 算法，不断对数字进行 n & n-1操作，直至=0，即可统计出该数字二进制形式1的个数、

复杂度分析：时间复杂度O(logn)，空间复杂度O(1)

class Solution {
    //Brian Kernighan 算法
    public int hammingDistance(int x, int y) {
        int s = x ^ y;//首先进行异或
        int count = 0;
        while (s > 0) {
            s = s & (s - 1);
            count++;
        }
        return count;
    }
}